压缩感知、稀疏傅里叶变换

1、什么是压缩感知

　　也叫压缩采样，稀疏采样，压缩传感。是通过开发信号的稀疏特性，在远小于奈奎斯特采样率的情况下，用随机采样获取信号的离散样本，然后通过非线性重建算法完美重建的信号。

2、核心思想

　　第一个就是信号的稀疏结构。传统的shannon信号表示方法只利用了信号的带宽。但是在现实生活中，信号本身还有一些结构特点，相对于信号带宽的自由度，这些结构特点是由信号更小的一部分自由度所决定。换句话说就是在信号损失较小的情况下，这种信号可以用很少的数字编码表示。（压缩编码？类似于压缩文件，用较少的彪马表示原本来的信息，只要不影响使用就好啊）。

　　第二个就是不相关特性。稀疏信号的有用的信息获取是通过一个非自适用的采样方法将信号压缩成较小的样本数据来完成的。

　　理论证明压缩感知的采样方法只是一个简单的将信号与一组确定的波形进行相关conv的操作（这就是类似脉冲压缩？匹配滤波？）

　　压缩感知抛弃了当前采样信号中的冗余信息。

　　从连续时间信号------》 压缩样本------》数字信号处理（最优方法--已知信号稀疏的欠定线性逆问题）

　　雷达成像在雷达领域的应用与传统雷达成像技术相比，它实现了两个重要改进: 在接收端省去脉冲压缩匹配滤波器; 同时由于避开了对原始信号的直接采样, 降低了接收端对模数转换器件带宽的要求. 设计重点由传统的设计昂贵的接收端硬件转化为设计新颖的信号恢复算法, 从而简化了雷达成像系统。

　　　

　　压缩感知高速我们：如果信号在某一个正交空间具有稀疏性（稀疏就是间隔比较大，可以压缩）就能够以较低的采样率实现采样过程替代接收端的匹配滤波。

 

 

 

 

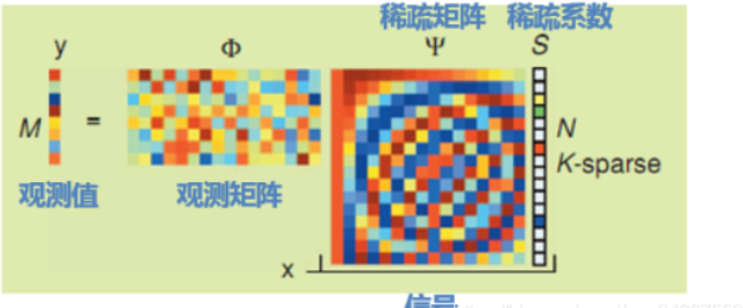
一般的，压缩感知的数学公式为

                                                        y=Φx

其中 y 是观测值，也就是我们随机的采样值， 而Φ 是观测矩阵，也就是我们采样的规则， x 是我们的原始信号。
从这个公式我们来理解压缩感知。
从右到左，是采样的过程，已知 Φ 和 x 求解 y  ,对于原始信号，我们通过观测矩阵所描述的观测（采样）方式，从而获得了观测值（采样值）。当我们处理信号为稀疏信号时，那么便可以保证在采样阶段，观测值的数据量是远小于原始信号。
而从左到右，就是重构的过程，已知 y和 Φ 求解 x 。

而在实际中，我们的信号 x xx 往往并不稀疏，那么此时便对其进行处理，使其变得稀疏，比如进行正交变换，
　　　　　　　　　　x = Ψ s x 
　　　　　　　　　　x=Ψs

最后的推导：原文链接：https://blog.csdn.net/qq_34687559/article/details/112915999