exKMP

类似于 马拉车 的思想，利用之前的已知的信息推出当前的答案。

P5410 【模板】扩展 KMP/exKMP（Z 函数）

一个串的每个后缀与另一个串的最长公共前缀。

S==T时

类似于马拉车算法，红色块为右端点最右的后缀。

1. 当前位置为最右边之后，串未知，暴力更新。

2. 当前位置未超右端点，答案与左边第二个橙色块的答案一样

3. 当前位置后超最右边，在左边橙色块基础上暴力拓展

S!=T时

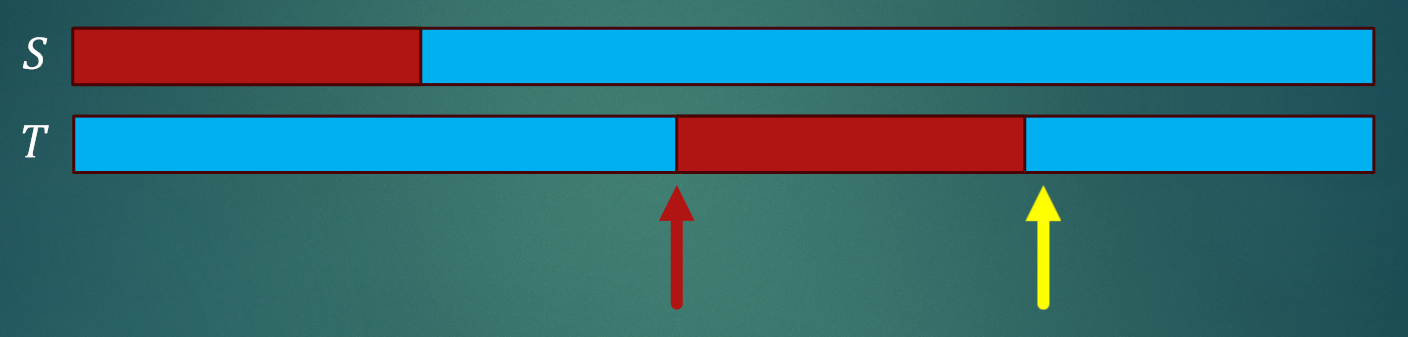
1. 超过最右边，未知，暴力枚举。

2. 未超最右边，黄块与第二个橙色块的一样，第二个橙色块与第一个橙色块一样，所以还是要单独算S串自己的每个后缀的最大公共前缀。

3. 超右端点，在获得答案的基础上向右暴力拓展。

因为两部分操作相同，可以写成一个函数进行操作。

#include<bits/stdc++.h>
#define ll long long
#define int ll
using namespace std;
const int N=2e7+10;

char s[N],t[N];
int anss[N],anst[N];

void exkmp(char *a,char *b,int *ansa,int *ansb){
	int n=strlen(a+1);
	for(int i=1;i<=n;i++){
		ansa[i]=0;
	}
	
	int p=1;
	if(a+1==b+1){
		p=2;
		ansa[1]=n;
	}
	 
	int l=0,r=0;
	for(int i=p;i<=n;i++){
		if(i<=r){
			ansa[i]=min(ansb[1+i-l],r-i+1);	
		}
		while(i+ansa[i]<=n&&b[1+ansa[i]]==a[i+ansa[i]]) ansa[i]++;
		if(i+ansa[i]-1>r){
			l=i;
			r=i+ansa[i]-1;
		} 
	}
}

void solve(){
	cin>>t+1>>s+1;
	
	exkmp(s,s,anss,anss);
	exkmp(t,s,anst,anss);
	
	int ans=0;
	for(int i=1;i<=strlen(s+1);i++){
		ans^=i*(anss[i]+1);
	}
	cout<<ans<<"\n";
	ans=0;
	for(int i=1;i<=strlen(t+1);i++){
		ans^=i*(anst[i]+1);
	}
	cout<<ans<<" ";
}
signed main(){
    ios::sync_with_stdio(0);
    cin.tie(nullptr);
    int t=1;
    while(t--){
        solve();
    }
    return 0;
}