组合数学

格子计数

从坐标 \((0,0)\) 出发，每次可以向上向右走一格，求走到 \((n,m)\) 位置的方案数。

通常情况下可以用 dp，我们答案也可以是 \(\binom{n+m}{n}\)，意思是总共 \(n+m\) 步选 \(n\) 步向上走其他向右走的方案数。

合法括号数

在长度为 \(2n\) 的括号序列中合法括号序列个数，合法括号为任意前缀左括号数量大于右括号数量，整个序列左括号和右括号数量相同。

可以想到可以用操作来形容括号，向上就是右括号，向右就是左括号，我们不合法的操作是碰触到直线 \(y=x+1\)，我们把之后的操作进行折叠那最终不合法的点一定会到达点 \((n-1,n+1)\)。

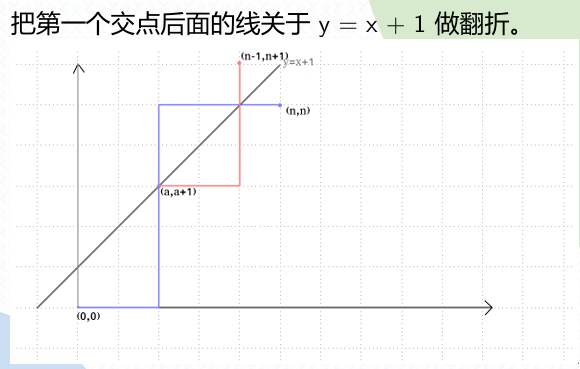
于是我们就得到结论：到达点 \((n-1,n+1)\) 的方案数恒穿过直线 \(y=x+1\)，故是不合法括号序列数量。

总方案数减去不合法方案数就是合法括号序列方案数。

int fac[N]={1,1};
int c(int a,int b){
	return fac[a]/fac[b]/fac[a-b];
}
signed main(){
	int n=4;
	for(int i=2;i<N;i++){
		fac[i]=fac[i-1]*i%mod;
	}
	cout<<c(2*n,n)-c(2*n,n+1)<<" ";
	a[0][0]=1;
	for(int i=0;i<=n;i++){
		for(int j=0;j<=n;j++){
			if(j<i) continue;
			a[i][j]+=a[i-1][j]+a[i][j-1];
		}
	}
	cout<<a[n][n];
    return 0;
}

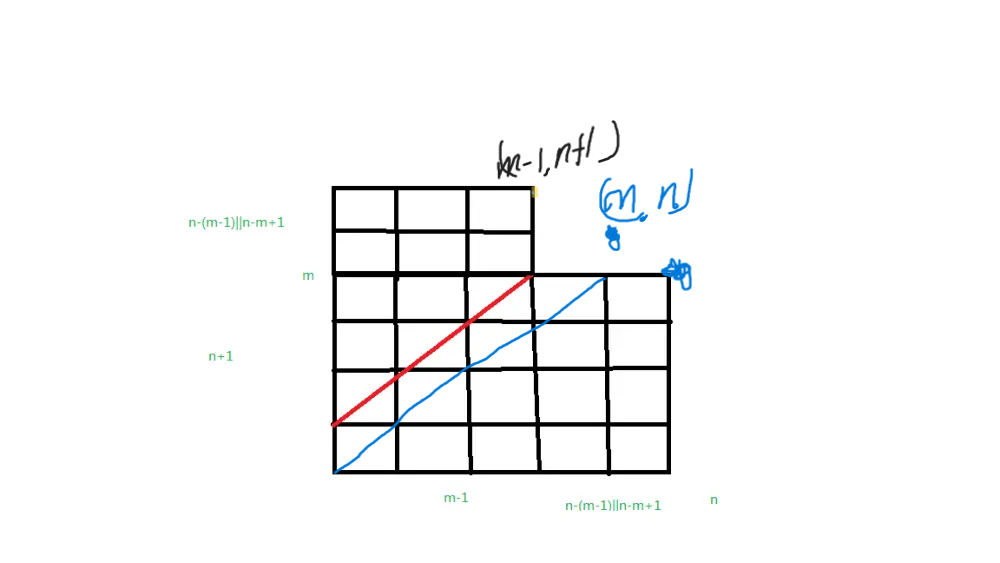
P1641 [SCOI2010] 生成字符串

和上面同样做法，不过注意我们是按照红线路径对折，\(x,y\) 要互换后平移。

#include <bits/stdc++.h>
#define ll long long
#define int ll
#define ls p<<1
#define rs p<<1|1 
#define re register 
#define pb push_back
#define pir pair<int,int>
#define f(a,x,i) for(int i=a;i<=x;i++)
#define fr(a,x,i) for(int i=a;i>=x;i--)
#define lb(x) x&(-x); 
using namespace std;
const int N=2e6+10;
const int M=8e6+10;
const int mod=20100403;
int n;
 
int fac[N];
int inv[N];
int ifac[N];
 
int c(int a,int b){
	return fac[a]*ifac[b]%mod*ifac[a-b]%mod;
}
signed main(){
    ios::sync_with_stdio(0);
    cin.tie(nullptr);
	int n,m;
	cin>>n>>m;
	fac[0]=fac[1]=1;
	inv[0]=inv[1]=1;
	ifac[0]=ifac[1]=1;
	for(int i=2;i<N;i++){
		fac[i]=fac[i-1]*i%mod;
		inv[i]=inv[mod%i]*(mod-mod/i)%mod;
        ifac[i]=ifac[i-1]*inv[i]%mod;
	}
	cout<<(c(n+m,n)-c(n+m,n+1)+mod)%mod;
    return 0;
}