【题解】P5787 二分图 /【模板】线段树分治

二分图最简单的方法是染色法实现，但是扩展域并查集也可以实现，有两个集合 \(S,T\)，具体的是相连边的两个点 \(x,y\) 总是在不同的两个集合中，若出现在同一集合中即不是一个二分图。

对于时间段建边考虑用线段树储存，线段树按照时间轴划分，将将对应时间区间的节点储存上当前连边操作，小时间区间总是被大时间区间包含。

大佬的图。

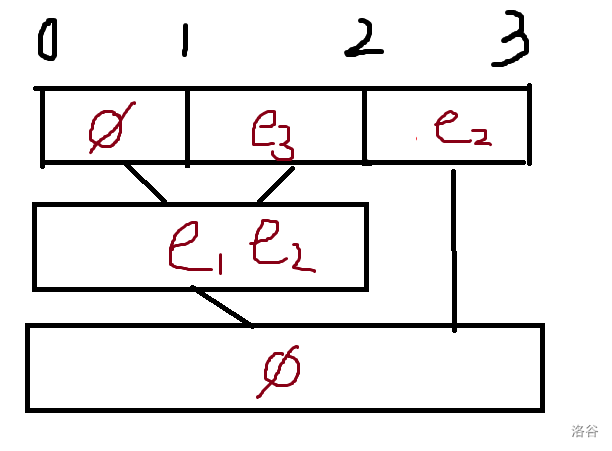
可以看到 \(e_2\) 这个操作在互不相交的对应时间区间上都储存了，我们如何查询呢，我们从大区间依次加边，同时判断合法，如果[l,r]这个区间出现不合法的情况，我们输出 \(r-l+1\) 次 NO 并且他之后的小区间也不用遍历加边了，直接返回，否则直到叶子节点时输出 YES。

当然返回要撤销对应的加边操作，我们用可撤销并查集，用栈储存当时的状态，不断回溯。

#include <bits/stdc++.h>
#define ll long long
#define int ll
#define ls p<<1
#define rs p<<1|1 
#define re register 
#define pb push_back
#define pir pair<int,int>
#define f(a,x,i) for(int i=a;i<=x;i++)
#define fr(a,x,i) for(int i=a;i>=x;i--)
#define lb(x) x&(-x);
const int N=6e5+10;
const int mod=1e9+7;
using namespace std;

int n,m,k;
int u[N],v[N];
vector<int> t[N];
int fa[N],siz[N];
stack<pir> s;

int find(int x){
	while(x^fa[x]){
		x=fa[x];
	}
	return x;
}

void change(int p,int pl,int pr,int id,int l,int r){
	if(pl>=l&&pr<=r){
		t[p].push_back(id);
		return;
	}
	int mid=(pl+pr)>>1;
	if(l<=mid){
		change(ls,pl,mid,id,l,r);
	}
	if(r>mid){
		change(rs,mid+1,pr,id,l,r);
	}
}

void merge(int x,int y){
	if(x==y){
		return;
	}
	if(siz[x]>siz[y]){
		swap(x,y);
	}
	s.push({x,siz[x]==siz[y]});
	fa[x]=y;
	siz[y]+=(siz[x]==siz[y]); 
}

void solve(int p,int l,int r){
	int ok=1;
	int si=s.size();
	for(int i=0;i<t[p].size();i++){
		int id=t[p][i];
		int x=find(u[id]),y=find(v[id]);
		if(x==y){
			for(int j=l;j<=r;j++){
				cout<<"No\n";
			} 
			ok=0;
			break;
		}
		merge(find(u[id]+n),y);
		merge(find(v[id]+n),x);
	}
	if(ok){
		if(l==r){
			cout<<"Yes\n";
		}
		else{
			int mid=(l+r)>>1;
			solve(ls,l,mid);
			solve(rs,mid+1,r); 
		}
	}
	while(s.size()>si){
		int x=s.top().first;
		siz[fa[x]]-=s.top().second;
		fa[x]=x;
		s.pop();
	}
}

signed main(){
//	freopen("xp1.in","r",stdin);
    ios::sync_with_stdio(0);
    cin.tie(nullptr);
	cin>>n>>m>>k;
	
	for(int i=1;i<=m;i++){
		int l,r;
		cin>>u[i]>>v[i]>>l>>r;
		if(l^r){
			change(1,1,k,i,l+1,r);
		}
	}	
	for(int i=1;i<=n;i++){
		fa[i]=i,siz[i]=1,fa[i+n]=i+n;
	}
	solve(1,1,k);
	return 0;
}