【题解】P4688 [Ynoi2016] 掉进兔子洞

洛谷 P4688 [Ynoi2016] 掉进兔子洞

莫队配合 bitset 例题。

lxl 官方题解。

https://olddrivertree.blog.uoj.ac/blog/4690

想到如果只有每个数只出现一次怎么做，可以莫队移动区间用 bitset 维护每个数的是否出现，再对 \(3\) 个区间进行与操作就是交集出现的数。

但是这只能求出数字出现种类数而不是数字出现个数。

但是 bitset 也可以维护出现个数，因为序列长度为 \(n\)，所以所有数的总出现次数也只有 \(n\)，我们继续不去重的离散化，对于每个数表示的是比他小的个数，这在 bitset 上相当于一个下标，之后的数 \(cnt[x]\) 个都是他的位置，每次莫队拓展时在最后位置添加，其他的就和普通没区别了。

注意：拓展时先扩大再缩小，不然等着 RE 吧。

官方题解图：

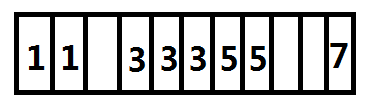
因为我们没法存下 \(3\times 10^5\) 个 \(1\times 10^5\) 的 bitset 所以考虑分组莫队。

#include <bits/stdc++.h>
#define int long long
#define ls p<<1
#define rs p<<1|1 
#define re register 
#define pir pair<int,int>
const int N=1e5+10,M=25005;
const int mod=1e8;
using namespace std;
 
int n,m;
int a[N],b[N];
int of[N],len;
 
struct ss{
	int id,l,r;
}q[N<<2];
 
int ans[N];
 
bool cmp(ss g,ss h){
	return (of[g.l]^of[h.l])?of[g.l]<of[h.l]:(of[g.l]&1)?of[g.r]<of[h.r]:of[g.r]>of[h.r];
}
 
bool vis[M];
int cnt[N];
bitset<N> s,sum[M];
 
void add(int x){
	x=a[x];
	cnt[x]++;
	s[x+cnt[x]-1]=1;
}
void del(int x){
	x=a[x];
	s[x+cnt[x]-1]=0;
	cnt[x]--;
}
 
void solve(int k){
	
	int tot=0;
	memset(vis,false,sizeof vis);
	memset(cnt,0,sizeof cnt);
	memset(ans,0,sizeof ans);
	s.reset();
	
	for(int i=1;i<=k;i++){
		for(int j=1;j<=3;j++){
			tot++;
			q[tot].id=i;
			cin>>q[tot].l>>q[tot].r;
			ans[i]+=q[tot].r-q[tot].l+1;
		}
	}
	
	sort(q+1,q+1+tot,cmp);
	
	int l=1,r=0;
	
	for(int i=1;i<=tot;i++){
		int ql=q[i].l,qr=q[i].r,id=q[i].id;
		while(l>ql) add(--l);
		while(r<qr) add(++r);
		while(l<ql) del(l++);
		while(r>qr) del(r--);
		
		if(!vis[id]){
			sum[id]=s;
			vis[id]=1;
		}
		else{
			sum[id]&=s;
		}
	}
	
	for(int i=1;i<=k;i++){
		ans[i]-=sum[i].count()*3;
		cout<<ans[i]<<"\n";
	}
}
 
 
signed main(){
//	freopen("xp1.in","r",stdin);
    ios::sync_with_stdio(false);
    cin.tie(nullptr); 
    
    cin>>n>>m;
    
    len=sqrt(n);
    
    for(int i=1;i<=n;i++){
    	cin>>a[i];
    	b[i]=a[i];
    	of[i]=(i-1)/len+1;
	}
    sort(b+1,b+1+n);
    for(int i=1;i<=n;i++){
    	a[i]=lower_bound(b+1,b+n+1,a[i])-b;
	}
    int T=M-5;
    while(m){
    	if(m<=T){
    		solve(m);
    		break;
		}
		else{
			solve(T);
			m-=(T);
		}
	}
	return 0;
}