题解集

代码暂时还没爬到，题目的中文部分有些乱码，不过题号还是看的清楚的

AGC005D

问满足对于所有的 \(i\) 都有 \(|P_i-i|\neq k\) 的排列 \(P\) 的个数。 \(n\le 2000\)。

正着不好求，那我直接容斥，用 \(f(i)\) 来表示钦定至少 \(i\) 个地方冲突的方案数。答案就是 \(\sum_{i=1}^n (-1)^i \times f(i)\)。

我们看到一个点 \(x\) 和位置 \(x± k\) 有关系，我们可以抽象看做边，这样可以把原序列分成若干条链（链中一半是点一半是位置）。

这里偷一张 ez_lcw 巨佬的图方便理解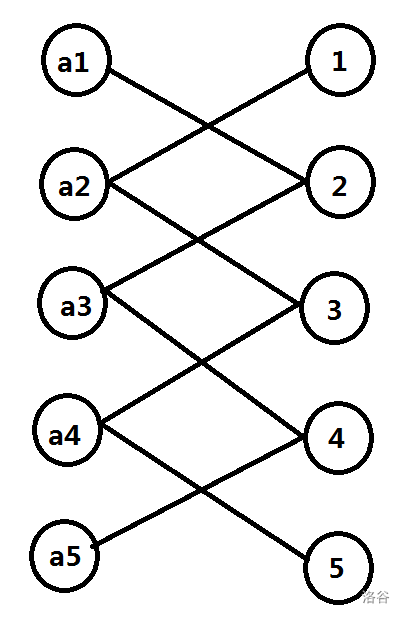

这里可以分成 两条路。

其一 \(dp\):

我们可以对每一个链分别考虑： \(f[i][j][0/1]\) 表示前 \(i\) 个节点选了 \(j\) 个边且，第 \(i\) 节点和 \(i-1\) 节点是否连边的方案数。有：

\[f[i][j][0]=f[i-1][j][0]+f[i-1][j][1] \]

\[f[i][j][1]=f[i-1][j-1][0] \]

在实现的时候可以把所有链首尾相接一起处理（但是这样新链的起点无法向旧链的终点连边），最终就有 \(f(i)=(n-i)!\times f[2n][i]\)。（因为 \(i\) 是钦定的，所以剩下的随便选）。

其二卷积：

我们知道对于每一个节点数为 \(m\) 的链取 \(i\) 个互不相邻的边的方案数是 \(\dbinom{m-i}{i}\)。（类似于隔板法）。每个链方案独立的，把所有链的 OGF 卷积起来即可。如果用的是暴力卷积 是 \(\mathcal{O}(n\times \frac{n}{k} \times k)\) 的，如果用多项式科技加速可以到 \(\mathcal{O}(n\log n)\)。

这里给出一个暴力卷积的核心代码：

CF852I

题意：

给定 \(n\) 个节点的树，每个节点有一个男生和女生。每个人都有一个喜欢的数字。

然后 \(m\) 次询问，每次询问树上从 \(a\) 到 \(b\) 的路径中，有多少对男女喜欢的数字相同。

\(n,m\leq 10^5\)。

树上序列询问，可以考虑树上莫队， \(n,m\) 在 \(10^5\) 根号算法完全能过。

由于 这个题SP10707 才是树上莫队“公认”的板子题，本题直接套用模板即可，所以本题解里将会略去对模板的解释。

要求多少对男女喜欢的数字相同，要男女分开记录，分开算。

记录男和女分别喜欢某个数字的人数，当加入一个点时，答案增加该点异性相同数字的人数，删除时，答案减少该点异性相同数字的人数。

核心代码：（板子略去）

CF852G

神仙 SharpnessV 的字典树题解中做法过于复杂了，活活把这个 1700 的题恶评到了紫。

题意：

求 \(n\) 个字符串中能与一个至多带三个 ? 的字符串匹配的数量。

其中 ? 可以代表任意一个字符或者空字符，其中字符串中只会出现 \(a,b,c,d,e\) 这五个字符。

根据计算，三个 ? 能玩出的花样只有至多 \(6^3\) 种，直接枚举出所有可能性和这些字符串的 $\rm hash $ 值，然后匹配一下即可。

其中要注意的是 若有连续两个 ? 可能会出现重复计算贡献的情况，这里要特判一下去个重。

由于cf可以 \(\rm hack\)，这里的时间不是卡的很紧，那么直接把字符串用 std::string 的形式丢到 map 里面就既方便又不用怕 \(\rm hash\) 碰撞了。

核心代码：

CF852F

题意：

有一个长度为 \(n\) 的数组全部元素都是 \(a\) 。

现在进行 \(m\) 次操作，每次操作将 \(A[i]\) 变为 \(A[i]*A[i+1]\) ，最后一个元素不变。

现给出 \(n,m,a,Q\)，输出 \(m\) 次操作后的 \(A\) 数组，每个元素对 \(Q\) 取模。

\(n,m\leq 10^6+123\) 。

这个题的操作不算复杂，而且给出的初始数组元素种都是 \(a\) ，可以看出来是让我们直接计算出每一位的值

$ a^1 \ a^1 \ a^1 \ a^1 \ a^1 \ a^1 \ a^1$

\(a^2 \ a^2 \ a^2 \ a^2 \ a^2 \ a^2 \ a^1\)

\(a^4 \ a^4 \ a^4 \ a^4 \ a^4 \ a^3 \ a^1\)

\(a^8 \ a^8 \ a^8 \ a^8 \ a^7 \ a^4 \ a^1\)

\(a^{16} \ a^{16} \ a^{16} \ a^{15} \ a^{11} \ a^5 \ a^1\)

\(…\)

如果不是最后一个数的“干扰” \(m\) 次过后应该会变成 \(a^{(2^{m-1})}\)，但是最后一个元素始终是 \(a\) ，所以我们提取出每一位数的指数与 \({2^{m-1}}\) 的差值，为了方便找规律，我们再把序列反转，可以得到：

\(0 \ 0\ 0\ 0\ 0\ 0 \ 0…\)

\(1 \ 0\ 0\ 0\ 0\ 0 \ 0…\)

\(3 \ 1\ 0\ 0\ 0\ 0 \ 0…\)

\(7 \ 4\ 1\ 0\ 0\ 0 \ 0…\)

\(15 \ 11\ 5\ 1\ 0\ 0 \ 0 …\)

\(31 \ 26\ 16\ 6\ 1\ 0 \ 0 …\)

\(61 \ 57\ 42\ 22\ 7\ 1\ 0 …\)

\(…\)

可以看出来是类似杨辉三角形式的，一个数是上面相邻两数之和，每行第一个数是 \(2^{i-1}-1\) ，每行最后一个不是零的数是 \(1\) 。

由于 \(n,m\) 是 \(10^6\) 级别的，所以不能爆算每一位的值，需要找到捷径。

再对这个数列取一个差分（就是后面的一位减去前面的一位），得到如下的东西。

\(0 \ 0\ 0\ 0\ 0\ 0 \ 0…\)

\(1 \ 0\ 0\ 0\ 0\ 0 \ 0…\)

\(2 \ 1\ 0\ 0\ 0\ 0 \ 0…\)

\(3 \ 3\ 1\ 0\ 0\ 0 \ 0…\)

\(4 \ 6\ 4\ 1\ 0\ 0 \ 0 …\)

\(5 \ 10\ 10\ 5\ 1\ 0 \ 0 …\)

\(6 \ 15\ 20\ 15\ 6\ 1\ 0 …\)

\(…\)

这就十分的眼熟了，第 \(i\) 行 第 \(j\) 列竟是 \(\tbinom{i-1}{j}\)。

但还有个问题：这里我们求的是指数上的数，这个问题的数规模会很大，要用为指数取模，这里不必用到欧拉定理，只要枚举出 \(a^i \mod Q=1\) 的 \(i\) 即可，由题意得，这个 \(i\) 也是 \(10^6\) 级别的，然后指数都对这个 \(i\) 取模即可。

核心代码：

\u9898\u89e3 CF852C

题意：

有一个正 \(2n\) 边形，在每条边上有 \(n\) 等分点。现在已经选定了 \(n\) 个点，第 \(i\)个点分别位于第 \(2i+1\) 条边上，且这 \(n\) 个点的序号构成了一个排列；你需要再选出 \(n\) 个点位于第 \(2i\) 条边上，并且这 \(n\) 个点的序号也构成一个排列，使得这些点构成的多边形面积最大。

这是个和几何略相关的题，简略作一个角的图，设左边的取到 \(i\) 等分，右边的取到 \(j\) 等分，中间的取到 \(x\) 等分，设两遍之角的补交为 \(\theta\)。

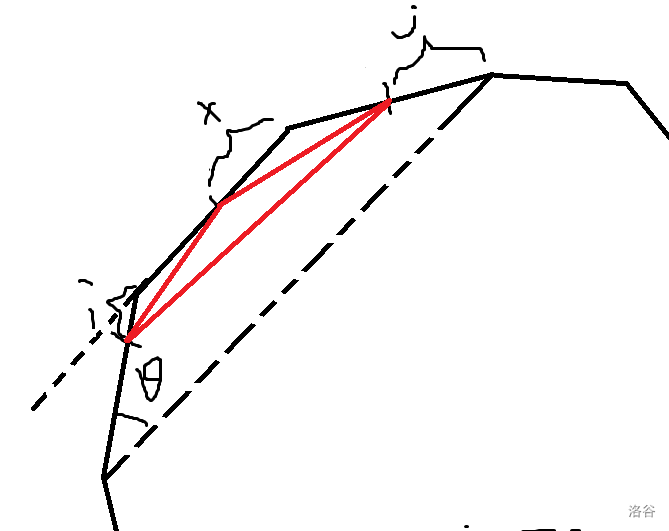
那么红色部分的面积为 $(L-j+i)\cos \theta \times (L-j+i)\sin \theta-x(L-j)\sin \theta -(L-x)i\sin\theta $

刨去前面和 \(x\) 无关的部分，留下 \(\sin \theta (-Lx-Li+x(i+j))\) 要使这个最大，只要大的 \(x\) 匹配大的 \((i+j)\) 即可，排序一下就好了。

核心代码

CF833C 2700

这就是 CF 评分 2700 的题吗，还真是有够好笑的呢

题意：

对一个数进行操作把这个数字按照不降序进行排列，之后把所有的前导零去掉。

对 \([L,R]\) 里的数都进行操作，最后能得到多少不同的数。

\(1\leq L,R\leq 10^{18}\)

模拟赛上遇到了，秒了，没发现是之前做过的题，这个题也没加入我的刷题纪录里，看到了还没有题解就来写一篇。

首先看到对 \([L,R]\) 里所有数计数可以直接想到数位 \(\rm dp\) ，但是这个题最后的计数要重排过并且不能只是单纯的 \(work(R)-work(L-1)\) 这样减去贡献，要计算的是去重后的数量。

再来思考一下操作过后会得到的数字，是一个单调不降没有前导零的数，这样的数在 $[1,10^{18}] $ 中有多少呢？

暴力 \(dfs\) 一下就可以知道 ，大概在 \(10^6\) 量级内，那么我们只要遍历所有的可行的答案然后判断一下是否可以重排得到一个在 \([l,r]\) ，这个是 \(O(\log n)\) 的模拟一下就好了。

代码：（比赛时写的又臭又长）

CF847L Berland SU Computer Network

题意：

给你一个无根树中每个节点有多少儿子和每个儿子子树中包含那些节点。（用 - 来分隔各个儿子）。

要求你输出这个树，或者指出不存在这样的树。

\(n \leq 10^3\)。

一道比较简单的构造题。既然给出了每个儿子所在子树的节点。那么我们可以直观考虑从简单处入手。

什么最简单？叶子节点，如果一个节点是叶子节点，那么这个节点只有一个儿子（无根树），这样就可以把一个叶子节点抽出来了。

抽出来之后，自然是找道一个节点与他相连然后连边。这个节点处理好了，信息也没用了之后把这个叶子删掉，这样又会有新的叶子出现，过程类似于拓扑排序，可以用队列实现。

处理结果是否合法也是一个要点，如果少考虑不合法情况容易被卡掉。（这里默认大家都会处理输入）。

核心代码：

\u83dc\u903c\u53ea\u914d\u7ed9\u6c34\u9898\u5199\u9898\u89e3 \u4e4b CF847K

题意：

有 \(n\) 次旅行计划，一次单程旅行的车费为 \(a\)，代表从下车的地方上车再到另一个地点的花费为 \(b\)，

按照题意模拟每一条路线上的花费，然后排序，优先对花费多的路线使用特价券。

题目中给的使站点的名字，可以直接用 string 存然后丢到 map 里就好了。

核心代码：

CF847J Students Initiation

题意：

有 \(n\) 个人， \(m\) 对关系，要求每对关系中，有且仅有一个人给另外一个人送礼物，并且使送出礼物最多的人送的礼物尽可能少。并输出送礼物的方案。

\(n\leq 5000\)。

由于瞄了一眼 cf 的原题 ，看到 flow 就没怎么想直接秒了，感觉可能浪费一道好题…

「最多的最少」 可以让我们想到二分答案，二分这个 「最少」 值。

那么二分出这个 「最少」 值 \(x\) 后，直接从源点向所有的点连 \(x\) 流量的边。表示这个点最多给出 \(x\) 个礼物。

然后把每个点拆成出入两个点，每一个关系连一个双向的边，出的点连汇点。但是如果 \((a,b)\) 有边，不能出现 $a\to b $ 且 $b\to a $ 的情况，所以再搞一个限制把这个双向的边限制只有一个方向。

判断是否可行只要看是否流满即可。

核心代码：（网络流部分略去）

\u83dc\u903c\u53ea\u914d\u7ed9\u6c34\u9898\u5199\u9898\u89e3 \u4e4b CF847I

题意：

给一个 \(n\times m\) 的方格和 \(q,p\) 的值。

其中 . 表示不产生噪音但可以传播的格子。* 表示不产生噪音也不会传播噪音的格子。A~Z 表示产生噪音的方格 ，产生 \((X-'A'+1)*q\) 的噪音（A 表示 \(q\)，B 表示 \(2*q\) … Z表示 \(26*q\)）。

噪音可以向四个方向传播，每经过一个格子就会减半（向下取整），同一个噪声源对于一个格子产生的传播不叠加。

问最后有多少格子的噪声的值大于 \(p\)。

简单模拟题，直接对于每个点 \(\rm bfs\) 即可。注意，影响的距离要用的最短。

代码有点冗长但是十分的基础：

\u83dc\u903c\u53ea\u914d\u7ed9\u6c34\u9898\u5199\u9898\u89e3 \u4e4b CF847H

题意：

给一个数组，问多少次对单个位置 \(+1\) 操作后，能将序列变成一段严格递增的之后严格递减。

\(n\leq 10^6\) 。

枚举每一个点，计算以这个点为转折点的修改花费。

可以预处理出一段前缀成为单调递增的最小花费。

同理可以预处理出一段后缀成为单调递减的最小花费。

核心代码：

\u83dc\u903c\u53ea\u914d\u7ed9\u6c34\u9898\u5199\u9898\u89e3 \u4e4b CF847F

题意：

\(m\) 个人给 \(n\) 个候选人投票，票数前 \(k\) 的候选人可以被选中，若票数相同则最后一票的时间早的人在前，无票者不能被选中。

已知前 \(a\) 个人的投票，问 \(n\) 个候选人是下面三种情况的哪种。

无论剩下的 \(m-a\) 人选谁，都能被选中。

有机会被选中。

无论剩下的 \(m-a\) 人选谁，都不能被选中。

\(n,m\leq 100\) 。

对于 \(1\) ，尽量分配票给当前选手后的第一位，最后是否能被挤出前 \(k\) 。

对于 \(3\) ，剩余票全部分配给自己，最后是否能进入前 \(k\) 。

若不是 \(1\) ， \(3\) 那么就是 \(2\) 。

由于数据范围较小，直接模拟即可。

核心代码：

\u83dc\u903c\u53ea\u914d\u7ed9\u6c34\u9898\u5199\u9898\u89e3

题意：

构建一个规则的括号序列，使得它恰好含有 \(n\) 对括号并且恰好含有 \(k\) 对嵌套，或输出 Impossible 。（一对嵌套表示两对对应的括号一个被另一个包含）。

\(n\leq 10^5\)。

先确定一个上限，比较显然：这样排列 \(((((…))))\) 就可以搞到最多的括号嵌套。这样得到的上限是 $k\leq \frac{n\times(n-1)}{2} $ 才可以有解。

可以证明，没有其他方案可以得到更多的嵌套。

那么思考另一个问题：是否小于上限的 \(k\) 都一定有解，且如何构造。

对于 \(((((…))))\) 的括号序列，只要将里面某的一对 \(()\) 向外边提出 \(i\) 对 \(()\) 即可使得嵌套的数量减少 \(i\)。那么这样就可证明可以构造出的答案范围是稠密的。

知道了这些，正着构造用递归算法即可。

核心代码 ：

\u9898\u89e3 CF847B \u3010Preparing for Merge Sort\u3011

题意：

把一个数组分成若干个新的单调增的数组，每次选的元素若比新数组最后一个元素大则加入新数组。

\(n\leq 10^6\)。

对于每一次的组成新数组，新数组中后一个元素都是前一个元素之后第一个比它大的元素。

如果对于每一个新的数组只考虑最后的一个数的大小的话，最后会形成一个单调递减的序列，每次取出一个新的元素，若有数比他小，则可以与已有的新数组连接上。（笔者语言表述的不好，若难以理解可以直接看代码）。

如果有多个数组的尾数比该元素小，则接在其中尾数最大的一个数组后面。这个过程可以用二分查找来实现。

核心代码：

\u9898\u89e3 CF843C \u3010Upgrading Tree\u3011

题意：

每次可以对一个树经行最多 \(2n\) 次操作 \((x,y,y')\) 表示将 \((x,y)\) 删除，同时加入一条边 \((x,y')\) 。

每次操作要求 ：

每次操作中 \((x,y)\) 存在。

操作后仍然是树。

每次删了 \((x,y)\) 时，必须保证包含 \(x\) 的子树中的节点数比包含 \(y\) 的节点数大。

最后使得所有点距离的平方和最小。输出一种操作的方案。 \(n\leq 2\times 10^5\)。

直接莽：对于一次操作 贡献是： (能想到这种操作的也只有笔者这样的菜逼了)

\[\sum_{u\in V_x}\sum_{v\in V_y} \big( dis\left(u,x\right)+dis\left(y',v\right)\big)^2 -\sum_{u\in V_x}\sum_{v\in V_y} \big( dis\left(u,x\right)+dis\left(y,v\right))\big)^2 \]

\[=V_x \sum_{v\in V_y} \big(dis(y',v)^2-dis(y,v)^2\big)+ \sum_{u \in V_x} \sum_{v\in V_y}{2\times dis(u,x)\times(dis(y',v)-dis(y,v))} \]

\[=…=\text{不会} \]

考虑操作的特殊性，也就是第三点，对于子树节点的限制可以推出在每一次操作之后树的重心都不会变（根据重心的定义可知，两个重心也不会影响这个结论）。

考虑操作的局限性：无法增加和减少与重心的度数（如果是两个重心，那么这俩个重心的连这的边不会改变，其实两个重心的情况可以把这两个重心缩成一个）。

我们可以根据给我们的 \(2n\) 次操作，首先用最多 \(n\) 次的操作来把重心连出去的子树变成一条条链。

然后再用最多 \(n\) 次把重心连出去的子树变成菊花图（感性思考一下，菊花图的时候显然答案更优）。

部分代码：

\u9898\u89e3 CF843A \u3010Sorting by Subsequences\u3011

其实并不需要 Graphcity 巨佬题解里说的用 \(\rm Tarjan\) 找环。

题意：

将一个序列分成最多的子序列，使这些子序列按升序排序后，总体序列也成为一个升序序列。

\(n\leq 10^5\) 。保证序列中元素各不相同。

没思路的话直接看样例 \(1\) ，将序列整个排序后，把原来位置上的数与排完序的该数的位置连线结果是这样的。

（显然，目标的升序序列唯一）。

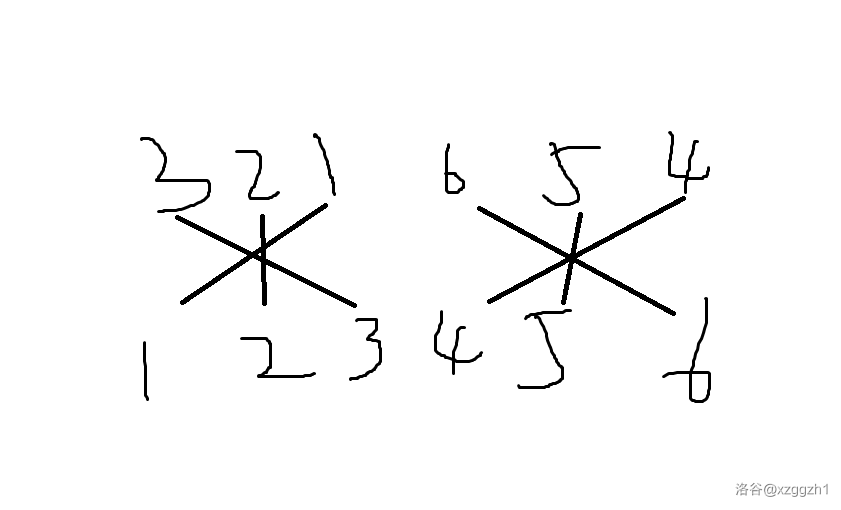
由于分出来的子序列必然是交际为空，并集为全集，所以若两个位置有连线，那么这两个位置必然在同一个集合里。

那么我们先排序，然后把对应位置的元素加入同一个集合中，最后输出有多少个集合和集合中的元素即可。这个可以用并查集实现，也可以直接模拟。

核心代码：

\u9898\u89e3 CF835E \u4ea4\u4e92 \u4e8c\u8fdb\u5236 \u5f02\u6216

我来讲讲怎么想出这题而不只是怎么解出这题。

题意：

有一个序列，其中有恰好 \(2\) 个数是 \(y\) ，剩下的 \(n-2\) 个数是 \(x\) 。

你每次可以询问一个集合的异或和。

你需要用不超过 \(19\) 次询问找到两个为 \(y\) 的数的下标。其中 \(n\leq 1000\) 。

要素察觉： \(\log\) 、异或、交互、找 \(2\) 个。

看到这里就应该可以想到这个著名的定理（误。

两个不同的数的二进制不完全相同。

这个套路有些常见，解法就是对于每个二进制询问这位上是 \(1\) 的位置的集合，那么必然有一次问到的集合中只包含其中一个。

上面是看到题后直觉的内容，下面讲思考的内容。

可以发现询问操作的具体作用：可以问得一个区间里面有偶数个 \(y\) 还是 奇数个 \(y\) （实现也非常简单，假设偶数个 \(y\) 然后看输入是否和假设之后的值一样即可）。

套路化的，先查询一遍每个二进制为 \(1\) 的位置的集合（消耗次数 \(10\) ）， 然后可以得出以下内容。

\(y1\) 和 $y2 $ 在每个位置上是否相同。（设 \(y1,y2\) 为这两个 \(y\) 的位置）。

我们只要问出 \(y1\), \(y2\) 中的一个即可得到全部答案。

这就要用到刚才那个著名的定理了，先随便取一个位 \(base\)，在这个位上， \(y1\) 和 \(y2\) 不相同。那么如果询问的集合中的 $base $ 位都是同一个值，那么这个集合中至多有 \(1\) 个 \(y\) 。

根据这个，那么就好处理了。先钦定 \(y1\) 的 \(base\) 位是 \(1\) （这样可以减少一次询问）。对于每一位 \(x(x\not = base)\) ， 都查询 \(x\) 和 $base $ 位都是 \(1\) 的位置的集合,可以得出 \(y1\) 在这个位置上是否是 \(1\) 就可以完整求出其中一个了，题目得解。

下面是核心代码：

\u9898\u89e3 CF835D \u3010Palindromic characteristics\u3011

和已有的一篇回文自动机的解法不同，这里给出的是简单的 $n\leq 5000 $ 的解法，做法是 dp。

题意：

给你一个串，让你求出 \(k\) 阶回文子串有多少个。其中：

题目中 \(n\leq 5000\)，直接考虑二维 \(dp\) 。

设 \(dp[i][j]\) 表示 \(s[i...j]\) 的回文阶数，若为 \(0\) 则不是回文串。

考虑从 \(dp[i+1][j-1]\) 到 \(dp[i][j]\) 的转移：

若 $s[i] \not = s[j] $ 或者 \(dp[i+1][j-1]=0\) 那么 \(dp[i][j]=0\) 。

否则 \(dp[i][j]=dp[i][i+(i-j+1)/2-1]+1\) 。（等于左半部分的阶数 \(+1\) ）。

知道转移，最后记得搞个前缀和就好了，这里是核心代码。

\u9898\u89e3 CF1452G \u3010Game On Tree\u3011

@duyi 巨佬的做法好麻烦啊，这里给出一个更容易的做法，代码难度，算法难度，和算法时间复杂度更加优秀。

题意：

\(a\) 被 \(b\) 的好多点在树上追（每回合 \(a\) 先动，然后 \(b\) 的所有点都单独动）， \(b\) 的点固定，问每一个 \(a\) 的位置， \(a\) 最多能保持多久不被追。

\(n\leq 10^{5}\)。

先考虑 \(a\) 的逃跑路径，其中设 \(dist[u]\) 表示 $u $ 到最近的 \(b\) 的距离， \(dis(a,b)\) 表示 \(a,b\) 的距离。

考虑 \(u\) 要到 \(v\) 只有当 $dist[v]>dist[u] $ 时，最后的答案是 \(dist[v]\)（跑到 \(v\) 然后等死），前提是 \(u \to v\) 时不被 \(b\) 抓 。

反着思考，即 $u $ 可以让所有 \((dis(u,v)<dist[u])\) 的 \(v\) 使 \(ans[v]=\max(ans[v],dist[u])\)，若只是朴素的用 \(\rm bfs\) 来更新，时间肯定不够，所以我们考虑剪枝。

我们按 \(dist[u]\) 降序排列，易知我们更新的时候不用取 \(max\) 而是直接覆盖没被覆盖过的即可，为了避免额外的遍历，我们只需开一个数组 \(now[u]\) 纪录当前遍历到 \(u\) 的时候 \(u\) 又去更新了与 \(u\) 相距多少的节点。

注：这里这个 \(now\) 比较难懂，下面放一个例子。

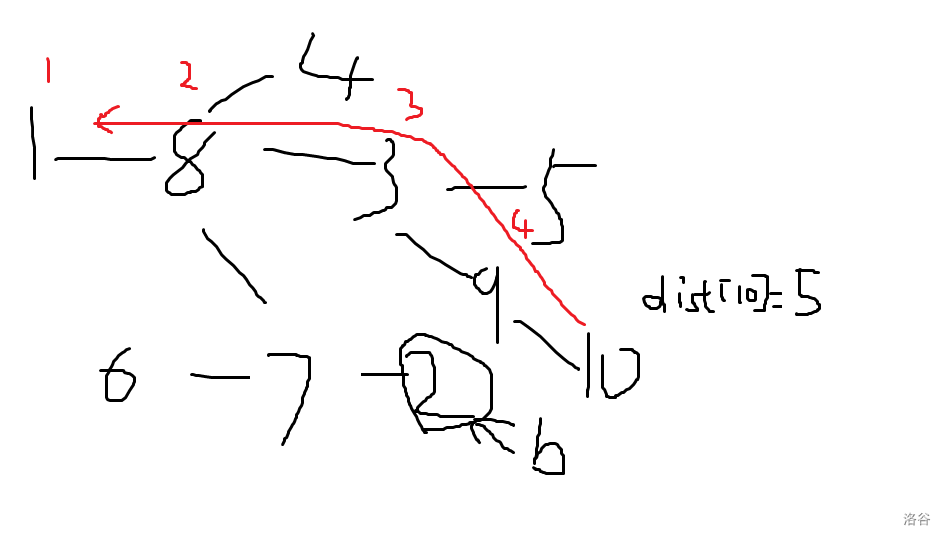
当我们以 $10 $ 为 \(u\) 来更新其他 \(v\) 的 \(ans[v]\) 时，这里的 \(now[1]=1,now[8]=2,now[3]=3,now[10]=5……\)

当我们 $\rm bfs $ 到一个点时，若此时的 \(u\) 给予下一个点的更新距离小于 原有的更新过的距离，那么就可以剪掉这个枝。

这部分的代码：

复杂度总体来说是 \(O(n\log n)\) 的，至少排序带一个 $\log $，后面部分也是 带 $\log $的。

但后面部分复杂度证明我不太会，但是可以感性理解，比如说第一次 \(u\) 离最近的 \(b\) 那部分的 \(now[v]\) 是不会被更新的，而 \(u\) 并非随便取的，而是取相对所有 \(b\) 最远。大概最终效果和启发式合并或者点分治差不多，真要严谨证明可以去看官方题解。

\u9898\u89e3 CF825F \u3010String Compression\u3011

题意：

给定一个串 \(s\) ，其中重复出现的子串可以压缩成 “数字+重复的子串” 的形式，数字算长度。

只重复一次的串也要压。求压缩后的最小长度。

\(|s|\leq 8000\) 。

字符串的题目还是不太熟练，这里给出一个 \(\rm KMP\) 优化的 \(\rm DP\) 算法。

但这题的解法不止于此，甚至这个方法可能算是小众解法。貌似 \(\rm hashing\) 和 \(\rm string \ suffix\ structures\) 或者 乱搞 都可以搞出来。

容易想到用 \(dp[i]\) 表示压缩到 \(i\) 时的答案，易知这是没有后效性的。

且 \(dp[i]\) 一定是要在所有的 \(dp[j] \ (1\leq j < i)\) 转移，因为仔细思考后发现不存在任何贪心策略可以优化转移，如 \(\rm aaaaabbabb\) 前面的连续的最后一个 \(\rm a\) 应该是放在后面跟优。

我们得到了一个大致的 \(\rm DP\) 的模型，那么具体如何优化转移？

为找到重复的串，我们可以利用 \(\rm KMP\) 算法的 \(\rm next\) 数组。

由于 \(\rm next\) 的意义是后缀可以匹配的最长前缀，很显然 \([\rm next[i],i]\) 是以 \(i\) 为结尾的循环串。

我们对于每一个点都跑一边从这个点开始的 $\rm KMP $ ，然后把这个点向后转移即可。

代码:（其中 \(cnt[i]\) 数组表示的是 \(i\) 的位数）

\u9898\u89e3 CF825D \u3010Suitable Replacement\u3011

咕咕咕

题目大意:

给出字符串s和t,字符串s中的'?'可以用字符串t中的字符代替,要求使得最后得到的字符串s(可以将s中的字符位置两两交换任意位置任意次数)中含有的子串t最多。

\u9898\u89e3 CF825C \u3010Multi-judge Solving\u3011

题意：

现在有 \(N\) 个问题，已知之前已经最难做到了难度为 \(K\) 的题，现在我们如果想要做一个题，我们可以做 $a_i \leq 2\times K $ 的题，每次做完难题之后，更新 \(K\) 值。

我们现在可以在其他OJ上做题，来提升自己的实力，问做完这 \(N\) 个题最少需要在其他OJ做几个题。

每一次到其他OJ上做题可以使得 \(k\) 变成原来的两倍，因为我们要最小化到其他OJ上做题的数量，所以每次做题的时候要让 \(k\) 变得尽可能大。

所以只要按照难度排序，贪心的只有当遇到难度高的没法做到的就去其他OJ上做题。

代码：

\u9898\u89e3 CF820B \u3010Mister B and Angle in Polygon\u3011

题意：

有一个正 \(n\) 边形，问哪 \(3\) 个点形成的角度最接近 \(a\) 。

这里可以做一个正 \(n\) 边形的外接圆，然后根据同弧所对的角相等这一个初中数学的知识，可以知道：这个角的大小只和他所对的弧长有关。又由于是正 \(n\) 边形，所以最多只有 \(n\) 个不同大小的角。

然后枚举就好了。

\u9898\u89e3 CF813D \u3010Two Melodies\u3011

题意：

给一个长度为 \(n\) 的序列,求两个不相交的子集长度之和最大是多少，能放入同一子集的条件是首先顺序不能变，然后每一个相邻的要么相差 \(1\) 或者相差 \(7\) 的倍数。 $n < 5000 $ 。

当我看到CF818G时，我发现这题不止 \(\rm DP\) 一种解法。甚至 \(\rm DP\) 的解法只能算是暴力。

CF818G 算的是四个不相交的子序列，而这题只要求两个，若用费用流的做法，那么只要改一下关键边的流量即可（当然，这题数据范围稍大）。

大致思路：

把一个点拆成两个点来限制每个点最多用一遍。

把模 \(7\) 相同的最近的数连边表示相差 \(7\) 的倍数的点有边。

把相同权的点搞在一起，然后差一的数连最近的，表示差 \(1\) 的点有边。

其中取一个数获得的贡献可以用边权表示，取的限制可以用流量表示。

这样最后边数大概是 \(O(n)\) 级别的（上面的连边中的细节略去，若细节不懂说明网络流的题刷的太少）。

最后跑费用流输出答案即可。

这个费用流写的好速度升值可以吊打 \(\rm DP\) 。并且更加普适，求多少个序列改变只需改变流量。

代码虽丑还是放一个吧：

\u9898\u89e3 CF818F \u3010Level Generation\u3011

题意：

对于 \(n\) 个点 $m $ 条边的简单无向图，如果有至少 $ \lceil\frac{m}{2}\rceil$ 条边是桥，则这个图是 “绝妙的” 。 \(q \ \ (q\le 10^5)\) 次询问，求出 \(x \ \ (x\le 2\times 10^9)\) 个点的 “绝妙的” 图中，最多有多少条边。

由于边双连通分量中不存在桥，然而我们又想让桥相对于所有边最多。所以我们可以直接贪心的考虑就在一条链上只搞一个边双联通分量。

设边双联通分量里面有 \(x\) 条边，那么答案将会是

\[\min ( \frac {x(x-1)} {2} +n-x, 2(n-x)) \]

最后输出所有 \(x\) 里面答案最大的，化简之后可知左边的东西单调增，右边的东西单调减，所以可以二分交点，算出最值。

注意：也许交点不是整数所以要在二分值附近多试一个点。

核心代码：(式子以化简)

\u9898\u89e3 CF811B \u3010Vladik and Complicated Book\u3011

题意：

有一个长度为 \(n\) 的排列，每次选一段区间 \([l,r]\) 排序，问位置 \(x\) 上的数在排序前后是否发生了改变。保证 \(x∈[l,r]\) 。

由于 \(n,m \leq 10^4\) 所以 \(O(n\times m)\) 的暴力可以过。

每次循问的时候遍历区间，查找在区间中比位置 \(x\) 的数小的数，然后计算排名是否与原来在区间里的位置相同即可。

当然，若数据范围增大也可以用主席树来搞。

代码：（主席树）

\u9898\u89e3 CF799C \u3010Fountains\u3011

题意：

\(n\) 个物品，每个都有价值和美观值，每种商品只能被金币和钻石其中之一购买。

你有 \(x\) 个金币和 \(y\) 个钻石，买两个物品做多可以有多少美观值。

题目拿到手直接分类讨论：把花金币的物品分为一类，把花钻石的物品分为一类，就有以下两种情况。

两个物品不属于同一类。

两个物品属于同一类。

情况 1 直接贪心取每类能买到的最大值即可，我们直接考虑情况 2 。

枚举先买那个物品，可以算出剩下货币的数量。然后找到剩下货币能买的物品里面美观最大的。

如何快速找：直接按照花费排序，然后建一个线段树维护区间最大美观度即可。

核心代码：（线段树部分略去）

\u9898\u89e3 CF793E \u3010Problem of offices\u3011

咕咕咕，等着没题解氵的时候写。

\u9898\u89e3 CF793D \u3010Presents in Bankopolis\u3011

题意：

一个有向图，节点有编号，找一条经过 \(k\) 个点的最短路径，要求是当前边不能跃过已经经过的节点。即对于路径中的边 \(x \to y\) ，不存在以前经过的点 \(t\) 使得 \(x &lt;t&lt;y\) 。

$ 1 \leq n,k \leq 80 $ ， $ m \leq 2000$ 。

每一次经过一条边都会使得可以到达的边的范围缩小。

考虑到 $ 1 \leq n,k \leq 80 $ 我们不难想到直接把可以去的区间存下来做 \(\rm DP\)，

再按照类似区间 \(\rm DP\)的做法开一维 \(0,1\) 表示当前到达的端点是左端点还是右端点，然后直接转移即可。

具体的说，我们可以设 \(f[i][j][k][0/1]\) 表示经过 \(i\) 个点，可以去的区间是 \([j,k]\) ，现在在 左端点/右端点。其中第一维可以用滚动数组存。

剩下的一些小细节可以看代码：

\u9898\u89e3 CF793C \u3010Mice problem\u3011

题意：

给你一个捕鼠器坐标（为矩形），和各个老鼠的的坐标以及相应坐标的移动速度，问你是否存在一个时间点可以关闭捕鼠器抓住所有的老鼠，相对误差不能超过 \(10^{-6}\)。

是一道比较普通的计算几何的题。

我们只要把每一个老鼠在矩形里的时间段算出来然后取交集，若交集非空则输出交集中的任意点即可。

主要有以下两个要点：

计算每一只老鼠在矩形里的时间：将横坐标和纵坐标分开计算取交集即可。

如何取交集：交集的左端点是所有集合的左端点的最大值，交集的右端点是所有集合右端点的最小值。

（由于集合都是连续的，所以这个方法的正确性反证即易证）。

核心代码：

\u9898\u89e3 CF788A \u3010Functions again\u3011

不是很理解为啥有的题解都是动态规划做的，还有一个带 \(\log\) 的……

题意：

给定 \(n\) 个数，求

\[\large f[l,r]=\sum^{r-1}_{i=l} | \ a[i]-a[i-1] \ | \times (-1)^{i-l} \]

的最大值。

首先，这个 \(f\) 的值和原来的 \(a\) 并没有关系，我们只需考虑其差分数组的绝对值即可。

当你把这个转换过了的数组搞出来， 就会发现对于取的区间就是所有奇数位取正，然后偶数位取负的和，对于每个起始位奇偶性相同的区间，他们其实用的都是同一个数组。

然后你会发现，其实题目就转换为求分别两个数组的最大子序列和，其中一个数组原差分数组的绝对值在奇数位取负，一个是在偶数位取负。

最大子序列和就只要贪心就好了。

具体实现也简单，可以看代码。

\u9898\u89e3 CF780E \u3010Underground Lab\u3011

题意：

给出一个图，有 \(n\) 个点, \(m\) 条边， \(k\) 个人，每个人至多只能走 \(\lceil \frac{2n}{k} \rceil\) 步,要求每个点都被走到过，输出可行的方案即输出每个人所走的步数和所走点。

题解：

看到 \(\lceil \frac{2n}{k} \rceil\) 可以想到答案也许和 \(2n\) 有关。

其实这里的 \(k\) 个人和 \(1\) 个人是没有区别的，我们只要先考虑一个人怎么走过这 \(n\) 个点。

只要 dfs 一下，纪录一下 dfs 时候的顺序即可，注意回溯的也要加入。

这样每个点最多会被到达两次（第一次到达和回溯到这个点）。

最后把这个 dfs 出来的序列分成 \(k\) 段输出就好了。

核心代码（这里考虑直接搞成树，就不用多余的边）：

\u9898\u89e3 CF773A \u3010Success Rate\u3011

怎么题解里都是二分，这个可以不用二分而是直接 \(O(1)\) 输出。

题意：

一共 \(t\) 组数据,每组数据给出 \(4\) 个整数 \(x,y,p,q\) 。现在你一共提交了 \(y\) 次，AC的次数是 \(x\) 次。问你至少要再提交多少次，能让正确率刚好为 \(\frac p{q}\)。如果不可能，输出一行 \(-1\) 。保证 \(y&gt;0,q&gt;0\) ， \(p\) 和 \(q\) 互质。

直接考虑AC率是比较麻烦的，因为多了一次AC则多了一次提交，所以并不好直接算。

显然这个问题直接贪心就好了，考虑AC个数能使WA是整数的AC最少次数，然后计算即可。

对于无解的情况，只有全AC或全WA然后现有状况与输入不符合才会无解（原因留给读者自行思考）。

核心代码：

\u9898\u89e3 CF763E \u3010Timofey and our friends animals\u3011

题意:

给你 \(n\) 个点，已知 \(m\) 对关系 \([u,v] \ (|u - v| \leq k)\) 给出，询问 \(q\) 次，每次问你 \([l,r]\) 有多少个连通块。

有多少联通块？这不是只要把环去掉，然后算一算 \([l,r]\) 里面的边数就好了？（显然按照长度排序，最长的边若构成环则直接忽略，然后区间中多一个边就少一个联通块）

至于怎么算，直接暴力前缀和维护端点，然后 \(O(k^2)\) 枚举哪些边是一个端点在区间里的减掉贡献就好了（其中 \(k \leq 5\)）。要啥回滚莫队，要啥线段树？

这个维护的办法多得很，我的具体做法是开两个前缀和数组纪录左端点和右端点，然后区间 \([l,r]\) 里边的个数就是

\[Cnt1_{r}-Cnt2_{l-1}+Del \]

表示到 \(r\) 所有边右端点的和 减去 到 \(l\) 所有左端点的和 加上左端点在 \([l,r]\) 但右端点大于 \(r\) 的边的数量。

代码：

\u9898\u89e3 CF730B \u3010Minimum and Maximum\u3011

是一道挺好的交互题。

我们可以利用分而治之的思想来解决这个问题，毕竟这个上限决定了算法的大致复杂度。

考虑将这么多数字分为两组，先两两比较，把大的分为一组，小的分为一组，最大值只会在大的一组里，最小值只会在小的一组里（显然）。

那么现在是不是只用了 $ \frac n 2$ 次就把问题的规模转换成了 \(\frac n2\)。

所以一直这么操作直到一组只剩下一个数字，复杂度正确。

核心代码：

\u9898\u89e3 CF729E \u3010Subordinates\u3011

题意：

一个公司有n个员工，除了主管之外，每个员工都有一个直接上级。要求每个工人告诉他们有多少上级。有些工人很匆忙，犯了个错误。你要找出可能犯错误的最少工人人数。

我们考虑对于一个合法的序列它应该是怎么样的。

除了根节点，每一个点都有一个父亲，很显然，这个点的祖先个数一定比它父亲节点多一。

那么如同 \(0,1,1,2,2,3,4\) 或 \(0,1,2,2,2,2,3\) 等都是合法的序列。

即 \(0\) 有且只有一个，其他的数都是连续的（在升序排列后）。

想到这里，这个题就很简单了，只要贪心的把大的数填到小的“缺口”里就好了。

核心代码：

\u9898\u89e3 CF727D \u3010T-shirts Distribution\u3011

题意：

有 \(6\) 种尺码的衣服，有的人只适合 \(1\) 种衣服，有的人适合相邻的 \(2\) 种,问是否存在合法方案，并输出。

首先，如果一些人只适合一种衣服，那么根本不有抉择，直接减去即可。

然后我们考虑剩下的人。

每一个人都有两种选择，这是网络流的经典题，但这里并不用，直接贪心即可：

对于只适合第一种和第二种的，优先选择第一种，然后考虑只适合第二种和第三种的……显然，每次我们考虑的时候优先选的那一种在当时的情况下只能为一种人做出贡献，不然就直接浪费了，所以贪心的先选就好了。

核心代码:

\u9898\u89e3 CF721D \u3010Maxim and Array\u3011

题意 ：

最小时的每个元素。

这道题要用到经典的贪心策略：

若要使得，

\[\prod_{i=1}^n \lvert a_i\rvert \]

变到最大，每次需要取出来，

\[u =\min_{i=1}^n |a_i| \]

将 \(u\) 变成 \(u+x\) 。

反之，若要使那个式子减到最小（其中 $x \leq |a_i| $），也是取出绝对值最小的 \(u\) 变成 \(u-x\) 。

这样这个题就很好做了，求连乘的最小值，先搞到结果为负。

然后开一个优先队列每次取一个绝对值最小的数把他绝对值搞大就好了。

核心代码：

\u9898\u89e3 CF717H \u3010Pokermon League challenge\u3011

大概题意：

有 \(n\) 个教练，和 \(t\) 个现有的教练团队，每个团队都属于两个协会中的一个。有e对训练师互相憎恨。他们的仇恨没有重边和自环。每个教练都有一个愿望清单，列出他想加入的团队。你的任务是将球员分成小组，并将小组分成两个会议，以便：

每个教练都属于一个团队；

没有团队参加两个协会；

协会之间的总仇恨至少为 $ \frac{e}2 $；

每一位教练都是从他的愿望清单中选出的一个团队。

会议之间的总仇恨计算为来自不同会议的团队中互相憎恨的培训师对的数量。

是一道非常神奇的题目。cf里这个题有probabilities的标签。

拿到题目，简单思考：总仇恨值至少为 $ \frac{e}2 $，这个值是不是有一点点低？

稍加思索：简化模型，若我们随机选团队，团队随机选协会，那么可以看做每个教练都随机分布在两个协会中且概率相等（这里是简化了的模型，大致可以这么认为）。

那么考虑每一条憎恨的边，易得其有一半的概率对总仇恨产生贡献，那么所有边的总贡献的和的期望值就是 $ \frac{e}2 $ 。

并且可以认为每一条边的产生贡献和不产生贡献其实是等价的，也就是纯随机总贡献有一半以上的可能是符合条件的。这样我们随便随机几次就可以随机出答案： 设随机了 \(k\) 次，那么所有的随机都没有成功的概率就是 \(\frac1{2^k}\) ，期望两次就可以随机出答案，随机 \(20\) 次几乎不可能失败。

核心代码：

\u9898\u89e3 CF717C \u3010Potions Homework\u3011

题意：

每个人有一个懒惰值，每个任务有个难度，一开始每个人的任务的难度和懒惰值都为 \(a_i\)，完成任务时间是懒惰值乘以难度，现在重新分配任务，问花费的时间最小是多少。结果模 \(10007\) 。

就是让懒的人完成简单点任务。

证明如下：

对于两个人的懒惰程度和对应任务的难度 \(x_1,x_2,y_1,y_2\) ，令

\[x_1 \leq x_2,y_1 \leq y_2 \]

有：

\[x_1 * y_1+x_2*y_2 \leq x_1*y_2+x_2*y_1 \]

移项相消即可看出。

记得开long long。

代码：

\u9898\u89e3 CF713B \u3010Searching Rectangles\u3011

题意：

可以先二分答案出两个矩形的分界线，然后对于每一个矩形二分他的位置。

显然每个完整的二分只要log(n)次，总共的 \(200\) 次绰绰有余。

代码：

\u9898\u89e3 CF707B \u3010Bakery\u3011

题意：

有N个城市，M条无向边，其中有K个城市是仓库。

现在要在非仓库的城市中选择一家开面包店，使得其最少与一个仓库联通，且到所有仓库距离的最小值最小。

考察你最基本的图论建图能力。

就是对于每一个仓库考虑与它有连边的非仓库的最短距离。

（为什么这么做是对的，因为除了仓库，所有点都是非仓库，那么如果最后选的点和最靠近它的仓库不是相邻的，那么必然可以在这个点与最靠近它的仓库的路径上选一个点使得答案可以更小）

然后把所有的取一个最小值，若所有仓库旁边都没有非仓库，那么输出 $ -1$ 。

代码：

\u9898\u89e3 CF690C3 \u3010Brain Network (hard)\u3011

题意：

这个问题就是给出一个不断加边的树，保证每一次加边之后都只有一个连通块（每一次连的点都是之前出现过的），问每一次加边之后树的直径。

考虑先离线，这样方便LCA预处理出所有点之间的距离。

然后每次加入一个点，我们可以轻易证明一个结论：

每次加入点后，一定能够找到一条新的直径和加入这个点之前的一条直径存在公共点。

所以我们记录每一个状态下的直径的端点 \(u,v\) ，然后每一次加点判断这个点和 \(u,v\) 的路径长度是否比原来的直径长，若长则更新直径。

核心代码：

\u9898\u89e3 CF689C \u3010Mike and Chocolate Thieves\u3011

题意：

有四个数组成一个等比数列.

给你一个 \(n\) ，找一个最小数 \(t\) ，使得在 \(t\) 内有 \(n\) 组等比数列成立。

假设这四个数为 \(a_1,a_2,a_3,a_4\) 他们的公比为 \(q\) 。

显然有 \(a_1*q^3 = a_4\) ， \(a_1\) 可以任意取，所以对于一个 \(t\)，

有 $\lfloor \frac t {d^3} \rfloor $ 组公比为 \(d\) 的组合。

若想求出所有小于 \(t\) 的组合，那么只要枚举 \(d\) 即可，单个时间复杂度是 \(O(t^{\frac13})\) 。

现在我们已经可以容易地计算所有小于 \(t\) 的组合，所以只要二分这个 \(t\) 就可以解决了。

代码:

\u9898\u89e3 CF686B \u3010Little Robber Girl\u0027s Zoo\u3011

题意：

将一个 \(n\) \((1 \leq n \leq 100)\)个元素的序列排成非递减序列，每次操作可以指定区间 \([ L，R ]\)（区间内元素个数为偶数），将区间内第一项与第二项交换，第三项与第四项交换，第五项与第六项……在 \(20000\) 次内完成排序，输出每次操作。

我们只考虑每次操作一个长度为 \(2\) 的区间，就是交换相邻项，让序列变得有序。

你想到了啥？ 对，冒泡排序。

众所周知，冒泡排序的交换次数在 \(O(n^2)\) 左右，当然这个 \(n^2\) 在绝大多数情况下是超过实际比较次数的。

所以可以在 \(20000\) 操作内完成 $ 100 $ 个数的排序。

代码:

\u9898\u89e3 CF685E \u3010Travelling Through the Snow Queen\u0027s Kingdom\u3011

题意：

给你一张图，每一条边都有一个编号 \(i\) ，经过每条边的时间为 \(1\) ，如果当你到达这条边的时间小于 \(i\) 的话，就必须等到i才能走出这条边，如果大于 \(i\) ，就走不出去了，也就是不通了。然后给你一些询问 \(l\) , \(r\) , \(s\) , \(t\) ，问你是否可以从 \(s\) 出发，时间为 \(l\)，在 \(r\) 时间之前到达 \(t\) 。

注意到 \(n \leq 1000 \ , m\leq 200000\) ，我们直接考虑 \(O(n*m)\) 的算法。

首先考虑只有一个询问，那么直接把编号大于某个值的边取出再类似地跑一边“最短路”，看最后的时间是否小于 \(r\)。

但是现在有许多询问，对于每一个询问重新建图显然时间上无法满足题目的要求，那么我们可以容易得想到：离线处理每一个询问，将询问的 \(l\) 按照降序排列，同时每一次取出编号最大的边加入，并更新“距离”（最小所需时间），这样就可以轻易处理出所有询问。

至于如何加入边并同时维护距离，我们先记录每两个点之间的“距离”，每次加边并对每个点到这条边的端点进行松弛操作。

这样总的时间复杂度为 \(O(n*m)\) 。

代码:

\u9898\u89e3 CF682E \u3010Alyona and Triangles\u3011

这个题除了 @辰星凌 的做法，还有更加简单的做法。

首先，稍微有点几何基础的人都知道，只要找到最大的三角形，再让这个三角形向三遍各扩展一倍，就找不到不被大三角形包含的点。

然后就是如何找到最大的三角形。

其实有一种比较简洁的方法：先任意取三个点，然后每次遍历所有点，如果这个点把三个点之中的一个点换掉可以使得三角形扩大，那就保留换的操作。

注意到 \(n\leq5000\) ,在对算法略加分析，发现时间其实很充裕。跑得最慢的点不到50ms。

下面是核心代码:

\u9898\u89e3 CF681E \u3010Runaway to a Shadow\u3011

一道比较容易的计算几何题。

题意:

一个蟑螂等概率随机向任意方向跑最多 \(t\) 秒。

问最后停在 \(n\) 个圆中的概率。

转化一下题意，等价于

求一个圆和其他所有圆的交集所对的角度的并集。（表述可能略有偏差）

对于每一个圆都分类讨论和一开始圆的交集所对的角度。

然后把这些角度放到一个容器里合并然后算出概率。

需要注意精度的优化。

\u9898\u89e3 CF681D \u3010Gifts by the List\u3011

我感觉现有的那一篇题解的做法复杂了。

题意:

一个家族有 \(n\) 个人， \(m\) 种关系，每一种关系表示 \(x\) 是 \(y\) 的祖先，祖先具有传递性，然后有 \(n\) 个数，表示第 \(i\) 个人想把礼物送给 \(a[i]\) , 你需要构造一张表这张表上的人代表收礼物的人，并且其他人送礼物是按表上的顺序找，找到的第一个祖先就是他要送礼的人，同时需要满足这个人是他想送礼的人，如果存在这张表输出人数及编号，否则输出 \(-1\) （题意中自己也算是自己的一个祖先）。

题解：

稍微读一读题目，反复理解一下题意，就会发现其实这个题目这么长其实说的就是一件事情：

对于甲的祖先里和甲不是同一个目标的人乙必有甲的目标不是乙的祖先。

用反证法证明：

若甲的目标是乙的祖先，那么要是甲送给他的目标礼物，乙也必须送给这个人礼物而不是他原来的目标。

如何用程序来解决这个事情。

建图时先将所有祖先向他儿子建里单向变，然后从零入度的点开始遍历。

使得对于所有点都有 他的目标为他自己 或 他的父亲和他是同一个目标，那么就可以构造出一个合理的方案。

到这里，题目已经可以解决了，但是其实上面那个条件我这里只证明了他是有合理方案的必要条件，而这个条件的充分性可以留给读者自己思考，这里不多赘述。

下面是代码：

\u9898\u89e3 CF681C \u3010Heap Operations\u3011

没看到 c++ 的题解，就来写一篇好了。

题意：

给你部分小根堆的操作，让你补全所有操作。

操作包含三种：

1.插入元素。

2.删除一个最小元素。

3.查询最小元素。

首先，c++的STL中已经内置了优先队列的容器，所以可以直接拿来用。

以下是实现小根堆基本操作。

然后考虑原题，思路是模拟。

稍加思考可以轻易知道：无论堆中状态如何，都可以实现第三个操作（最纯的方法就是弹出所有数，再加入一个数）。

所以我们对于前两个操作可以不用修改，直接加入或删除。

但是每到第三个操作就把所有数弹出的策略显然不能通过，所以我们考虑优化：

若查询的元素是最小的元素，什么都不用做。

若查询的元素比堆内最小的元素还小，直接插入该元素即可。

若查询的元素大于堆内最小的元素，弹出堆顶元素直至堆为空或者堆内最小元素比该元素小，最后再插入该元素。

除了以上谈到的之外，本题还有一些细节需要注意。

具体可以看代码:

\u9898\u89e3 CF677E \u3010Vanya and Balloons\u3011

CF677E 【Vanya and Balloons】

题意：

有一个矩阵，矩阵里只有 \(0，1，2，3\) ,求一个乘积最大的十字形（可以横着摆，可以竖着摆放）。

看到那么多数的乘积，如果直接纪录因子 \(2\) 和 \(3\) 的个数，很难比较两个数的大小，因为 \(n\) 最大可以有 \(10^3\) ，直接算出答案显然不是正确做法。

那么考虑换一种方式比较每个乘积值的大小。

其实很多人看到连乘就会想到取对数，由对数的运算法则可以把许多数的乘积“打下来”，变成许多数的求和。显然地，对数函数在其定义域上单调递增。

所以我们可以用一个数的对数值来代替其原值以方便比较大小。

那么这个问题就可以简化了，把每个数取对，然后乘积变成和，找到最大和的取法，计算答案。

代码：