动态规划——入门
动态规划(入门)
在之前贪心算法的部分,有一部分问题使用贪心算法无法求得最优解,但是使用动态规划就可以求出最优解。
在现实生活中,有一类活动的过程,这个过程可以分为若干个有联系的过程,每一个阶段都需要作出决策,从而使得整个活动达到最好的效果。各个阶段的决策依赖于当前的状态同时又影响着以后的发展,而每个阶段的决策一般来说和时间有关,每一次决策会引起状态的变化,一个决策序列就是这样动态产生的,有动态的含义。
故动态规划实际上就是解决多阶段决策最优化的过程的方法。
举例来说,假定从\(A\)到\(D\)需要铺设管道,其中要经过两级中转站,连线上的数字表示距离,如下图所示,应该选择什么路线,使得总路线最短?
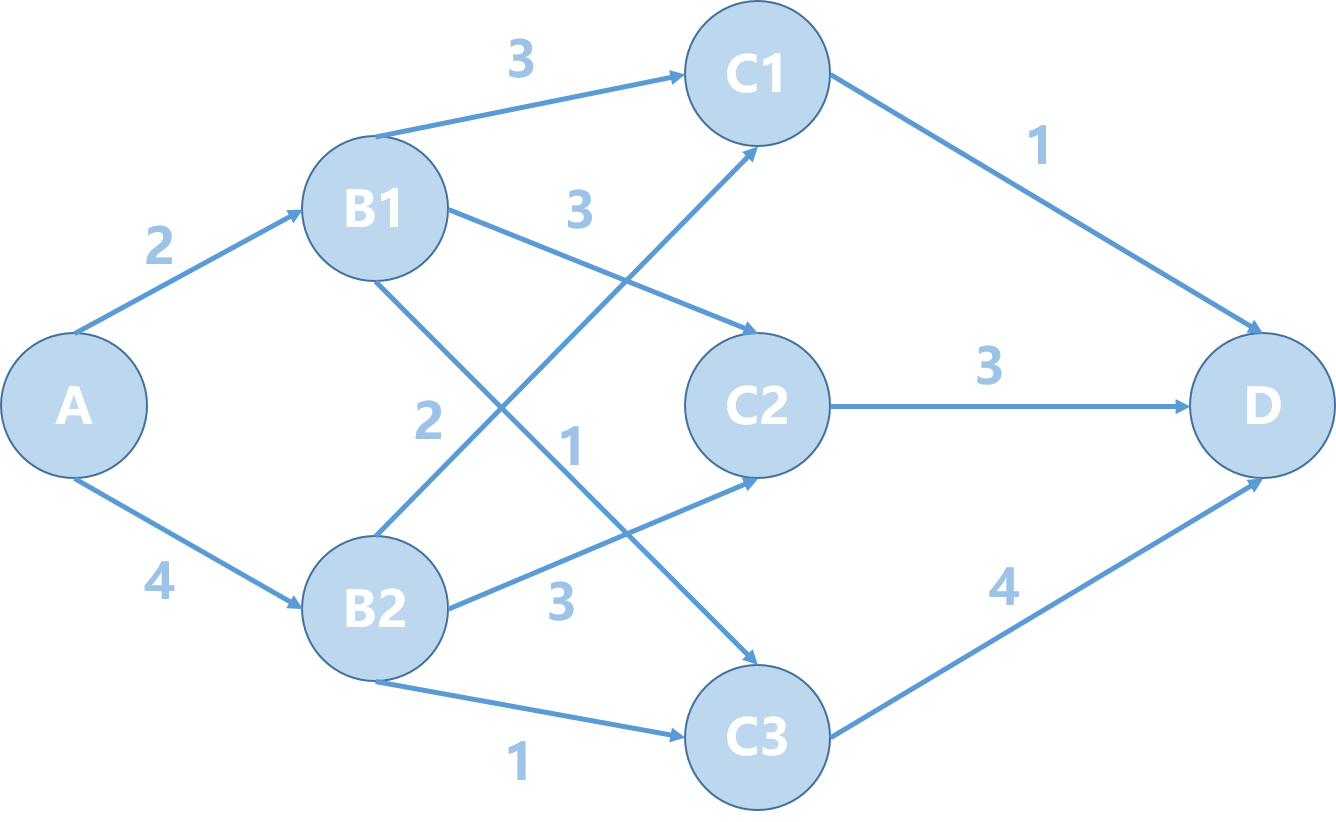
按照之前学过的贪心策略,从\(A\)出发,每次选择距离最短的路径,直到\(D\),得出的答案为\(A->B1->C3->D\),总距离为\(7\)。但是实际上的最短路径为\(A->B1->C1->D\),长度和为\(6\)。错误的原因在于贪心求解的问题是子问题相互独立,没有联系的,仅仅有先后顺序,合起来正好是原问题。而上面的最短路径的各个子问题都是有关联的,用贪心求解是错误的。需要使用动态规划。接下来从两个实例来说明动态规划的特点。
引例、数塔
给你一个数字三角形,要求找出从第一层到最后一层的路径,使得所经过的权值和最大。
三角形如下
7
3 8
8 1 0
2 7 4 4
4 5 2 6 5
我们首先将这个大的三角形拆分为最小单位,如下

显然,最大路径权值和为\(7(2+5)\),如果是三层呢?
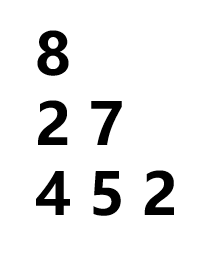
是否可以参考\(2\)层的做法,如果只考虑上面两层,那么最大的路径应该是\(8\)加上\(2\)和\(7\)中大的那个路径。
但是\(2\)和\(7\)分别都有子路径,刚才的分析,\(2\)的子路径中最优的为\(2+5=7\),而\(7\)的子路径中最优的为\(7+5 = 12\)。回归到这个\(3\)层的数塔中,如果中间那层已经是最优的路径了(包含其子路径)也就是\(7\)和\(12\),那么就和\(2\)层的问题相同了。
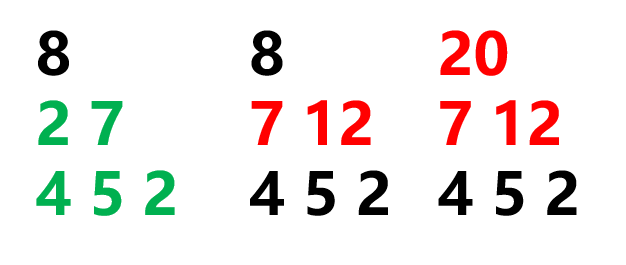
按照上面的方式推导,如果没有数塔中从下往上每一个数字都是到达当前数字的最优路径,那么往上推导时,只需要考虑\(2\)层数塔的问题即可。
其实刚才的分析过程中,通过子问题的最优解,推导出整个问题的最优解,并且每个子问题之间有联系。其实这就是最优子结构(问题的最优解包含子问题的最优解)。
具体实现可以通过数组\(d[i][j]\)表示第\(i\)层\(j\)列这个点到最后一行的最优解,显然根据上面的分析,我们的子问题是重叠的。可以有如下递推式
\(d[i] [j] = a[i, j] + max { d[i+1] [j], d[i+1] [j+1] }\)
每一层的取值,只和下一层有关,只需要考虑这一层是从\(d[i+1] [j]\)还是\(d[i+1] [j+1]\)走过来的即可,不需要关心\(d[i+1] [j+1]\)和\(d[i+1] [j]\)是怎么得到的。这就是无后效性。
程序设计可以从底部向上推导,也可以从上往下推导。或者采用记忆化搜索等方式。
参考程序
#include <iostream>
#include <algorithm>
#define N 1005
using namespace std;
int a[N][N];
int main () {
ios::sync_with_stdio(0);
int n;
cin >> n;
for (int i = 1; i <= n; i++)
for (int j = 1; j <= i; j++)
cin >> a[i][j];
for (int i = n - 1; i >= 1; i--)
for (int j = 1; j <= i; j++)
a[i][j] += max(a[i+1][j], a[i+1][j+1]);
cout << a[1][1];
return 0;
}
小结
动态规划的一些基本概念
- 阶段:根据时空顺序对问题求解划分阶段
- 状态:描述事物的性质,取决于你如何去思考这个问题的性质特点。对问题求解状态的描述是分阶段的
- 决策:是一种状态转移的选择,从当前状态转移到下一状态
- 状态转移方程:数学公式描述与状态有关的演变规律
动态规划的一个模型、三大特点
- 多阶段决策最优解模型
- 最优子结构
- 问题的最优解包含子问题的最优解。可以通过子问题的最优解推导出问题的最优解,也可以理解成后面阶段的状态可以通过前面的状态推导出来
- 无后效性
- 在推导后面阶段状态的时候,我们只关心前面阶段的状态值,不关心这个状态是怎么一步步推导出来的
- 某阶段状态一旦确定,就不受之后阶段的决策影响
- 重复子问题
- 不同的决策序列,到达某个相同的阶段时,可能会产生重复的状态。
例题
例1、导弹拦截
某国为了防御敌国的导弹袭击,发展出一种导弹拦截系统。但是这种导弹拦截系统有一个缺陷:虽然它的第一发炮弹能够到达任意的高度,但是以后每一发炮弹都不能高于前一发的高度。某天,雷达捕捉到敌国的导弹来袭。由于该系统还在试用阶段,所以只有一套系统,因此有可能不能拦截所有的导弹。
输入导弹依次飞来的高度(雷达给出的高度数据是\(≤50000\)的正整数),计算这套系统最多能拦截多少导弹。
【输入格式】
\(1\)行,若干个整数(个数\(≤100\))
【输出格式】
\(1\)行,表示这套系统最多能拦截多少导弹。
【输入样例】
389 207 155 300 299 170 158 65
【输出样例】
6
该问题的本质是寻找一个最长不下降子序列(该子序列可以不连续)。
那么划分阶段可以根据导弹来,第几个导弹就是第几个阶段
假定,要拦截当前飞来的导弹,那么需要找到此前飞来的导弹中,已经被拦截的数量最多的系统,来进行拦截,并且要保证当前的导弹高度不超过这个系统的最后一枚导弹高度。
可以定义\(d[i]\)表示从\(1\)到\(i\)枚导弹中,拦截\(a[i]\)导弹的系统最多能拦截的导弹数量,满足最优子结构。\(d[i]\)这个状态明显应该从\(1\)到\(i-1\)枚导弹中大于等于\(a[i]\)且\(d[j]\)的值最大的状态转移过来,满足无后效性。
参考程序
#include <iostream>
#include <algorithm>
#include <cstdio>
#define N 105
using namespace std;
int main () {
int a[N], d[N], ans = 0;
int n = 1;
while (scanf ("%d", &a[n]) != EOF) {
d[n] = 1;
n ++;
}
n --;
for (int i = 1; i <= n; i++) {
for (int j = 1; j < i; j++) {
if (a[i] <= a[j] && d[j] + 1 > d[i]) {
d[i] = d[j] + 1;
if (d[i] > ans)
ans = d[i];
}
}
}
printf ("%d", ans);
return 0;
}
例2、挖地雷
在一个地图上有\(N\)个地窖\((N≤20)\),每个地窖中埋有一定数量的地雷。同时,给出地窖之间的连接路径。当地窖及其连接的数据给出之后,某人可以从任一处开始挖地雷,然后可以沿着指出的连接往下挖(仅能选择一条路径),当无连接时挖地雷工作结束。设计一个挖地雷的方案,使某人能挖到最多的地雷。
【输入格式】
有若干行。
第\(1\)行只有一个数字,表示地窖的个数\(N\)。
第\(2\)行有\(N\)个数,分别表示每个地窖中的地雷个数。
第\(3\)行至第\(N+1\)行表示地窖之间的连接情况:
第\(3\)行有\(n-1\)个数(\(0\)或\(1\)),表示第一个地窖至第\(2\)个、第\(3\)个、…、第\(n\)个地窖有否路径连接。如第\(3\)行为\(11000…0\),则表示第\(1\)个地窖至第\(2\)个地窖有路径,至第\(3\)个地窖有路径,至第\(4\)个地窖、第\(5\)个、…、第\(n\)个地窖没有路径。
第\(4\)行有\(n-2\)个数,表示第二个地窖至第\(3\)个、第\(4\)个、…、第\(n\)个地窖有否路径连接。
… …
第\(n+1\)行有\(1\)个数,表示第\(n-1\)个地窖至第\(n\)个地窖有否路径连接。(为\(0\)表示没有路径,为\(1\)表示有路径)。
【输出格式】
有两行
第一行表示挖得最多地雷时的挖地雷的顺序,各地窖序号间以一个空格分隔,不得有多余的空格。
第二行只有一个数,表示能挖到的最多地雷数。
【输入样例】
5
10 8 4 7 6
1 1 1 0
0 0 0
1 1
1
【输出样例】
1 3 4 5
27
注意路径是单向路径。
用\(f[i]\)表示到挖到\(f[i]\)这个地窖,能够挖到的最多地雷数量。答案就在f序列中最大的那个值上。
状态转移方程如下:
\(f[i] = f[j] + a[i] {1<=j <i \,\,\, and \,\,\, f[j]+a[i] > f[i]}\)
翻译过来就是找到能够通往当前地窖中的地窖,并且地雷数量最多的地窖,将地雷数转移过来。前提是之前的地窖也都满足这个最优子结构。
参考程序
#include <iostream>
#include <cstring>
#define N 25
using namespace std;
int a[N], f[N], p[N], g[N][N];
void put_seq (int x) {
if (x == p[x]) {
cout << x << " ";
return;
}
put_seq(p[x]);
cout << x << " ";
}
int main () {
memset(p, -1, sizeof(p));
int n, mx = 1;
cin >> n;
for (int i = 1; i <= n; i++) {
cin >> a[i];
f[i] = a[i];
if (f[i] > f[mx])
mx = i;
}
for (int i = 1; i < n; i++)
for (int j = i+1; j <= n; j++)
cin >> g[i][j];
for (int i = 1; i <= n; i++) p[i] = i;
for (int i = 2; i <= n; i++) {
for (int j = 1; j < i; j ++) {
if (g[j][i] && f[j]+a[i] > f[i]) {
f[i] = f[j] + a[i];
p[i] = j;
if (f[i] > f[mx])
mx = i;
}
}
}
put_seq(mx);
cout << "\n" << f[mx];
return 0;
}
总结
动态规划的核心思想就是记录结果再利用,从而避免子问题重复计算,采用空间换取时间效率。
一般来说,解决动态规划问题有\(4\)个步骤
- 刻画一个最优解的结构特征。
- 找出状态转移方程。
- 计算最优解的值,通常采用自底向上的方法。
- 利用计算出的信息构造一个最优解。
动态规划类的问题包含两个重要要素
- 最优子结构
- 重叠的子问题


 浙公网安备 33010602011771号
浙公网安备 33010602011771号