对递归的理解

  二叉树中的遍历以及线索二叉树的创建对递归的使用非常频繁，递归对我来说也一直是模糊不清的概念。

  故写下此篇文章帮助理解递归。

一.递归的定义

  "一个函数在它的函数体内调用它自身称为递归调用，这种函数称为递归函数。执行递归函数将反复调用其自身，每调用一次就进入新的一层，当最内层的函数执行完毕后，再一层一层地由里到外退出。"

  简要概括，如果一个函数在内部调用了自己，那么就可以之为递归。

二.对递归的理解

  

  递归包含两个要素：关系和出口（也就是说，形成递归的函数一定包含着某种规律，找到这种规律，再确定出口就可以确定一个递归）

  住：出口不一定只有一个（如：斐波那契数列有两个出口）

三.程序的实现

  一般需要先将递归函数出口的判断写在前面，然后再写函数的关系式

#include <stdio.h>

int f(int n)
{
    if (n == 1)
    {
        return 1;
    }
    else
    {
        return f(n - 1) + n;
    }
}

int main()
{
    printf("%d",f(100));
}

四.汉诺塔问题

  

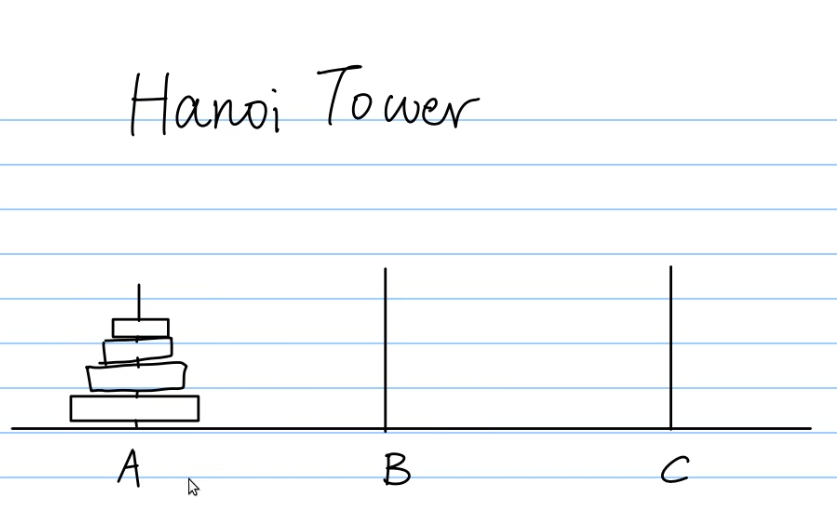
  (要求：将A中的盘子经过B全部移动到C中，并且在移动过程中大盘子不能在小盘子上面)

  解法：（1）当只有一个盘子时，直接将盘子从A移动到C即可，即move（A，C），这也就是递归的出口

     （2）当有多个盘子时，可以看成两部分，最下面的盘子是一部分，上面的所有盘子加起来是一部分，这样的话，就可以看做是上面所有盘子通过C移动到B，即hanoi（n-1,A,C,B），此                              时只需将A上的盘子移动到C即可，即move（A,C），接下来需要将B上剩下的n-1个盘子通过A移动到C上，所以再执行一次递归，hanoi(n-1,B,A,C)

#include <stdio.h>

void move(char a,char b)
{
    printf("%c -> %c\n",a,b);
}

void hanoi(int n,char A,char B,char C)
{
    if(n==1)
    {
        move(A,C);
    }
    else
    {
        hanoi(n-1,A,C,B);
        move(A,C);
        hanoi(n-1,B,A,C);
    }
}

int main()
{
    
    hanoi(3,'A','B','C');
    return 0;
}

五.总结

  递归的核心思想是找到出口以及规律，并将规律转换成函数表达式，而在我看来，找到规律的核心就是把部分看成整体（如汉诺塔问题，将上面的n-1个圆盘看成整体），然后对部分进行递归操作，最后得到整体的答案。