5.线性回归算法

1.本节重点知识点用自己的话总结出来，可以配上图片，以及说明该知识点的重要性

　　之于上节课学习的聚类，这节课的回归分析开篇先对这两种方法进行区别说明，以免后面学习混淆陷入理解误区：

 

 线性回归的定义：

 

 重温讲解了数组与矩阵的区别：

 

 对于机器运算中的误差差距，可用梯度下降法去解决：

　　　 

 

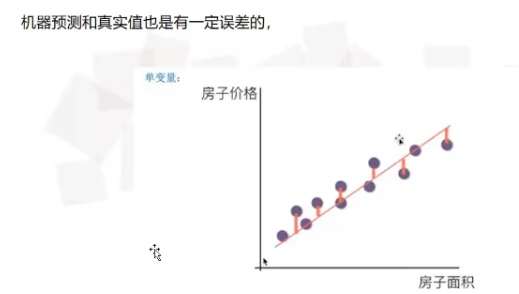
 　　线性回归对大量的观测数据进行处理，从而得到比较符合事物内部规律的数学表达式。也就是说寻找到数据与数据之间的规律所在，从而就可以模拟出结果，也就是对结果进行预测。解决的就是通过已知的数据得到未知的结果。在标准的线性回归的基础上，还可以扩展出更多的线性回归算法。

 

 2.思考线性回归算法可以用来做什么？（大家尽量不要写重复）　

　　基于线性回归算法的原理，在生活中应用例如可用对房价、股市走向、商品销售额、电影票房、不同类型视频流量导向等进行预测。

 

3.自主编写线性回归算法 ，数据可以自己造，或者从网上获取。（加分题）

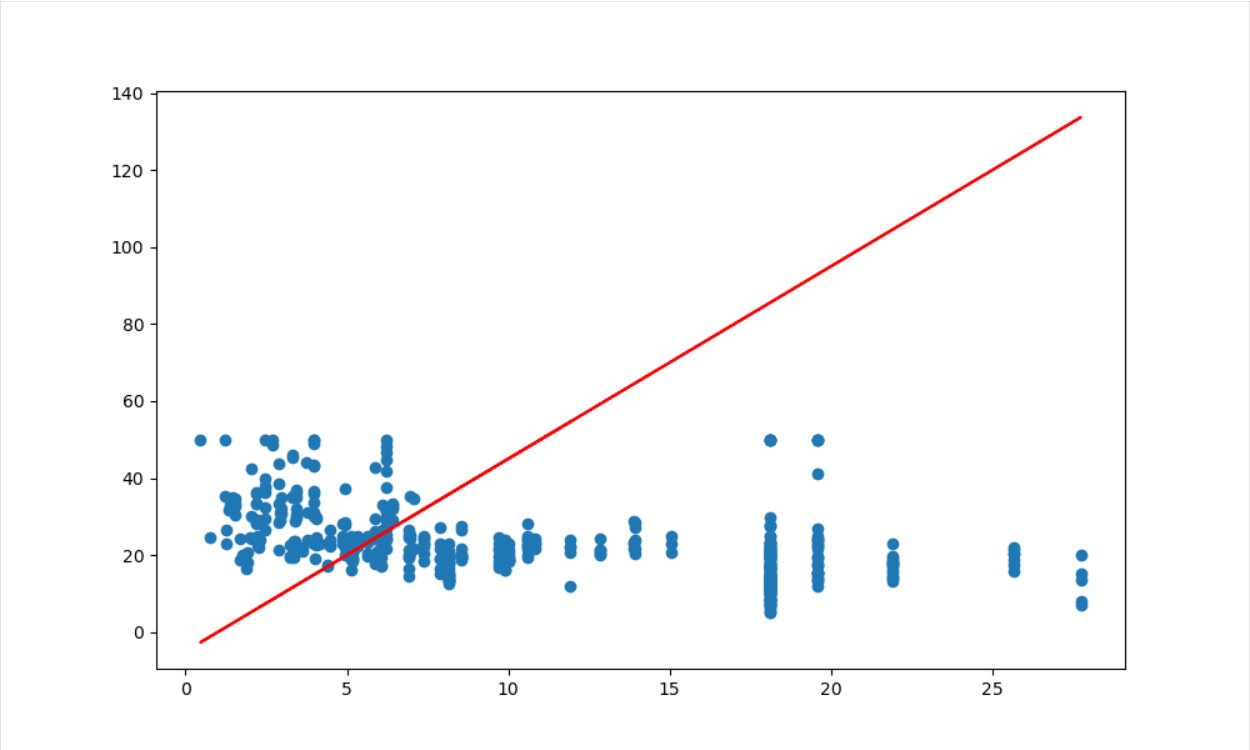
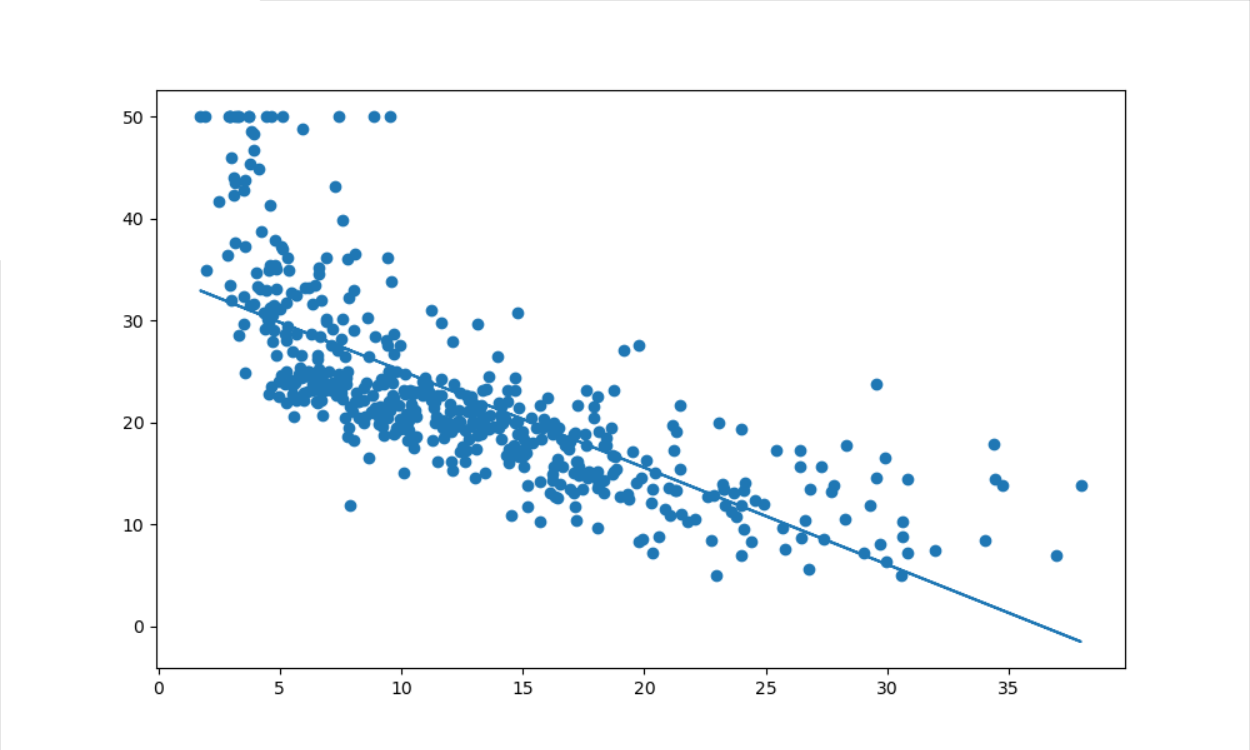
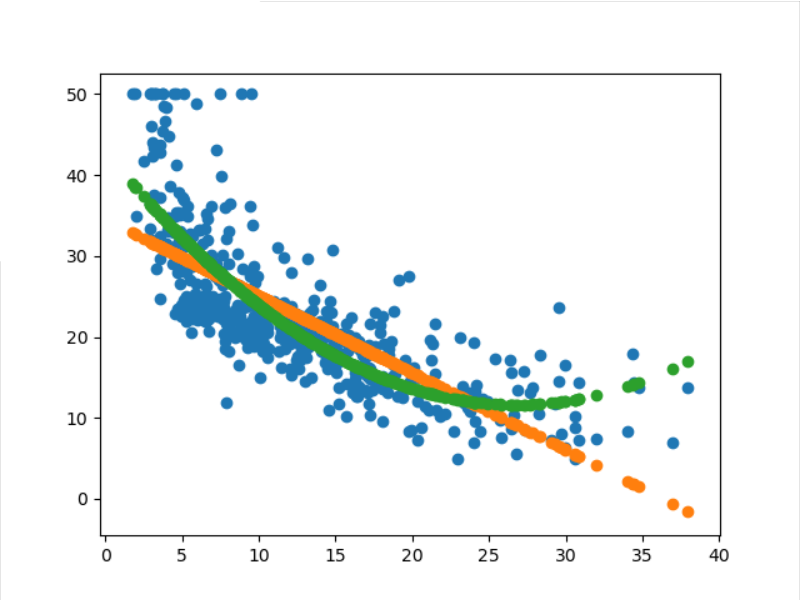
#导入房价数据集
from sklearn.datasets import load_boston
boston=load_boston()
boston.keys()

boston.data .shape
print(boston.DESCR)
boston.data
boston.target
boston.feature_names

import pandas as pd
df=pd.DataFrame(boston.data)
df

#一元线性回归模型，建立一个变量与房价之间的预测模型，并图形化显示。
import matplotlib.pyplot as plt
x=boston.data[:,2]     #下标2表示feature_names 的‘INDUS'
y=boston.target
plt.figure(figsize=(10,6))#指定显示图大小
plt.scatter(x,y)
plt.plot(x,5*x-5,'r')#回归线
plt.show()

from sklearn.linear_model import LinearRegression
lineR=LinearRegression()
lineR.fit(x.reshape(-1,1),y)  #对数据进行训练
lineR.coef_   #通过训练得到斜率
lineR.intercept_   #通过训练得到截距

#多元线性回归模型，建立13个变量与房价之间的预测模型，并检测模型好坏，并图形化显示检查结果。
from sklearn.linear_model import LinearRegression
lineR=LinearRegression()
lineR.fit(boston.data,y)  #对数据进行训练
lineR.coef_   #通过训练得到斜率
lineR.intercept_   #通过训练得到截距

x=boston.data[:,2]    
y=boston.target
plt.scatter(x,y)
plt.plot(x,4.63*x-36.49,'r')#回归线
plt.show()

#4一元多项式回归模型，建立一个变量与房价之间的预测模型，并图形化显示。
import matplotlib.pyplot as plt
x=boston.data[:,12].reshape(-1,1)
y=boston.target
plt.figure(figsize=(10,6))
plt.scatter(x,y)

from sklearn.linear_model import LinearRegression
lineR=LinearRegression()
lineR.fit(x,y)
y_pred=lineR.predict(x)
plt.plot(x,y_pred)
print(lineR.coef_,lineR.intercept_)
plt.show()
from sklearn.preprocessing import PolynomialFeatures
poly=PolynomialFeatures(degree=2)
x_poly=poly.fit_transform(x)
lrp=LinearRegression()
lrp.fit(x_poly,y)
y_poly_pred=lrp.predict(x_poly)
plt.scatter(x,y)
plt.scatter(x,y_pred)
plt.scatter(x,y_poly_pred)
plt.show()

结果依次展示：