1. 进制转换

题目描述

请你编一程序实现两种不同进制之间的数据转换。

输入格式

共三行，第一行是一个正整数，表示需要转换的数的进制 $n\ (2\le n\le 16)$，第二行是一个 $n$ 进制数，若 $n>10$ 则用大写字母 $\verb!A!\sim \verb!F!$ 表示数码 $10\sim 15$，并且该 $n$ 进制数对应的十进制的值不超过 $10^9$，第三行也是一个正整数，表示转换之后的数的进制 $m\ (2\le m\le 16)$。

输出格式

一个正整数，表示转换之后的 $m$ 进制数。

样例 #1

样例输入 #1

16
FF
2

样例输出 #1

11111111

点击查看代码

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
int a[6]={10,11,12,13,14,15};
void print(int n)
{
	if(n<10) cout<<n;
	else cout<<(char)((n-10)+'A');
}
void turn(ll sum,ll n)
{
	if(sum<n)
	{
		print(sum);
		return ;
	}
	turn(sum/n,n);
	print(sum%n);
}
void solve()
{
    int n;
    cin>>n;
    string s;
    cin>>s;
    ll ans=0;
    int len=s.size();
    for(int i=0;i<len;++i)//注意顺序从首到尾
    {
    	if(isdigit(s[i]))
    	ans=ans*n+s[i]-'0';//注意用数字的时候需要字符减‘0’
    	else 
    	ans=ans*n+a[s[i]-'A'];
    }
    //cout<<ans<<'\n';
    int t;
    cin>>t;
    turn(ans,t);
}
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    int T;
    T=1;
    while(T--)
    {
        solve();
    }
    return 0;
}

2.找筷子

题目描述

经过一段时间的紧张筹备，电脑小组的“RP 餐厅”终于开业了，这天，经理 LXC 接到了一个定餐大单，可把大家乐坏了！员工们齐心协力按要求准备好了套餐正准备派送时，突然碰到一个棘手的问题:筷子！

CX 小朋友找出了餐厅中所有的筷子，但遗憾的是这些筷子长短不一，而我们都知道筷子需要长度一样的才能组成一双，更麻烦的是 CX 找出来的这些筷子数量为奇数，但是巧合的是，这些筷子中只有一只筷子是落单的，其余都成双，善良的你，可以帮 CX 找出这只落单的筷子的长度吗？

输入格式

第一行是一个整数，表示筷子的数量 $n$。

第二行有 $n$ 个整数，第 $i$ 个整数表示第 $i$ 根筷子的长度 $a_i$。

输出格式

输出一行一个整数表示答案。

样例 #1

样例输入 #1

9
2 2 1 3 3 3 2 3 1

样例输出 #1

提示

数据规模与约定

对于 $30\%$ 的数据，保证 $n \leq 10^5$。
对于 $100\%$ 的数据，保证 $1 \leq n \leq 10^7 + 1$，$1 \leq a_i \leq 10^9$。

提示

请注意数据读入对程序效率造成的影响。
请注意本题的空间限制为 $4$ Mb。

点击查看代码

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
void solve()
{
    int n;
    cin>>n;
    int ans=0;
    int ai;
    for(int i=0;i<n;++i) {cin>>ai;ans^=ai;}
    cout<<ans<<'\n';
}
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    int T;
    T=1;
    while(T--)
    {
        solve();
    }
    return 0;
}

3. 高低位交换

题目描述

给出一个小于 $2^{32}$ 的非负整数。这个数可以用一个 $32$ 位的二进制数表示（不足 $32$ 位用 $0$ 补足）。我们称这个二进制数的前 $16$ 位为“高位”，后 $16$ 位为“低位”。将它的高低位交换，我们可以得到一个新的数。试问这个新的数是多少（用十进制表示）。

例如，数 $1314520$ 用二进制表示为 $0000\,0000\,0001\,0100\,0000\,1110\,1101\,1000$（添加了 $11$ 个前导 $0$ 补足为 $32$ 位），其中前 $16$ 位为高位，即 $0000\,0000\,0001\,0100$；后 $16$ 位为低位，即 $0000\,1110\,1101\,1000$。将它的高低位进行交换，我们得到了一个新的二进制数 $0000\,1110\,1101\,1000\,0000\,0000\,0001\,0100$。它即是十进制的 $249036820$。

输入格式

一个小于 $2^{32}$ 的非负整数

输出格式

将新的数输出

样例 #1

样例输入 #1

样例输出 #1

249036820

点击查看代码

#include<bits/stdc++.h>
using namespace std;
typedef unsigned int uint;
void solve()
{
    uint n;
    cin>>n;
    string s("");
    for(int i=31;i>=0;--i)
    {
    	int t=(n>>i&1);
    	s+=(char)(t+'0');
    }
    //cout<<s<<'\n';
    string s2;
    s2=s.substr(16);
    s=s.substr(0,16);//从0开始裁剪16位
    s2+=s;
    uint ans=0;
    for(int i=0;i<32;++i)
    ans=ans*2+(s2[i]-'0');
    cout<<ans<<'\n';
}
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    int T;
    T=1;
    while(T--)
    {
        solve();
    }
    return 0;
}

4. [NOIP2000 提高组] 进制转换

题目描述

我们可以用这样的方式来表示一个十进制数: 将每个阿拉伯数字乘以一个以该数字所处位置为指数,以 $10$ 为底数的幂之和的形式。例如 $123$ 可表示为 $1 \times 10^2+2\times 10^1+3\times 10^0$ 这样的形式。

与之相似的，对二进制数来说，也可表示成每个二进制数码乘以一个以该数字所处位置为指数,以 $2$ 为底数的幂之和的形式。

一般说来，任何一个正整数 $R$ 或一个负整数 $-R$ 都可以被选来作为一个数制系统的基数。如果是以 $R$ 或 $-R$ 为基数,则需要用到的数码为 $0,1,....R-1$。

例如当 $R=7$ 时,所需用到的数码是 $0,1,2,3,4,5,6$，这与其是 $R$ 或 $-R$ 无关。如果作为基数的数绝对值超过 $10$,则为了表示这些数码，通常使用英文字母来表示那些大于 $9$ 的数码。例如对 $16$ 进制数来说,用 $A$ 表示 $10$,用 $B$ 表示 $11$，用 $C$ 表示 $12$，以此类推。

在负进制数中是用 $-R $ 作为基数，例如 $-15$（十进制）相当于 $(110001)_{-2}$ （$-2$进制），并且它可以被表示为 $2$ 的幂级数的和数：

\[(110001)_{-2}=1\times (-2)^5+1\times (-2)^4+0\times (-2)^3+0\times (-2)^2+0\times (-2)^1 +1\times (-2)^0 \]

设计一个程序,读入一个十进制数和一个负进制数的基数, 并将此十进制数转换为此负进制下的数。

输入格式

输入的每行有两个输入数据。

第一个是十进制数 $n$。
第二个是负进制数的基数 $-R$。

输出格式

输出此负进制数及其基数，若此基数超过 $10$，则参照 $16$ 进制的方式处理。

样例 #1

样例输入 #1

30000 -2

样例输出 #1

30000=11011010101110000(base-2)

样例 #2

样例输入 #2

-20000 -2

样例输出 #2

-20000=1111011000100000(base-2)

样例 #3

样例输入 #3

28800 -16

样例输出 #3

28800=19180(base-16)

样例 #4

样例输入 #4

-25000 -16

样例输出 #4

-25000=7FB8(base-16)

提示

【数据范围】
对于 $100\%$ 的数据，$-20 \le R \le -2$，$|n| \le 37336$。

NOIp2000提高组第一题

点击查看代码

#include<bits/stdc++.h>
using namespace std;
void turn(int n,int r)
{
	if(n==0) return ;
	int k=n%r;
	if(k<0) {k-=r;n+=r;}
	turn(n/r,r);
	if(k<10)
	cout<<k;
	else cout<<(char)(k-10+'A');
}
void solve()
{
    int n,r;
    cin>>n>>r;
    cout<<n<<"=";
    turn(n,r);
    cout<<"(base"<<r<<')'<<'\n';
}
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    int T;
    T=1;
    while(T--)
    {
        solve();
    }
    return 0;
}

5.编号

题目描述

太郎有N只兔子，现在为了方便识别它们，太郎要给他们编号。兔子们向太郎表达了它们对号码的喜好，每个兔子i想要一个整数，介于1和Maxnumber[i]之间（包括1和Maxnumber[i]）。当然，每个兔子的编号是不同的。现在太郎想知道一共有多少种编号的方法。

你只用输出答案mod 1000000007即可。如果这是不可能的，就输出0.

输入格式

第一行是一个整数N。（1≤N≤50）

第二行N个整数Maxnumber[i]。（1≤Maxnumber[i]≤1000）

输出格式

一个整数

样例 #1

样例输入 #1

2
5 8

样例输出 #1

点击查看代码

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int p=1e9+7;
int a[1010],s[1010];
ll cal(int a,int b)
{
	ll ans=1;
	for(int i=a;i>=a-b+1;--i)
	{
		ans=ans*i%p;
	}
	return ans;
}
void solve()
{
    int n;
    cin>>n;
    int mi;
    for(int i=0;i<n;++i)
    {
    	cin>>mi;
    	a[mi]++;
    }
    int flag=1;
    for(int i=1;i<=1000;++i)
    {
    	s[i]=s[i-1]+a[i];
    	if(s[i]>i) flag=0;
    }
    //cout<<a[5]<<' '<<a[8]<<'\n';
    int sum=0;
    ll res=1;
    for(int i=1;i<=1000;++i)
    {
    	if(a[i]) {res*=cal(i-sum,a[i]);sum+=a[i];res%=p;}
    }
    cout<<res<<'\n';
}
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    int T;
    T=1;
    while(T--)
    {
        solve();
    }
    return 0;
}

6.[NOIP2016 提高组] 组合数问题

题目背景

NOIP2016 提高组 D2T1

题目描述

组合数 $\binom{n}{m}$ 表示的是从 $n$ 个物品中选出 $m$ 个物品的方案数。举个例子，从 $(1,2,3)$ 三个物品中选择两个物品可以有 $(1,2),(1,3),(2,3)$ 这三种选择方法。根据组合数的定义，我们可以给出计算组合数 $\binom{n}{m}$ 的一般公式：

\[\binom{n}{m}=\frac{n!}{m!(n-m)!} \]

其中 $n!=1\times2\times\cdots\times n$；特别地，定义 $0!=1$。

小葱想知道如果给定 $n,m$ 和 $k$，对于所有的 $0\leq i\leq n,0\leq j\leq \min \left ( i, m \right )$ 有多少对 $(i,j)$ 满足 $k|\binom{i}{j}$。

输入格式

第一行有两个整数 $t,k$，其中 $t$ 代表该测试点总共有多少组测试数据，$k$ 的意义见问题描述。

接下来 $t$ 行每行两个整数 $n,m$，其中 $n,m$ 的意义见问题描述。

输出格式

共 $t$ 行，每行一个整数代表所有的 $0\leq i\leq n,0\leq j\leq \min \left ( i, m \right )$ 中有多少对 $(i,j)$ 满足 $k|\binom{i}{j}$。

样例 #1

样例输入 #1

1 2
3 3

样例输出 #1

样例 #2

样例输入 #2

2 5
4 5
6 7

样例输出 #2

0
7

提示

【样例1说明】

在所有可能的情况中，只有 $\binom{2}{1} = 2$ 一种情况是 $2$ 的倍数。

【子任务】

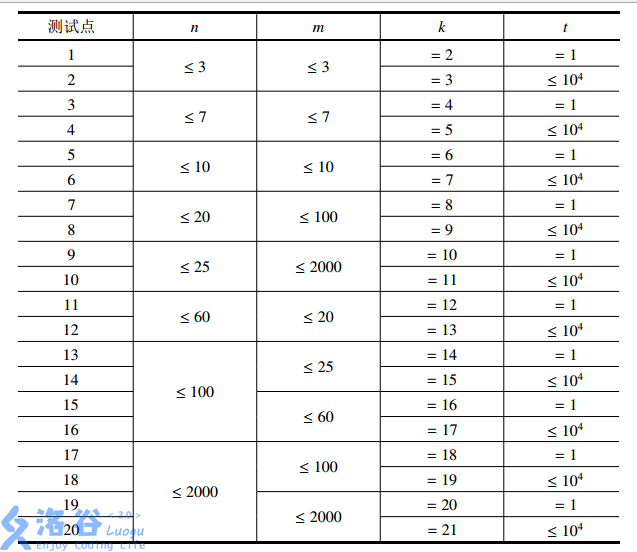
对于全部的测试点，保证 $0 \leq n, m \leq 2 \times 10^3$，$1 \leq t \leq 10^4$。

点击查看代码

#include<bits/stdc++.h>
using namespace std;
typedef unsigned int uint;
const int N=2010;
uint c[N][N];
uint dp[N][N];
int k;
void solve()
{
    int n,m;
    cin>>n>>m;
    int ans=0;
    for(int i=0;i<=n;++i)
    ans+=dp[i][min(i,m)];
    cout<<ans<<'\n';
}
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    int T;
    cin>>T>>k;
    for(int i=0;i<=2000;++i) c[i][0]=1%k;
    for(int i=1;i<=2000;++i)
     for(int j=1;j<=i;++j)
     c[i][j]=(c[i-1][j]+c[i-1][j-1])%k;
    for(int i=0;i<=2000;++i)
    {
    int tmp=0;
    for(int j=0;j<=i;++j)
    {
    if(c[i][j]==0) tmp++;
    dp[i][j]=tmp;	
    }
    }
    while(T--)
    {
        solve();
    }
    return 0;
}

7.直线交点数

题目描述

假设平面上有 $N$ 条直线，且无三线共点，那么这些直线一共能有多少不同的交点数？

输入格式

一行，一个整数 $N$，代表有 $N$ 条直线。

输出格式

一行，一个整数，表示方案总数。

样例 #1

样例输入 #1

样例输出 #1

提示

对于所有数据，满足 $1 \le N \le 25$。

点击查看代码

#include<bits/stdc++.h>
using namespace std;
const int N=1e4;
int h[N],res;
void rec(int p,int m)//p参数表示剩余多少条边没有考虑,m参数表示交点数
{
	if(p==0)//如果所有边已经分好类
	{
		if(!h[m]) h[m]=1,res++;
	}
	for(int i=p;i>=1;--i) //i表示下一组平行线的数量
	rec(p-i,m+i*(p-i));//一组数量为i的平行线可以新贡献i*(p-i)个交点
}
void solve()
{
    int n;
    cin>>n;
    rec(n,0);
    cout<<res<<'\n';
}
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    int T;
    //cin>>T;
    T=1;
    while(T--)
    {
        solve();
    }
    return 0;
}

8.车的攻击

题目描述

$N \times N$ 的国际象棋棋盘上有$K$ 个车，第$i$个车位于第$R_i$行，第$C_i$ 列。求至少被一个车攻击的格子数量。

车可以攻击所有同一行或者同一列的地方。

输入格式

第1 行，2 个整数$N,K$。

接下来K 行，每行2 个整数$R_i,C_i$。

输出格式

1 个整数，表示被攻击的格子数量。

样例 #1

样例输入 #1

3 2
1 2
2 2

样例输出 #1

提示

• 对于30% 的数据，$1 \le N \le 10^3; 1 \le K \le 10^3$；

• 对于60% 的数据，$1 \le N \le 10^6; 1 \le K \le 10^6$；

• 对于100% 的数据，$1 \le N \le 10^9; 1 \le K \le 10^6; 1 \le R_i , C_i \le N$。

点击查看代码

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=1e6;
int r[N<<1],c[N<<1];
int _hashr(int x)
{
	int t=(x%N+N)%N;
	while(r[t]&&r[t]!=x) t++;
	return t;
}
int _hashc(int x)
{
	int t=(x%N+N)%N;
	while(c[t]&&c[t]!=x) t++;
	return t;
}
void solve()
{
    int n,k;
    cin>>n>>k;
    int ri,ci;
    for(int i=0;i<k;++i)
    {
    cin>>ri>>ci;
    int t1=_hashr(ri); r[t1]=ri;
    int t2=_hashc(ci); c[t2]=ci;	
    }
    int sumr=0,sumc=0;
    for(int i=0;i<(N<<1);++i)
    {
    if(r[i]) sumr++;
    if(c[i]) sumc++;	
    }
    ll ans=(ll)(sumr+sumc)*n-(ll)sumr*sumc;
    cout<<ans<<'\n';
}
int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0);
    int T;
    //cin>>T;
    T=1;
    while(T--)
    {
        solve();
    }
    return 0;
}

posted on 2023-07-13 09:22 ruoye123456 阅读(90) 评论(0) 收藏举报

刷新页面返回顶部

1. 进制转换

题目描述

输入格式

输出格式

样例 #1

样例输入 #1

样例输出 #1

2.找筷子

题目描述

输入格式

输出格式

样例 #1

样例输入 #1

样例输出 #1

提示

数据规模与约定

提示

3. 高低位交换

题目描述

输入格式

输出格式

样例 #1

样例输入 #1

样例输出 #1

4. [NOIP2000 提高组] 进制转换

题目描述

输入格式

输出格式

样例 #1

样例输入 #1

样例输出 #1

样例 #2

样例输入 #2

样例输出 #2

样例 #3

样例输入 #3

样例输出 #3

样例 #4

样例输入 #4

样例输出 #4

提示

5.编号

题目描述

输入格式

输出格式

样例 #1

样例输入 #1

样例输出 #1

6.[NOIP2016 提高组] 组合数问题

题目背景

题目描述

输入格式

输出格式

样例 #1

样例输入 #1

样例输出 #1

样例 #2

样例输入 #2

样例输出 #2

提示

7.直线交点数

题目描述

输入格式

输出格式

样例 #1

样例输入 #1

样例输出 #1

提示

8.车的攻击

题目描述

输入格式

输出格式

样例 #1

样例输入 #1

样例输出 #1

提示

公告