洛谷P2911 Bovine Bones G 概率 O(1)解法

此题数据范围小，O(n^3)暴力可做。

O(1)做法灵感来自于“某爱好赌博的数学家发现两骰子点数之和为7的概率最大”的典故。

学习了此题的最高赞题解，进而得出本文解法。

 

首先考虑两个骰子的情况：

（下图引用自此题的最高赞题解，我自己懒得画了qwq）

观察可得：

①点数之和共s1+s2-1种情况，分别为2~s1+s2。

②点数之和出现次数最多的是min(s1,s2)+1~max(s1,s2)+1，共abs(s1-s2)+1种情况。

③次数-点数之和呈现出类似于正态分布的先增后减对称分布。

 

然后加入第三个骰子，将前两个骰子点数之和的所有情况作为行坐标（假设s1=s2=3），第三个骰子的点数作为列坐标：

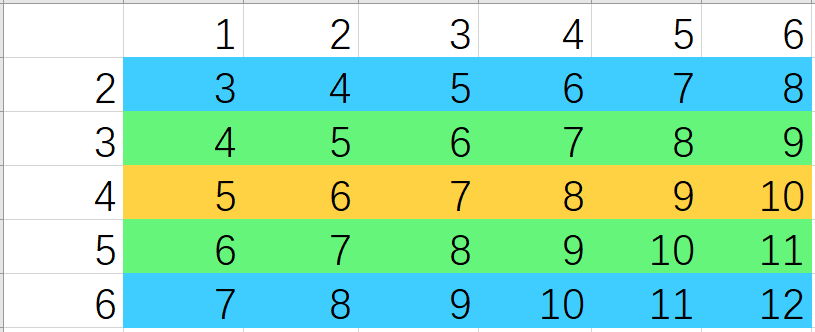
以不同颜色表示点数之和的出现次数。

观察可得：

①s3>=s1+s2-1时，从“经过左下角的对角线”到“经过右上角的对角线”（图中对应7~8）均为出现次数最多的，答案为其中的最小者s1+s2+1。

②不满足第一条但s3>abs(s1-s2)+1时，斜向条带可真包含上述的min(s1,s2)+1~max(s1,s2)+1段，最“靠近中间”的条带包含的所有行坐标的出现次数之和最大。当条带长度（即s3）与行坐标长度（即s1+s2-1）奇偶性相同时，条带可恰好处于行坐标的中间位置，答案为(((s1+s2-1)-s3)>>1)+(s3+2)；否则应选取最“靠近中间”的两者中较小者，答案为(((s1+s2-1)-(s3+1))>>1)+(s3+2)。

③不满足第二条时，条带位于min(s1,s2)+1~max(s1,s2)+1段之内，答案为其中的最小者min(s1,s2)+1。

代码：

#include<cstdio>
#include<iostream>
#include<cmath>
#include<algorithm>
#include<cstdlib>
#include<cstring>

using namespace std;

int s1,s2,s3;
int ans;

int main(){
    scanf("%d%d%d",&s1,&s2,&s3);
    if(s3>=s1+s2-1){
        ans=s1+s2+1;
    }
    else{
        if(s3>abs(s1-s2)+1){
            if((s3+s1+s2-1)&1){
                ans=(((s1+s2-1)-(s3+1))>>1)+(s3+2);
            }
            else{
                ans=(((s1+s2-1)-s3)>>1)+(s3+2);
            }
        }
        else{
            ans=min(s1,s2)+1;
        }
    }
    printf("%d\n",ans);
    
    return 0;
}