Splay 与 Link-Cut Tree 学习笔记（缺高级应用）

Splay 与 Link-Cut Tree 学习笔记

Splay 学习笔记

Splay 简介

个人感觉 Splay 没有 FHQ-Treap 用着舒服，代码也长很多，但是为了学 LCT，不得不学一下 Splay。

Splay（伸展树）是一种二叉查找树，通过不断地将节点旋转到根节点，使得整棵树仍满足二叉查找树的性质，并且能够保持平衡而不退化成链，由 Daniel Sleator 和 Robert Tarjan 发明。

Splay 结构

Splay 首先是一棵二叉查找树。

Splay 需要维护如下信息：

• \(rt\)：根节点。
• \(sz\)：节点个数。

同时，每个节点需要维护如下信息：

• \(fa\)：父亲节点。
• \({son}_{0/1}\)：左右子节点。
• \(val\)：权值。
• \(cnt\)：有几个数。
• \(sz\)：子树大小。

pushup 操作

pushup 用于更新节点信息。

void pushup(int u) {t[u].sz = t[t[u].son[0]].sz + t[t[u].son[1]].sz + t[u].cnt;}

get 操作

get 用于判断一个节点是它的父亲的哪个儿子。

bool get(int u) {return u == t[t[u].fa].son[1];}

rotate 操作

rotate 用于将一个节点上移一个位置，要满足二叉查找树性质。

有两种旋转：左旋和右旋。这里贺一张 OI Wiki 图片过来：

观察左侧图片到右侧图片的“右旋 \(2\)”过程，进行的操作如下：

• 将 \(2\) 的右儿子变为 \(1\) 的左儿子。
• 将 \(1\) 变为 \(2\) 的右儿子。
• 如果 \(1\) 有父亲，将原来 \(1\) 的位置换成 \(2\)。

容易发现这棵树的中序遍历不变，也就是说依然满足二叉查找树的性质。为了使每个节点维护的信息依然有效，需要依次对 \(1,2\) 进行 pushup 操作。

左旋同理。

void rotate(int u) {
	int f = t[u].fa, p = t[f].fa, id = get(u), idf = get(f);
	t[f].son[id] = t[u].son[id^1];
	if(t[u].son[id^1]) t[t[u].son[id^1]].fa = f;
	t[u].son[id^1] = f;
	t[f].fa = u;
	t[u].fa = p;
	if(p) t[p].son[idf] = u;
	pushup(f);
	pushup(u);
}

splay 操作

splay 用于将一个节点旋转到根，Splay 规定每访问一个节点都要进行这个操作。

分三种情况考虑：节点的父亲是根、节点和父亲的关系与父亲和祖父的关系相同、节点和父亲的关系与父亲和祖父的关系不同。

下面是这三种情况对应的图，为了理解这一操作，建议自行画图模拟一下（我画了一白板莫名爆字迹）：

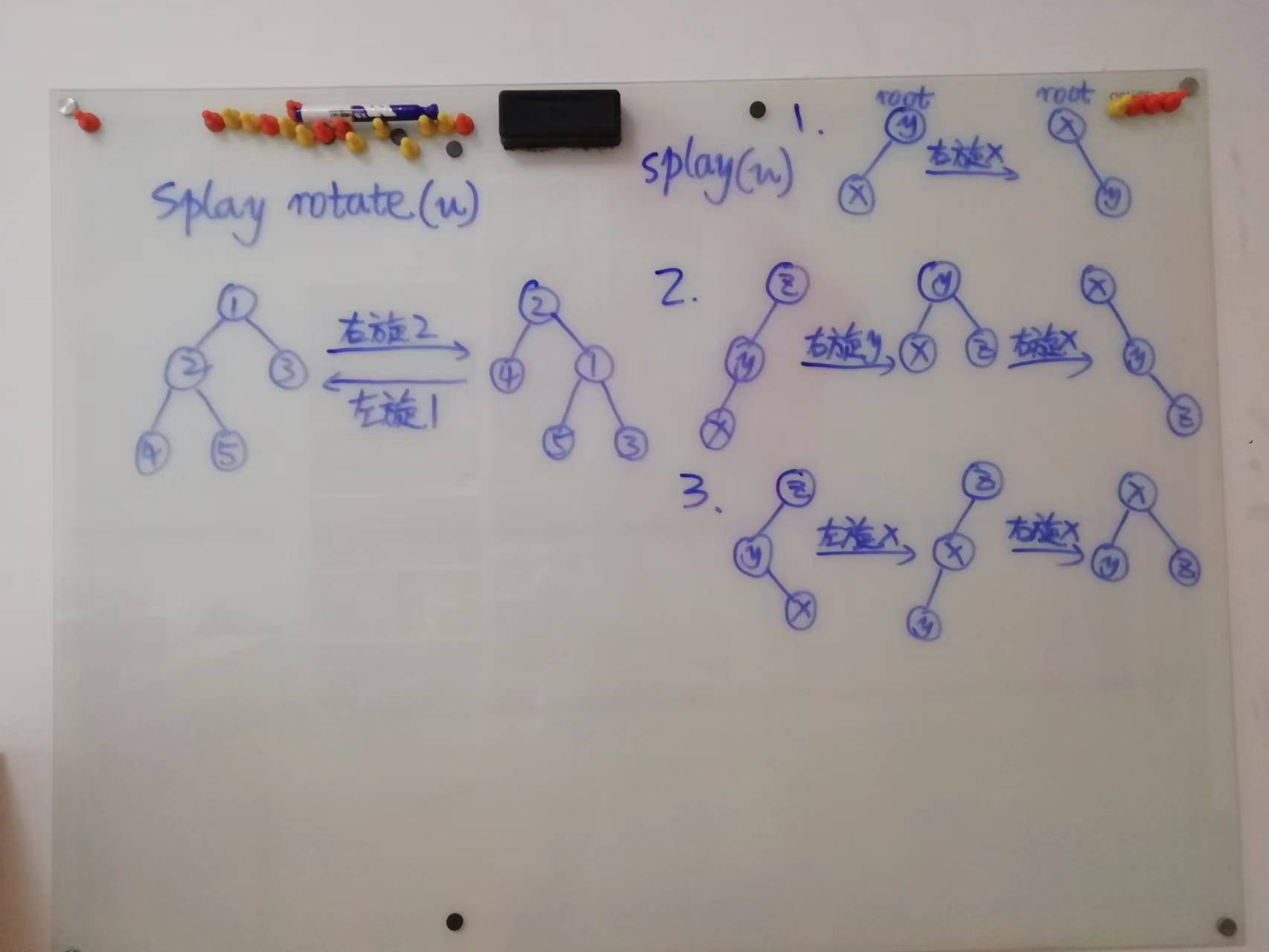
操作复杂但代码十分简短：

void splay(int u) {
	for(int f=t[u].fa;f=t[u].fa;rotate(u)) {
		if(t[f].fa) rotate(get(u) == get(f) ? f : u);
	}
	rt = u;
}

insert 操作

insert 用于插入一个数。

分几种情况：

• 如果树是空的，新建一个节点插进去即可。
• 否则根据二叉查找树性质找到要插入的位置，如果已经有节点，就把 \(cnt\) 加一然后 pushup，否则新建一个节点插进去。

记得进行 splay 操作。

void insert(int w) {
	int u = rt, f = 0;
	if(!u) {
		u = ++sz;
		t[u].val = w;
		t[u].cnt = 1;
		rt = u;
		pushup(u);
		return;
	}
	while(true) {
		if(t[u].val == w) {
			++t[u].cnt;
			pushup(u);
			pushup(f);
			splay(u);
			break;
		}
		f = u;
		u = t[u].son[t[u].val < w];
		if(!u) {
			u = ++sz;
			t[u].val = w;
			t[u].cnt = 1;
			t[u].fa = f;
			t[f].son[t[f].val < w] = u;
			pushup(u);
			pushup(f);
			splay(u);
			break;
		}
	}
}

rk 操作

rk 用于查询一个数的排名。

根据二叉查找树性质找到对应位置即可，记得记录有多少个数比查询的数小。

int rk(int w) {
	int u = rt, ans = 0;
	while(true) {
		if(w < t[u].val) {
			u = t[u].son[0];
			continue;
		}
		ans += t[t[u].son[0]].sz;
		if(w == t[u].val) {
			splay(u);
			return ans + 1;
		}
		ans += t[u].cnt;
		u = t[u].son[1];
	}
}

kth 操作

kth 用于查询排名为 \(k\) 的数。

根据二叉查找树性质找到对应位置即可。

int kth(int k) {
	int u = rt;
	while(true) {
		if(t[u].son[0] && k <= t[t[u].son[0]].sz) {
			u = t[u].son[0];
			continue;
		}
		k -= t[u].cnt + t[t[u].son[0]].sz;
		if(k <= 0) {
			splay(u);
			return t[u].val;
		}
		u = t[u].son[1];
	}
}

pre 操作和 suc 操作

pre 用于查询根节点的前驱，suc 用于查询根节点的后继。

查询任意数的前驱的做法为先插入，再查根节点前驱，最后删除，后继同理。

根节点的前驱就是左子树内最靠右的节点，后继同理。

int pre() {
	int u = t[rt].son[0];
	if(!u) return 0;
	while(t[u].son[1]) u = t[u].son[1];
	splay(u);
	return u;
}
int suc() {
	int u = t[rt].son[1];
	if(!u) return 0;
	while(t[u].son[0]) u = t[u].son[0];
	splay(u);
	return u;
}

erase 操作

erase 用于删除一个数。

首先将要删的数 splay 到根，然后分几种情况：

• 如果 \(cnt > 1\)，减小一并 pushup 即可。
• 如果既没有左儿子，又没有右儿子，那么直接删掉即可。
• 如果有其中一个儿子，将它放到根并删掉当前节点即可。
• 否则把前驱 splay 到根，并把右子树接到前驱上，然后删掉当前节点即可。

void erase(int w) {
	rk(w);
	if(t[rt].cnt > 1) {
		--t[rt].cnt;
		pushup(rt);
		return;
	}
	if(!t[rt].son[0] && !t[rt].son[1]) {
		t[rt] = Node();
		rt = 0;
		return;
	}
	if(!t[rt].son[0]) {
		int u = rt;
		rt = t[rt].son[1];
		t[rt].fa = 0;
		t[u] = Node();
		return;
	}
	if(!t[rt].son[1]) {
		int u = rt;
		rt = t[rt].son[0];
		t[rt].fa = 0;
		t[u] = Node();
		return;
	}
	int u = rt, x = pre();
	t[t[u].son[1]].fa = x;
	t[x].son[1] = t[u].son[1];
	t[u] = Node();
	pushup(rt);
}

普通平衡树

把以上部分结合起来就是了。

复杂度是 \(\mathcal O(n\log n)\)，但需要势能分析，我还不会，所以这里不证了= =

超长的代码：

// Problem: P3369 【模板】普通平衡树
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P3369
// Memory Limit: 128 MB
// Time Limit: 1000 ms
// 
// Powered by CP Editor (https://cpeditor.org)

//By: OIer rui_er
#include <bits/stdc++.h>
#define rep(x,y,z) for(int x=y;x<=z;x++)
#define per(x,y,z) for(int x=y;x>=z;x--)
#define debug printf("Running %s on line %d...\n",__FUNCTION__,__LINE__)
#define fileIO(s) do{freopen(s".in","r",stdin);freopen(s".out","w",stdout);}while(false)
using namespace std;
typedef long long ll;
const int N = 2e5+5;

int n;
template<typename T> void chkmin(T& x, T y) {if(x > y) x = y;}
template<typename T> void chkmax(T& x, T y) {if(x < y) x = y;}
struct Node {
	int fa, son[2], val, cnt, sz;
	Node() {fa = son[0] = son[1] = val = cnt = sz = 0;}
};
struct Splay {
	Node t[N];
	int rt, sz;
	void pushup(int u) {t[u].sz = t[t[u].son[0]].sz + t[t[u].son[1]].sz + t[u].cnt;}
	bool get(int u) {return u == t[t[u].fa].son[1];}
	void rotate(int u) {
		int f = t[u].fa, p = t[f].fa, id = get(u), idf = get(f);
		t[f].son[id] = t[u].son[id^1];
		if(t[u].son[id^1]) t[t[u].son[id^1]].fa = f;
		t[u].son[id^1] = f;
		t[f].fa = u;
		t[u].fa = p;
		if(p) t[p].son[idf] = u;
		pushup(f);
		pushup(u);
	}
	void splay(int u) {
		for(int f=t[u].fa;f=t[u].fa;rotate(u)) {
			if(t[f].fa) rotate(get(u) == get(f) ? f : u);
		}
		rt = u;
	}
	void insert(int w) {
		int u = rt, f = 0;
		if(!u) {
			u = ++sz;
			t[u].val = w;
			t[u].cnt = 1;
			rt = u;
			pushup(u);
			return;
		}
		while(true) {
			if(t[u].val == w) {
				++t[u].cnt;
				pushup(u);
				pushup(f);
				splay(u);
				break;
			}
			f = u;
			u = t[u].son[t[u].val < w];
			if(!u) {
				u = ++sz;
				t[u].val = w;
				t[u].cnt = 1;
				t[u].fa = f;
				t[f].son[t[f].val < w] = u;
				pushup(u);
				pushup(f);
				splay(u);
				break;
			}
		}
	}
	int rk(int w) {
		int u = rt, ans = 0;
		while(true) {
			if(w < t[u].val) {
				u = t[u].son[0];
				continue;
			}
			ans += t[t[u].son[0]].sz;
			if(w == t[u].val) {
				splay(u);
				return ans + 1;
			}
			ans += t[u].cnt;
			u = t[u].son[1];
		}
	}
	int kth(int k) {
		int u = rt;
		while(true) {
			if(t[u].son[0] && k <= t[t[u].son[0]].sz) {
				u = t[u].son[0];
				continue;
			}
			k -= t[u].cnt + t[t[u].son[0]].sz;
			if(k <= 0) {
				splay(u);
				return t[u].val;
			}
			u = t[u].son[1];
		}
	}
	int pre() {
		int u = t[rt].son[0];
		if(!u) return 0;
		while(t[u].son[1]) u = t[u].son[1];
		splay(u);
		return u;
	}
	int suc() {
		int u = t[rt].son[1];
		if(!u) return 0;
		while(t[u].son[0]) u = t[u].son[0];
		splay(u);
		return u;
	}
	void erase(int w) {
		rk(w);
		if(t[rt].cnt > 1) {
			--t[rt].cnt;
			pushup(rt);
			return;
		}
		if(!t[rt].son[0] && !t[rt].son[1]) {
			t[rt] = Node();
			rt = 0;
			return;
		}
		if(!t[rt].son[0]) {
			int u = rt;
			rt = t[rt].son[1];
			t[rt].fa = 0;
			t[u] = Node();
			return;
		}
		if(!t[rt].son[1]) {
			int u = rt;
			rt = t[rt].son[0];
			t[rt].fa = 0;
			t[u] = Node();
			return;
		}
		int u = rt, x = pre();
		t[t[u].son[1]].fa = x;
		t[x].son[1] = t[u].son[1];
		t[u] = Node();
		pushup(rt);
	}
}splay;

int main() {
	for(scanf("%d", &n);n;n--) {
		int op, x;
		scanf("%d%d", &op, &x);
		if(op == 1) splay.insert(x);
		else if(op == 2) splay.erase(x);
		else if(op == 3) printf("%d\n", splay.rk(x));
		else if(op == 4) printf("%d\n", splay.kth(x));
		else {
			splay.insert(x);
			printf("%d\n", splay.t[op==5?splay.pre():splay.suc()].val);
			splay.erase(x);
		}
	}
	return 0;
}

文艺平衡树

大概就是打 tag，然后 splay 要添加一个参数表示旋转到谁的儿子（或根），但我还没学，咕。

Link-Cut Tree

LCT 简介

Link-Cut Tree（LCT），又称 Link/Cut Tree，用来解决动态树问题。

LCT 中用的 Splay 是在 Splay 基础上进行扩展和改造过的。

动态树问题

动态树问题并不是指 LCT，而是这样的问题：维护一个森林，支持仍然满足森林性质的加减边操作，还要维护一些额外的信息（如：连通性、路径权值和等，虽然有些我还不会）。

实链剖分

我们常用的树剖是重链剖分，当然还有长链剖分，它们都是将点重新标号，来将树划分为若干个以链为单位的连续区间的并，从而使用线段树进行区间操作。

在动态树问题中，我们也希望进行一种链划分。到底需要什么链呢？我们希望划分的链可以自己指定，这样才方便求解。

对于一个节点，我们选定它的不超过一个儿子（可以不选）为实儿子，其他儿子为虚儿子。同时，我们称节点与实儿子相连的边为实边，与虚儿子相连的边为虚边，若干实边首尾相接形成实链。然后我们使用 Splay 来维护每一条实链的信息。

辅助树

上面说过，每棵 Splay 维护一条实链，那么原森林中用来维护每一棵树的若干棵 Splay 构成一棵辅助树。若干棵辅助树构成了 LCT，它们维护整个森林。

辅助树和 Splay 有如下性质：

• 辅助树由若干棵 Splay 构成，每棵 Splay 维护一条实链，且每棵 Splay 的中序遍历结果，与维护的这条实链从上到下依次对应。
• 原树的节点与辅助树中 Splay 节点一一对应。
• 一棵辅助树的各棵 Splay 不是独立的（不然就没有“一棵”辅助“树”一说了）。具体地，每棵 Splay 的根节点的父亲节点本应为空，但是 LCT 中每棵 Splay 的根节点的父亲节点指向原树中这条实链的链顶节点的父亲节点。也就是说，只有原树根节点所在 Splay 的根节点的父亲节点为空。这类父亲链接中，儿子的父亲链接指向父亲，但父亲没有一个儿子（特指左右儿子）指向儿子，通常被形象地描述为“儿子认父亲，父亲不认儿子”。
• 由于前面三条性质，我们不需要维护原树，只需要维护辅助树即可。一棵辅助树可以唯一确定一棵原树。（思考为什么？如何确定？在下文会回答）

注意：原树的根节点不等于辅助树的根节点，原树的父子关系也不等于辅助树的父子关系。

例如，下图是原树和辅助树的一个例子：

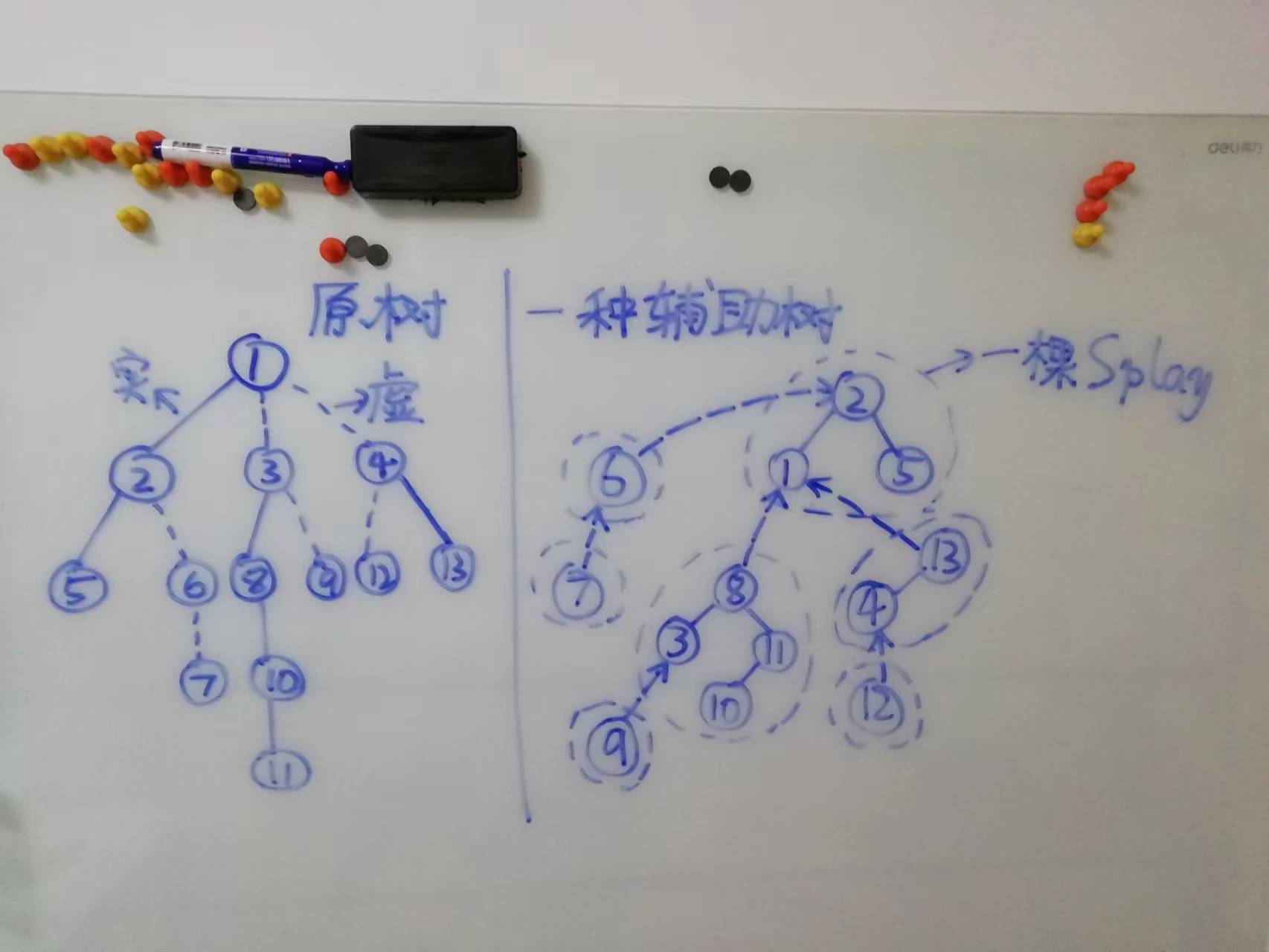
请观察上面三条性质在这棵辅助树中是怎么体现的。

为什么辅助树可以唯一确定原树？

我们可以给出构造方法。

每条实链就是一棵 Splay 的中序遍历，这个是很好求的。

考虑虚边，每条虚边对应一个单向的父亲链接，其中父亲就是虚边靠上的点。儿子虽然不是虚边靠下的点，但是不要忘记一棵 Splay 对应一条实链，虚边靠下的点显然就是实链顶端，也就是这棵 Splay 中序遍历的第一个点。

维护的信息

LCT 中的每个节点需要维护如下信息：

• \(fa\)：父亲节点（包含双向/单向两种）。
• \(tag\)：翻转标记（翻转整棵子树的左右儿子，下面会提到）。
• \({son}_{0/1}\)：左右子节点。
• 其他题目需要维护的信息（因题而异）。

一些前文已经提到的操作

这些是前文 Splay 部分已经提到的操作，这里一笔带过：

• pushup 用于更新节点信息（因题而异）。
• pushdown 用于下传翻转标记（也许还有其他标记，因题而异）。
• get 返回 \(-1\sim 1\) 的整数，用于判断节点是父亲的哪个儿子（或者是单向链接）。
• rotate 用于将一个节点上移一个位置，要满足二叉查找树性质。
• splay 用于将一个节点旋转到其所在 Splay 的根。

然后为了后面写着方便封装的一些：

• connect 用于创建一个父亲链接，同时规定儿子是哪个（左右或单向）。
• pushall 用于从上到下一层一层 pushdown 标记。
• reverse 用于翻转一棵子树。

注意代码实现略有不同，所以放一遍新的：

int get(int u) {
	if(son[fa[u]][0] == u) return 0;
	if(son[fa[u]][1] == u) return 1;
	return -1;
}
void connect(int u, int f, int tp) {
	fa[u] = f;
	if(tp >= 0) son[f][tp] = u;
}
void pushup(int u) { // 见洛谷 P3690 【模板】动态树（Link Cut Tree）
	xsum[u] = xsum[son[u][0]] ^ xsum[son[u][1]] ^ val[u];
}
void reverse(int u) {
	swap(son[u][0], son[u][1]);
	tag[u] ^= 1;
}
void pushdown(int u) {
	if(!tag[u]) return;
	if(son[u][0]) reverse(son[u][0]);
	if(son[u][1]) reverse(son[u][1]);
	tag[u] = 0;
}
void pushall(int u) {
	if(get(u) != -1) pushall(fa[u]);
	pushdown(u);
}
void rotate(int u) {
	int v = fa[u], w = fa[v], p = get(u), q = get(v);
	int c = son[u][p^1];
	connect(c, v, p);
	connect(v, u, p^1);
	connect(u, w, q);
	pushup(v);
	pushup(u);
}
void splay(int u) {
	pushall(u);
	for(;get(u)!=-1;rotate(u)) {
		int f = fa[u];
		if(get(f) != -1) rotate(get(u) == get(f) ? f : u);
	}
}

access 操作

access 操作是 LCT 最核心的操作。

access 用于打通一个节点到所在原树树根之间的实链，使得根节点到这个节点之间成为实链（在同一棵 Splay 中），与路径相连的其它边变为虚边。

实现方法是：

• 记当前节点为 \(u\)，另外令 \(v\gets 0\)。
• 把 \(u\) 转到 Splay 的根。
• 把 \(v\) 设置为 \(u\) 的右儿子。
• 更新节点 \(u\) 维护的信息。
• 令 \(v\gets u\)，同时令 \(u\gets {fa}_u\)，回到第二步直到 \(u=0\)。

不知道 OI Wiki 是什么写法还有返回值，我的 access 就只是进行操作，没有返回值。

void access(int u) {
	int v = 0;
	for(;u;v=u,u=fa[u]) {
		splay(u);
		son[u][1] = v;
		pushup(u);
	}
}

makeroot 操作

makeroot 操作是 LCT 的另一个核心操作。

makeroot 用于把一个点变为原树的根。

维护链信息时，一条链的深度可能无法一直递增（比如先上到 LCA 再下去），这时候就需要一个 makeroot 操作变换树形态。

实现方法是：

• 打通这个点到原树树根的实链。
• 将这个点旋转到 Splay 的根。
• 翻转这棵 Splay 的左右儿子。

为啥要翻转？原本这个点是实链底端，转到根后这棵 Splay 的右儿子就是空的了，翻转一下这个点就变为中序遍历的第一个点，也就是树根。

void makeroot(int u) {
	access(u);
	splay(u);
	reverse(u);
}

findroot 操作

findroot 用于找到一个点所在树树根的编号。

实现方法是：

• 先找到整棵辅助树的树根，就是先打通实链然后旋转到根，则原树树根就是中序遍历第一个，一直沿左儿子走就行。
• 为了保证复杂度，在查询后要把查到的节点旋转到根。

int findroot(int u) {
	access(u);
	splay(u);
	for(;son[u][0];u=son[u][0]) pushdown(u);
	splay(u);
	return u;
}

split 操作

split 用于拿出一棵 Splay，维护给定两点之间的路径。

实现方法是：

• 先把一个点变为原树树根。
• 然后打通另一个点到这个点的实链。
• 最后把另一个点旋转到根。

void split(int u, int v) {
	makeroot(u);
	access(v);
	splay(v);
}

link 操作

link 用于连接两个分属不同连通块的点。

实现方法是：

• 先通过 makeroot、findroot 判断是否连通，已经连通直接退出。
• makeroot 后直接把节点父亲指向另一个点即可。

bool link(int u, int v) {
	makeroot(u);
	if(findroot(v) == u) return 0;
	fa[u] = v;
	return 1;
}

cut 操作

cut 用于断掉一条边。

实现方法是：

• 先 findroot 判是否连通，不连通直接退出。
• 然后 split 出来这条路径，判断两个点在中序遍历上是否相邻，不相邻直接退出。判断方法是看父亲和右儿子。
• 否则把这条边断掉并更新节点信息。

bool cut(int u, int v) {
	if(findroot(u) != findroot(v)) return 0;
	split(u, v);
	if(fa[u] != v || son[u][1]) return 0;
	fa[u] = son[v][0] = 0;
	pushup(v);
	return 1;
}

LCT 维护树链信息 | 【模板】动态树

把以上部分结合起来就是了。

复杂度是 \(\mathcal O(n\log n)\)，但需要势能分析，我还不会，所以这里不证了= =

代码：

// Problem: P3690 【模板】动态树（Link Cut Tree）
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P3690
// Memory Limit: 128 MB
// Time Limit: 1000 ms
// 
// Powered by CP Editor (https://cpeditor.org)

//By: OIer rui_er
#include <bits/stdc++.h>
#define rep(x,y,z) for(int x=y;x<=z;x++)
#define per(x,y,z) for(int x=y;x>=z;x--)
#define debug printf("Running %s on line %d...\n",__FUNCTION__,__LINE__)
#define fileIO(s) do{freopen(s".in","r",stdin);freopen(s".out","w",stdout);}while(false)
using namespace std;
typedef long long ll;
const int N = 1e5+5;

int n, m, a[N];
template<typename T> void chkmin(T& x, T y) {if(x > y) x = y;}
template<typename T> void chkmax(T& x, T y) {if(x < y) x = y;}
struct LinkCutTree {
	int fa[N], val[N], xsum[N], tag[N], son[N][2];
	int get(int u) {
		if(son[fa[u]][0] == u) return 0;
		if(son[fa[u]][1] == u) return 1;
		return -1;
	}
	void connect(int u, int f, int tp) {
		fa[u] = f;
		if(tp >= 0) son[f][tp] = u;
	}
	void pushup(int u) {
		xsum[u] = xsum[son[u][0]] ^ xsum[son[u][1]] ^ val[u];
	}
	void reverse(int u) {
		swap(son[u][0], son[u][1]);
		tag[u] ^= 1;
	}
	void pushdown(int u) {
		if(!tag[u]) return;
		if(son[u][0]) reverse(son[u][0]);
		if(son[u][1]) reverse(son[u][1]);
		tag[u] = 0;
	}
	void pushall(int u) {
		if(get(u) != -1) pushall(fa[u]);
		pushdown(u);
	}
	void rotate(int u) {
		int v = fa[u], w = fa[v], p = get(u), q = get(v);
		int c = son[u][p^1];
		connect(c, v, p);
		connect(v, u, p^1);
		connect(u, w, q);
		pushup(v);
		pushup(u);
	}
	void splay(int u) {
		pushall(u);
		for(;get(u)!=-1;rotate(u)) {
			int f = fa[u];
			if(get(f) != -1) rotate(get(u) == get(f) ? f : u);
		}
	}
	void access(int u) {
		int v = 0;
		for(;u;v=u,u=fa[u]) {
			splay(u);
			son[u][1] = v;
			pushup(u);
		}
	}
	void makeroot(int u) {
		access(u);
		splay(u);
		reverse(u);
	}
	int findroot(int u) {
		access(u);
		splay(u);
		for(;son[u][0];u=son[u][0]) pushdown(u);
		splay(u);
		return u;
	}
	void split(int u, int v) {
		makeroot(u);
		access(v);
		splay(v);
	}
	bool link(int u, int v) {
		makeroot(u);
		if(findroot(v) == u) return 0;
		fa[u] = v;
		return 1;
	}
	bool cut(int u, int v) {
		if(findroot(u) != findroot(v)) return 0;
		split(u, v);
		if(fa[u] != v || son[u][1]) return 0;
		fa[u] = son[v][0] = 0;
		pushup(v);
		return 1;
	}
}LCT;

int main() {
	scanf("%d%d", &n, &m);
	rep(i, 1, n) scanf("%d", &LCT.val[i]);
	rep(i, 1, m) {
		int op, u, v;
		scanf("%d%d%d", &op, &u, &v);
		if(!op) {
			LCT.split(u, v);
			printf("%d\n", LCT.xsum[v]);
		}
		else if(op == 1) LCT.link(u, v);
		else if(op == 2) LCT.cut(u, v);
		else {
			LCT.splay(u);
			LCT.val[u] = v;
		}
	}
	return 0;
}

LCT 维护连通性质

https://www.luogu.com.cn/problem/P2147 和 https://www.luogu.com.cn/problem/P2542 ，但还不会。

LCT 维护边权

https://www.luogu.com.cn/problem/P4234 ，但还不会。

LCT 维护子树信息

https://www.luogu.com.cn/problem/P4219 ，但还不会。

咕咕咕

其实上面的有些会了，但没啥时间补笔记。