题解 P8390【[COI2021] MalnaRISC】

有趣的构造题。前段时间研究过排序网络，然后随机跳题跳到了这题，就来写了。

可以发现本题即要求构造一个足够优秀的排序网络。

不妨设 \(n=2^k\)，因为对于任意的 \(n\) 都可以在后面添加若干个 \(+\infty\) 转化为这种情形。

下文中规定区间 \([l,r]\) 表示 \(\{x\in\mathbb{Z}\mid l\le x\le r\}\)，规定序列 \(a\) 的倒序为 \(\overline{a}\)，规定两个序列 \(a,b\) 按顺序拼接为 \(a+b\)，称题面中一行代码为一次操作。

定义一个序列是 双调 的，当且仅当它先增后减或者先减后增。

Batcher 曾提出一个比较网络，用于将一个长度为 \(n\) 的双调序列 \(a\) 分为两个长度为 \(\frac{n}{2}\) 的双调序列 \(a_{\min},a_{\max}\)，并且 \(a_{\min}\) 的最大值不超过 \(a_{\max}\) 的最小值。这种比较网络的实现方式为：对于每个 \(i\in[1,\frac{n}{2}]\)，将 \(a_i\) 和 \(a_{i+\frac{n}{2}}\) 中更小的那个加入 \(a_{\min}\)，更大的那个加入 \(a_{\max}\)。称这个网络为 双调归并网络 ，显然这个网络所需操作次数 \(1\)。借助双调归并网络，我们可以通过 \(\log_2 n\) 次递归对任意长度为 \(n\) 的双调序列进行排序。

接下来考虑利用双调归并网络进行排序，我们需要解决输入不是双调序列的情形。显然长度为 \(2\) 的序列都是双调序列（甚至是单调序列）。假设我们已经解决规模为 \(\frac{n}{2}\) 的子问题，现在尝试解决规模为 \(n\) 的问题。将序列 \(a\) 从中间劈开得到两个序列 \(b,c\)，并且我们已经对 \(b,c\) 进行排序。显然 \(b+\overline{c}\) 是双调序列，将 \(b+\overline{c}\) 输入进双调归并网络即可将 \(a\) 排序。这种比较网络的实现方式为：将上文提到的 \(\log_2 n\) 层双调归并网络的最外层改为 \(a_i\) 和 \(a_{n+1-i}\) 配对，剩余不变。称这个网络为 双调排序网络 ，例如 \(n=8\) 时的双调排序网络如下图：（其中相邻的同种颜色为同一次操作，每个蓝色矩形框住的范围为一个改造后的双调归并网络）

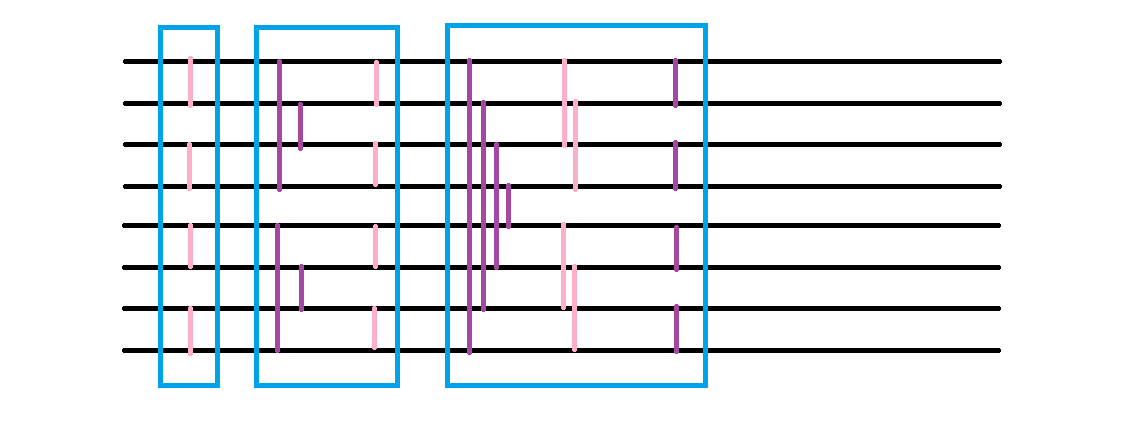
对序列 4 6 2 7 5 1 3 8 的每一次操作后结果如下：

INIT | 4 6 2 7 5 1 3 8
OP 1 | 4 6 2 7 1 5 3 8
OP 2 | 4 2 6 7 1 3 5 8
OP 3 | 2 4 6 7 1 3 5 8
OP 4 | 2 4 3 1 7 6 5 8
OP 5 | 2 1 3 4 5 6 7 8
OP 6 | 1 2 3 4 5 6 7 8

每一个双调归并网络的操作数为 \(\Theta(\log n)\)，一个双调排序网络由 \(\Theta(\log n)\) 个双调归并网络组成，因此总操作数为 \(\Theta(\log^2n)\)。在本题中每个测试点的操作次数依次为 \(6,10,10,15,21,21,28,28,28,28\)，可以通过本题。

参考代码：

//By: OIer rui_er
#include <bits/stdc++.h>
#define rep(x,y,z) for(int x=(y);x<=(z);x++)
#define per(x,y,z) for(int x=(y);x>=(z);x--)
#define debug(format...) fprintf(stderr, format)
#define fileIO(s) do{freopen(s".in","r",stdin);freopen(s".out","w",stdout);}while(false)
using namespace std;
typedef long long ll;

int n;
vector<vector<tuple<int, int>>> ans;
template<typename T> void chkmin(T& x, T y) {if(x > y) x = y;}
template<typename T> void chkmax(T& x, T y) {if(x < y) x = y;}

int main() {
	scanf("%d", &n);
	int m = 1;
	for(; m < n; m <<= 1);
	for(int l = 2; l <= m; l <<= 1) {
		int k = ans.size();
		ans.push_back({});
		for(int p = 1; p <= m; p += l) {
			for(int i = p, j = p + l - 1; i < j; i++, j--) {
				ans[k].emplace_back(i, j);
			}
		}
		for(int o = l >> 1; o >= 2; o >>= 1) {
			int k = ans.size();
			ans.push_back({});
			for(int p = 1; p <= m; p += o) {
				for(int i = p, j = p + (o >> 1); i < p + (o >> 1) && j < p + o; i++, j++) {
					ans[k].emplace_back(i, j);
				}
			}
		}
	}
	printf("%d\n", (int)ans.size());
	for(auto& i : ans) {
		for(auto& j : i) {
			int x = get<0>(j), y = get<1>(j);
			if(x > n || y > n) continue;
			printf("CMPSWP R%d R%d ", get<0>(j), get<1>(j));
		}
		puts("");
	}
	return 0;
}

参考文献：2002 年国家候选队论文 符文杰《排序网络》。