记一种奇异树剖方式
前言
我在 2025 年 7 月 21 日的杭电多校比赛中意外发现了本文中的奇异树剖方式,并利用它过了一道题。我猜测这种树剖方式肯定早已被前人发现,但是依然感觉很有意思。虽然它局限性很强,可能只在这一道题中有用,但还是写出来分享一下。
在阅读本文前需要掌握“树链剖分”的知识。
同步发布于 洛谷博客 。
upd:听说是 WC2024 论文吗,能重复造这个轮子这辈子也是有了。
它能用来做什么?
这里给出一道题目:
给定一棵 \(n\) 个节点的有根树,根节点为 \(rt\)。每个点 \(i\) 的初始点权为 \(a_i\)。
维护 \(m\) 个操作,操作包括:
- 给定 \(u,v,k\),将 \(u\) 到 \(v\) 路径上所有节点的点权增加 \(k\)。
- 给定 \(u,v\),求 \(u\) 到 \(v\) 路径上所有节点的点权和。
- 给定 \(u,k\),将 \(u\) 子树内所有节点的点权增加 \(k\)。
- 给定 \(u\),求 \(u\) 子树内所有节点的点权和。
- 给定 \(u,k\),将与 \(u\) 邻接的所有节点的点权增加 \(k\)。
- 给定 \(u\),求与 \(u\) 邻接的所有节点的点权和。
它与 P3384 【模板】重链剖分/树链剖分 的区别在于最后两种操作。
重儿子、轻儿子、重边、轻边、重链的定义与传统的轻重链剖分没有区别。不同点在于,当遍历所有节点进行编号时,采取以下的编号顺序:
- 先递归重链。
- 再给所有轻儿子编号。
- 最后递归轻边。
例如,下图是我草稿纸的一部分:
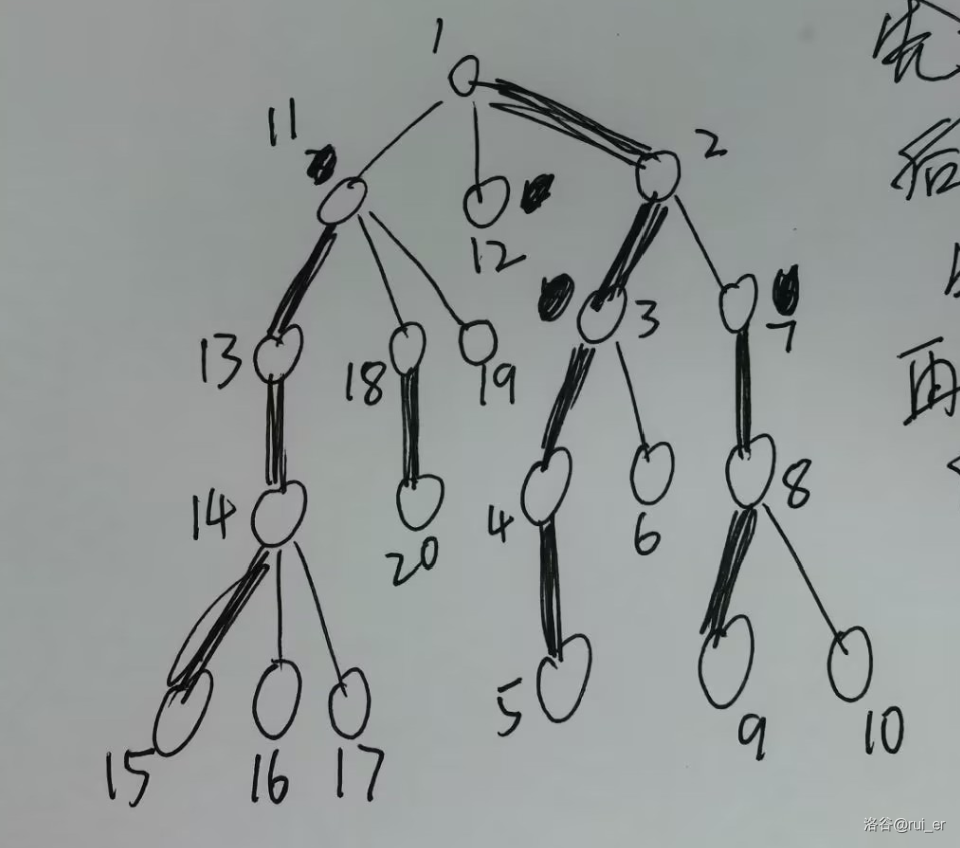
其中 \(11\sim 15\)、\(18\sim 20\) 的顺序跟正常树剖不一样,因为 \(1\) 递归重链子树内编号了 \(1\sim 10\),然后轻儿子编号为 \(11\sim 12\),再从 \(11\) 继续递归重链。
注意到这种树剖方式具有以下优美的性质:
- 一条重链,除了顶端节点编号可能不连续,其余节点编号连续。
- 一棵子树,除了根节点编号可能不连续,其余节点编号连续。
- 一个点的所有邻接点最多有三段连续区间,即父亲、重儿子、所有轻儿子。
于是可以在 \(O(\log n)\) 时间解决后四种操作,在 \(O(\log^2n)\) 时间解决前两种操作。
示例代码:(已在 P3384 【模板】重链剖分/树链剖分 提交通过,后两种操作已在杭电多校实验可行)
//By: OIer rui_er
#include <bits/stdc++.h>
#define rep(x, y, z) for(int x = (y); x <= (z); ++x)
#define per(x, y, z) for(int x = (y); x >= (z); --x)
#define debug(format...) fprintf(stderr, format)
#define fileIO(s) do {freopen(s".in", "r", stdin); freopen(s".out", "w", stdout);} while(false)
#define endl '\n'
using namespace std;
typedef long long ll;
mt19937 rnd(std::chrono::duration_cast<std::chrono::nanoseconds>(std::chrono::system_clock::now().time_since_epoch()).count());
int randint(int L, int R) {
uniform_int_distribution<int> dist(L, R);
return dist(rnd);
}
template<typename T> void chkmin(T& x, T y) {if(y < x) x = y;}
template<typename T> void chkmax(T& x, T y) {if(x < y) x = y;}
int mod;
inline unsigned int down(unsigned int x) {
return x >= mod ? x - mod : x;
}
struct Modint {
unsigned int x;
Modint() = default;
Modint(unsigned int x) : x(x) {}
friend istream& operator>>(istream& in, Modint& a) {return in >> a.x;}
friend ostream& operator<<(ostream& out, Modint a) {return out << a.x;}
friend Modint operator+(Modint a, Modint b) {return down(a.x + b.x);}
friend Modint operator-(Modint a, Modint b) {return down(a.x - b.x + mod);}
friend Modint operator*(Modint a, Modint b) {return 1ULL * a.x * b.x % mod;}
friend Modint operator/(Modint a, Modint b) {return a * ~b;}
friend Modint operator^(Modint a, int b) {Modint ans = 1; for(; b; b >>= 1, a *= a) if(b & 1) ans *= a; return ans;}
friend Modint operator~(Modint a) {return a ^ (mod - 2);}
friend Modint operator-(Modint a) {return down(mod - a.x);}
friend Modint& operator+=(Modint& a, Modint b) {return a = a + b;}
friend Modint& operator-=(Modint& a, Modint b) {return a = a - b;}
friend Modint& operator*=(Modint& a, Modint b) {return a = a * b;}
friend Modint& operator/=(Modint& a, Modint b) {return a = a / b;}
friend Modint& operator^=(Modint& a, int b) {return a = a ^ b;}
friend Modint& operator++(Modint& a) {return a += 1;}
friend Modint operator++(Modint& a, int) {Modint x = a; a += 1; return x;}
friend Modint& operator--(Modint& a) {return a -= 1;}
friend Modint operator--(Modint& a, int) {Modint x = a; a -= 1; return x;}
friend bool operator==(Modint a, Modint b) {return a.x == b.x;}
friend bool operator!=(Modint a, Modint b) {return !(a == b);}
};
const int N = 1e5 + 5;
typedef Modint mint;
int n, m, rt, fa[N], dis[N], sz[N], son[N], rngl[N], rngr[N], top[N], dfn[N], tms;
mint a[N], w[N];
vector<int> e[N];
void dfs1(int u, int f) {
fa[u] = f;
dis[u] = dis[f] + 1;
sz[u] = 1;
for(int v: e[u]) {
if(v == f) continue;
dfs1(v, u);
sz[u] += sz[v];
if(sz[v] > sz[son[u]]) son[u] = v;
}
}
void dfs2(int u, int tp) {
if(!fa[u]) dfn[u] = ++tms;
top[u] = tp;
w[dfn[u]] = a[u];
if(!son[u]) return;
dfn[son[u]] = ++tms;
dfs2(son[u], tp);
for(int v: e[u]) {
if(v == fa[u] || v == son[u]) continue;
dfn[v] = ++tms;
if(!rngl[u]) rngl[u] = dfn[v];
rngr[u] = dfn[v];
}
for(int v: e[u]) {
if(v == fa[u] || v == son[u]) continue;
dfs2(v, v);
}
}
struct SegTree {
mint sum[N << 2], tag[N << 2];
#define lc(u) (u << 1)
#define rc(u) (u << 1 | 1)
void build(mint* a, int u, int l, int r) {
tag[u] = 0;
if(l == r) {
sum[u] = a[l];
return;
}
int mid = (l + r) >> 1;
build(a, lc(u), l, mid);
build(a, rc(u), mid + 1, r);
sum[u] = sum[lc(u)] + sum[rc(u)];
}
void pushtag(int u, int l, int r, mint k) {
sum[u] += (r - l + 1) * k;
tag[u] += k;
}
void pushdown(int u, int l, int r) {
int mid = (l + r) >> 1;
pushtag(lc(u), l, mid, tag[u]);
pushtag(rc(u), mid + 1, r, tag[u]);
tag[u] = 0;
}
void modify(int u, int l, int r, int ql, int qr, mint k) {
if(ql > qr) return;
if(ql <= l && r <= qr) {
pushtag(u, l, r, k);
return;
}
pushdown(u, l, r);
int mid = (l + r) >> 1;
if(ql <= mid) modify(lc(u), l, mid, ql, qr, k);
if(qr > mid) modify(rc(u), mid + 1, r, ql, qr, k);
sum[u] = sum[lc(u)] + sum[rc(u)];
}
mint query(int u, int l, int r, int ql, int qr) {
if(ql > qr) return 0;
if(ql <= l && r <= qr) return sum[u];
pushdown(u, l, r);
int mid = (l + r) >> 1; mint ans = 0;
if(ql <= mid) ans += query(lc(u), l, mid, ql, qr);
if(qr > mid) ans += query(rc(u), mid + 1, r, ql, qr);
sum[u] = sum[lc(u)] + sum[rc(u)];
return ans;
}
}sgt;
void chainModify(int u, int v, mint k) {
while(top[u] != top[v]) {
if(dis[top[u]] < dis[top[v]]) swap(u, v);
if(u != top[u]) {
int w = son[top[u]];
sgt.modify(1, 1, n, dfn[w], dfn[u], k);
u = top[u];
}
sgt.modify(1, 1, n, dfn[u], dfn[u], k);
u = fa[u];
}
if(dis[u] < dis[v]) swap(u, v);
if(u == v) sgt.modify(1, 1, n, dfn[u], dfn[u], k);
else {
if(v == top[v]) {
sgt.modify(1, 1, n, dfn[v], dfn[v], k);
v = son[v];
}
sgt.modify(1, 1, n, dfn[v], dfn[u], k);
}
}
mint chainQuery(int u, int v) {
mint ans = 0;
while(top[u] != top[v]) {
if(dis[top[u]] < dis[top[v]]) swap(u, v);
if(u != top[u]) {
int w = son[top[u]];
ans += sgt.query(1, 1, n, dfn[w], dfn[u]);
u = top[u];
}
ans += sgt.query(1, 1, n, dfn[u], dfn[u]);
u = fa[u];
}
if(dis[u] < dis[v]) swap(u, v);
if(u == v) ans += sgt.query(1, 1, n, dfn[u], dfn[u]);
else {
if(v == top[v]) {
ans += sgt.query(1, 1, n, dfn[v], dfn[v]);
v = son[v];
}
ans += sgt.query(1, 1, n, dfn[v], dfn[u]);
}
return ans;
}
void treeModify(int u, mint k) {
sgt.modify(1, 1, n, dfn[u], dfn[u], k);
if(son[u]) sgt.modify(1, 1, n, dfn[son[u]], dfn[son[u]] + sz[u] - 2, k);
}
mint treeQuery(int u) {
mint ans = 0;
ans += sgt.query(1, 1, n, dfn[u], dfn[u]);
if(son[u]) ans += sgt.query(1, 1, n, dfn[son[u]], dfn[son[u]] + sz[u] - 2);
return ans;
}
void starModify(int u, mint k) {
if(fa[u]) sgt.modify(1, 1, n, dfn[fa[u]], dfn[fa[u]], k);
if(son[u]) sgt.modify(1, 1, n, dfn[son[u]], dfn[son[u]], k);
if(rngl[u]) sgt.modify(1, 1, n, rngl[u], rngr[u], k);
}
mint starQuery(int u) {
mint ans = 0;
if(fa[u]) ans += sgt.query(1, 1, n, dfn[fa[u]], dfn[fa[u]]);
if(son[u]) ans += sgt.query(1, 1, n, dfn[son[u]], dfn[son[u]]);
if(rngl[u]) ans += sgt.query(1, 1, n, rngl[u], rngr[u]);
return ans;
}
int main() {
ios::sync_with_stdio(false);
cin.tie(0); cout.tie(0);
cin >> n >> m >> rt >> mod;
rep(i, 1, n) cin >> a[i];
rep(i, 1, n - 1) {
int u, v;
cin >> u >> v;
e[u].push_back(v);
e[v].push_back(u);
}
dfs1(rt, 0);
dfs2(rt, rt);
sgt.build(w, 1, 1, n);
while(m--) {
int op;
cin >> op;
if(op == 1) {
int u, v; mint k;
cin >> u >> v >> k;
chainModify(u, v, k);
}
else if(op == 2) {
int u, v;
cin >> u >> v;
cout << chainQuery(u, v) << endl;
}
else if(op == 3) {
int u; mint k;
cin >> u >> k;
treeModify(u, k);
}
else if(op == 4) {
int u;
cin >> u;
cout << treeQuery(u) << endl;
}
else if(op == 5) {
int u; mint k;
cin >> u >> k;
starModify(u, k);
}
else {
int u;
cin >> u;
cout << starQuery(u) << endl;
}
}
return 0;
}
它还能用来做什么?
我也不知道。
看起来这个做法的可扩展性不高,如果它只能做这一道题,我也不会感到惊讶。
至少这个做法可以给我们提供一个思路:如果一道一脸树剖的题不好做,没准变换一下树剖方式,问题就迎刃而解了。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号