题解：P13343 [EGOI 2025] 一个弦线问题

我们把所有弦按照 \((a_i+b_i)\bmod(2n)\) 的值分为 \(2n\) 类，则两条弦平行当且仅当它们属于同一类中。当所有弦平行时，它们的类别都相同，我们称此时 \((a_i+b_i)\bmod(2n)\) 的值为这种方案的“旋转度”。

例如，题面中的这张图，左图的“旋转度”为 \(9\)，右图的“旋转度”为 \(5\)：

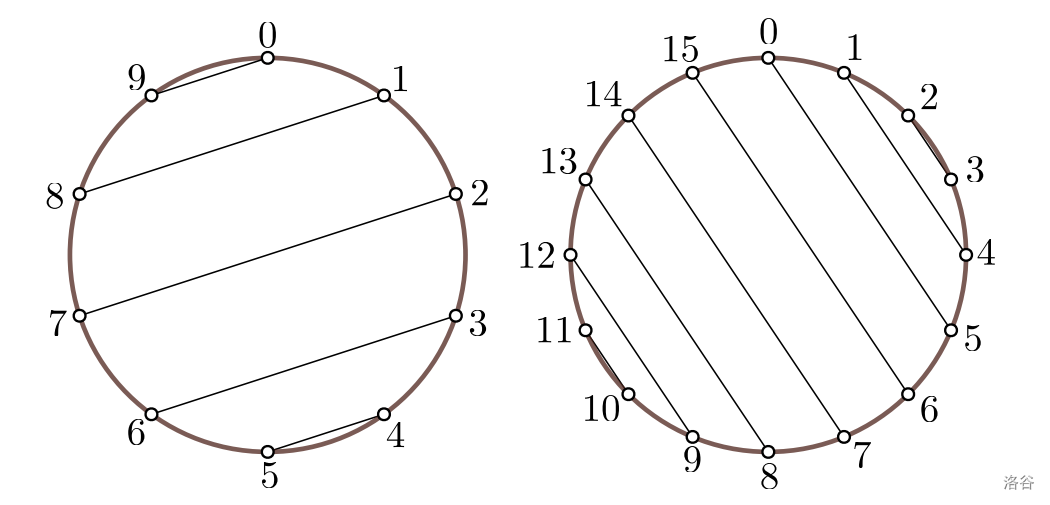
只有奇数才能成为合法的“旋转度”。若“旋转度”为偶数，会出现样例四的情况，显然不存在合法的方案。

我们大胆地猜测，对于任意一种合法的“旋转度”，最少操作次数为 \((a_i+b_i)\bmod(2n)\) 与“旋转度”不同的弦的个数。我们称这些弦为“不协调弦”，其余弦为“协调弦”。

所有“不协调弦”需要经过至少一次操作才能变为“协调弦”，而合法方案中的所有弦均为“协调弦”，因此最少操作次数一定不少于“不协调弦”的个数。下面构造性地证明这个下界一定能够取到：

• 定义性质 \(P\)：每个位置恰好连了一条弦。显然，初始状态具有性质 \(P\)。
• 随意挑选一条“不协调弦”，固定一个端点不变，将另一个端点移动到其他位置，使得这条弦变为“协调弦”。
• 移动到的那个位置恰好有一条弦，且必定为“不协调弦”。这是由初始状态具有性质 \(P\) 决定的。移动这个被占据的端点，使得这条弦也变为“协调弦”。
• 不断重复上一步，直到移动到的位置没有弦。此时的状态依然具有性质 \(P\)，且“不协调弦”的个数严格小于初始状态。
• 不断重复以上所有步骤，直到所有弦均为“协调弦”。“不协调弦”的个数一定可以在有限次重复之后减小至 \(0\)。容易注意到，每条“不协调弦”恰好被操作一次。

至此我们证明了这一结论，且直接按照以上步骤模拟即可给出构造方案。

我们枚举所有合法的“旋转度”，找出“不协调弦”个数最少的情况，并给出构造即可。

时间复杂度 \(O(n)\)。

//By: OIer rui_er
#include <bits/stdc++.h>
#define rep(x, y, z) for(int x = (y); x <= (z); ++x)
#define per(x, y, z) for(int x = (y); x >= (z); --x)
#define debug(format...) fprintf(stderr, format)
#define fileIO(s) do {freopen(s".in", "r", stdin); freopen(s".out", "w", stdout);} while(false)
#define endl '\n'
using namespace std;
typedef long long ll;

mt19937 rnd(std::chrono::duration_cast<std::chrono::nanoseconds>(std::chrono::system_clock::now().time_since_epoch()).count());
int randint(int L, int R) {
    uniform_int_distribution<int> dist(L, R);
    return dist(rnd);
}

template<typename T> void chkmin(T& x, T y) {if(y < x) x = y;}
template<typename T> void chkmax(T& x, T y) {if(x < y) x = y;}

template<int mod>
inline unsigned int down(unsigned int x) {
	return x >= mod ? x - mod : x;
}

template<int mod>
struct Modint {
	unsigned int x;
	Modint() = default;
	Modint(unsigned int x) : x(x) {}
	friend istream& operator>>(istream& in, Modint& a) {return in >> a.x;}
	friend ostream& operator<<(ostream& out, Modint a) {return out << a.x;}
	friend Modint operator+(Modint a, Modint b) {return down<mod>(a.x + b.x);}
	friend Modint operator-(Modint a, Modint b) {return down<mod>(a.x - b.x + mod);}
	friend Modint operator*(Modint a, Modint b) {return 1ULL * a.x * b.x % mod;}
	friend Modint operator/(Modint a, Modint b) {return a * ~b;}
	friend Modint operator^(Modint a, int b) {Modint ans = 1; for(; b; b >>= 1, a *= a) if(b & 1) ans *= a; return ans;}
	friend Modint operator~(Modint a) {return a ^ (mod - 2);}
	friend Modint operator-(Modint a) {return down<mod>(mod - a.x);}
	friend Modint& operator+=(Modint& a, Modint b) {return a = a + b;}
	friend Modint& operator-=(Modint& a, Modint b) {return a = a - b;}
	friend Modint& operator*=(Modint& a, Modint b) {return a = a * b;}
	friend Modint& operator/=(Modint& a, Modint b) {return a = a / b;}
	friend Modint& operator^=(Modint& a, int b) {return a = a ^ b;}
	friend Modint& operator++(Modint& a) {return a += 1;}
	friend Modint operator++(Modint& a, int) {Modint x = a; a += 1; return x;}
	friend Modint& operator--(Modint& a) {return a -= 1;}
	friend Modint operator--(Modint& a, int) {Modint x = a; a -= 1; return x;}
	friend bool operator==(Modint a, Modint b) {return a.x == b.x;}
	friend bool operator!=(Modint a, Modint b) {return !(a == b);}
};

const int N = 2e5 + 5;

int n, a[N][2], bel[N], cnt[N], ok[N];

int main() {
    ios::sync_with_stdio(false);
    cin.tie(0); cout.tie(0);
    cin >> n;
    rep(i, 0, n - 1) {
        cin >> a[i][0] >> a[i][1];
        bel[a[i][0]] = bel[a[i][1]] = i;
        ++cnt[(a[i][0] + a[i][1]) % (2 * n)];
    }
    int ans = n + 1, rem = -1;
    for(int r = 1; r <= 2 * n; r += 2) {
        if(n - cnt[r] < ans) {
            ans = n - cnt[r];
            rem = r;
        }
    }
    cout << ans << endl;
    rep(i, 0, n - 1) if((a[i][0] + a[i][1]) % (2 * n) == rem) ok[i] = 1;
    rep(i, 0, n - 1) {
        if(!ok[i]) {
            int u = i, c = 0;
            while(true) {
                int pos = (2 * n + rem - a[u][c]) % (2 * n);
                int v = bel[pos];
                cout << u << " " << a[u][c ^ 1] << " " << pos << endl;
                ok[u] = 1;
                bel[pos] = u;
                bel[a[u][c ^ 1]] = -1;
                if(v == -1) break;
                u = v;
                c = a[v][0] == pos ? 1 : 0;
            }
        }
    }
    return 0;
}