并查集判断(DSU)二分图

并查集(DSU)判断二分图

题目链接

二分图

性质

• 当且仅当图中不存在奇数环

偶数环时

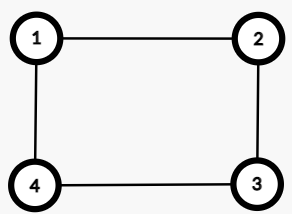
可以扭成这样

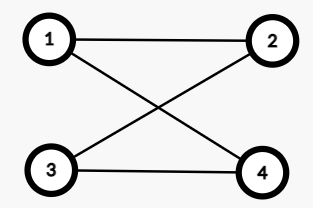
但奇数环则不可以

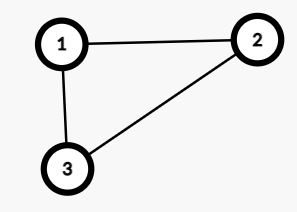
从染色法的角度来考虑：假设一个二分图中左边标号为1，右边标号为2。
则对于一个环来说 1 -> 2 -> 3 -> 4 -> ... -> n, 假设当前1的标号为1，根据二分图的定义，和1相连的点的标号应该为2，则2的标号为2，同理3的标号为1,4的标号为2，如此进行，最终如果环的边数为奇数，最终的1会被认为既属于1又属于2，如下图：

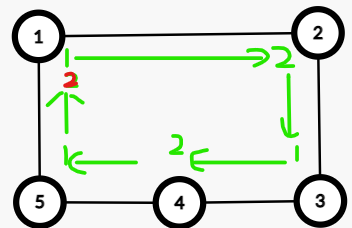
染色法判断二分图

做一遍bfs

并查集判断二分图

struct DSU {
    vector<int> p;
    DSU(int n) {
        p.resize(n + 1, 0);
        for (int i = 1; i <= n; i++) p[i] = i;
    }
    int find(int x) {
        return x == p[x] ? x : p[x] = find(p[x]);
    }
    void merge(int x, int y) {
        x = find(x);
        y = find(y);
        if (x != y) p[x] = y;
    }
};
int main() {
    int n, m;
    cin >> n >> m;
    DSU d(n * 2);
    for (int i = 1; i <= m; i++) {
        int u, v;
        cin >> u >> v;
        d.merge(u, n + v);
        d.merge(u + n, v);
    }
    bool f = true;
    for (int i = 1; i <= n; i++) {
        if (d.find(i) == d.find(i + n)) {
            f = false;
        }
    }
    puts(f ? "Yes" : "No");
    return 0;
}