La Salle-Pui Ching Programming Challenge 培正喇沙編程挑戰賽 2017

练习

题目来源

A - Ambiguous Datas

题意

定义一年\(M\)个月，每个月\(Di\)天，现在日期有两种表达方式dd/mm/year 和 mm/dd/year, 这样会产生歧义，例如， 1/2/12就是歧义的，
而1/13/12不是歧义的。现在给 \(M\) 和 \(D_1, D_2, D_3...D_m\),问如何排列D, 可以使歧义天数最少。

分析

对于第i月，他产生歧义的天数范围是 1 - min(D_i, M), 对于这个区间，容易想到，要求出该区间内的大于i的个数，因为i与j歧义，首先满足\(1 \leq j \leq M 且 D_j \geq i\), 所以要尽可能的减少区间的贡献，考虑将序列升序排列，一定更优。

做法：sort + 找区间贡献(二分找大于i的最小的)

细节：注意要刨去\(D_i \geq i\)

const int N = 100010;
ll d[N], n, m;
ll ans;
void solve() {
	cin >> n;
	for (int i = 1; i <= n; i++) cin >> d[i], m = max(m, d[i]);
	sort(d + 1, d + n + 1);
	for (int i = 1; i <= n; i++) {
		int l = 0, r = min(n, d[i]) + 1;
		while (l < r) {
			int mid = (l + r) / 2;
			if (d[mid] >= i) r = mid;
			else l = mid + 1;
		}
		ans += (min(n, d[i]) - l + 1) - (d[i] >= i);
	}
	cout << ans << '\n';
}

B - Bacteria Experiment

题意

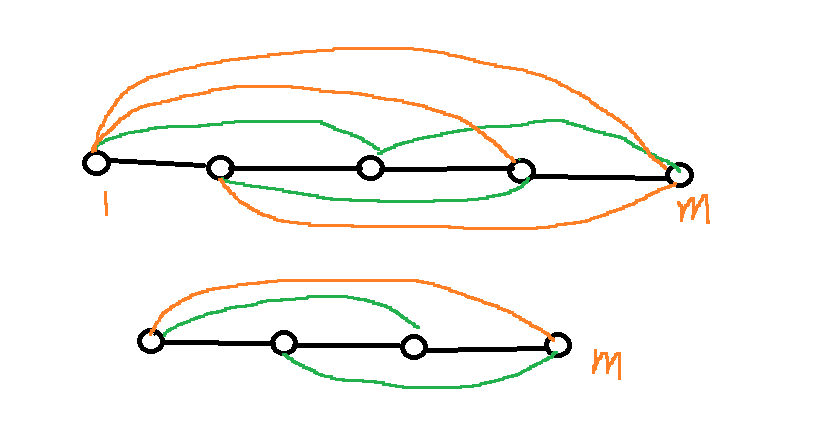
给一棵树，每过一个小时，u和v会连一条边，当存在点e，满足E(u, e), E(v, e)存在(即u-e, v-e直接相连，u,v没有边相连)。问这棵树经过几个小时，这个树会变成一个完全图。

分析

每次操作都是同时进行，所以我们只需要考虑最长的链，即找到树的直径，当这条直径完全两两相连时，树上的其他链均完成了这个过程。并且我们考虑一条长度为m的树链，可以发现，每过一个小时，路径长度变为原来的1/2，故，我们的答案为(\(2^{ans} >= dist\))最小的ans。

const int N = 500010;
int n, cnt;
VI e[N];
bool st[N];
PII bfs(int start) {
	PII ans = {0, 0};
	queue<PII> q;
	q.push({0, start});
	memset(st, 0, sizeof st);
	while (!q.empty()) {
		auto [d, u] = q.front(); q.pop();
		if (st[u]) continue;
		st[u] = 1;
		for (auto v : e[u]) {
			if (!st[v]) {
				q.push({d + 1, v});
				if (d + 1 > ans.fi) ans = {d + 1, v};
			}
		}
	}
	return ans;
}
 
void solve() {
	cin >> n;
	for (int i = 1; i < n; i++) {
		int u, v;
		cin >> u >> v;
		e[u].pb(v);
		e[v].pb(u);
	}
	auto a = bfs(1);
	auto b = bfs(a.se);
	int d = b.fi;
	int ans = 0;
	while ((1 << ans) < d) ans++;
	cout << ans << '\n';
}

I - Inverted Signs

题意

给定一个整数序列a, 要求值 \(H = \sum_{i=2}^{N}(|a[i]-a[i-1]|)\),现在可以进行一次操作，选择一个区间[L, R],进行翻转，要求翻转后使H的值最小，问最小的H。

分析

[L, R]区间内部的差值不会变，变得只是a[L] - a[L-1]和a[R+1] - a[R],所以做法很简单，就是对于i，求出i翻转后的对答案的贡献，并且维护最小的和次小的贡献即可。

注意： 因为可以翻转整个序列，所以求出贡献要对0取min。

const int N = 1000010;
int a[N], n;
ll ans;
void solve() {
    cin >> n;
    PII mx = {1e9, 0}, mx2 = {0, 0};
    for (int i = 1; i <= n; i++) {
        cin >> a[i];
        if (i > 1) {
            int x = abs(a[i] - a[i - 1]);
            int y = abs(-a[i] - a[i - 1]);
            ans += x;
            if (y - x < mx.fi) {
                mx2 = mx;
                mx = {y - x, i};
            } else if (y - x < mx2.fi) {
            	mx2 = {y - x, i};
            }
        }
    }
    if (n == 1) ans = 0, mx = {0, 0};
    cout << ans + min(0, mx.fi) + min(0, mx2.fi) << '\n';
}

H - Hit!

题意

给两个有重叠部分的圆，在重叠部分任意找到一点输出

分析

容易想到圆心连线上一定可以找到这个点，故直接二分圆心线段，当前点不在圆a内时,向圆b收缩区间，反之向a收缩

typedef pair<db, db> Point;
const db eps = 1e-5;
Point a, b;
struct Circle {
	Point mi;
	db r;
};
 
db dis(Point a, Point b) {
	return sqrt(1.0*(a.fi-b.fi)*(a.fi-b.fi)+1.0*(a.se-b.se)*(a.se-b.se));
}
 
bool in(Circle x, Point a) {
	return dis(a, x.mi) < x.r;
}
 
Point Hf(Point a, Point b) {
	return Point{(a.fi+b.fi)/2.0, (a.se+b.se)/2.0};
}
 
void solve() {
	Circle a, b;
	db x, y, r;
	cin >> x >> y >> r;
	a.mi = {x, y};
	a.r = r;
	cin >> x >> y >> r;
	b.mi = {x, y};
	b.r = r;
	Point L = a.mi, R = b.mi;
	while(dis(L, R) >= EPS) {
		Point mid = Hf(L, R);
		if (in(a, mid) && in(b, mid)) {
			printf("%.12f %.12f\n", mid.fi, mid.se);
			return ;
		}
		if (in(a, mid)) L = mid;
		else R = mid;
	}
	if (in(a, L) && in(b, L)) printf("%.12f %.12f\n", L.fi, L.se);
}

C - Cheering

题意

找出"LSC"和"PCMS"个数。

分析

使用string.find(string)函数

void solve() {
	string s; cin >> s;
	string a = "LSC", b = "PCMS";
	int c = 0;
	while (s.find(a) != -1) {
		int t = s.find(a);
		s[t] = '#';
		c++;
	}
	while (s.find(b) != -1) {
		int t = s.find(b);
		s[t] = '#';
		c--;
	}
	if (c > 0) cout << a << '\n';
	if (c < 0) cout << b << '\n';
	if (c == 0) cout << "Tie\n";
}