Linux C进阶 —— 浮点数表示（IEEE标准754）

1. IEEE标准754

    IEEE标准754制订了表示浮点数的标准， 解决了浮点数在不同机器上的可移植性。该标准使用

            F = (-1)^s * M * 2^E

    形式来表示一个实数。

    s: 表示符号， 1为负实数， 0为正实数；

    M: 表示尾数，是一个二进制小数；

    E: 表示阶码，对浮点数加权。为正数时，意为将M的小数点右移E位；为负数时，意为将M的小数点左移 |E| 位。

    IEEE标准754包含2中常见的标准浮点格式R32.23（如图1）和R64.52(如图2）。图中s为符号位；exp为阶码E的编码；frac为小数部分，是对尾数M的编码。

    

                                  图1 单精度32位浮点格式R32.23                                            

 

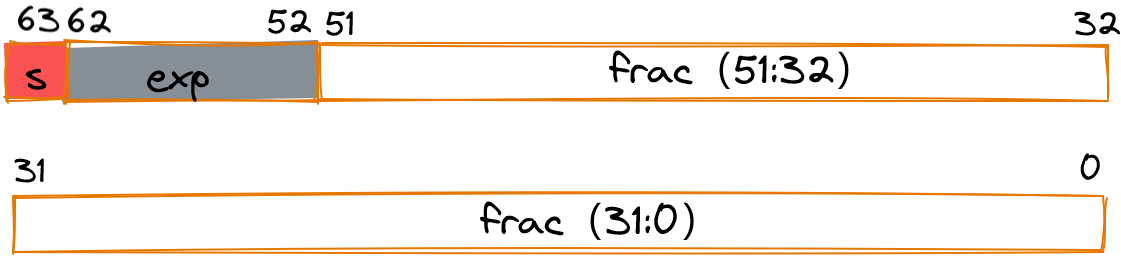
 图2 双精度64位浮点格式R64.52

        根据exp的值，被编码的实数分3中不同的情况，以单精度格式RS32.23为例：

（1）规格化的（exp不为全0、不为全1）

     E = exp - 127；

     M = 1 + frac （尾数M的开头1不会编码到frac，而作为隐含数字）

（2）非规格化的(exp 为全0）

      E = 1 - 127；

     M = frac

     该格式有2个作用， 一是用来表示±0.0， 二是用来表示非常接近0的数。

（3-a）无穷大(exp 为全1， frac 为0）

     s = 1时， 为-∞ 的编码；  

     s = 0时， 为+∞ 的编码。

（3-b）NaN(Not a Number， exp 为全1， frac 不为0）

 

2. 浮点数编码举例

（1）小数的二进制转换

      循环取小数部分乘以2，取积的整数部分，直到积等于1.以0.375为例，如下图

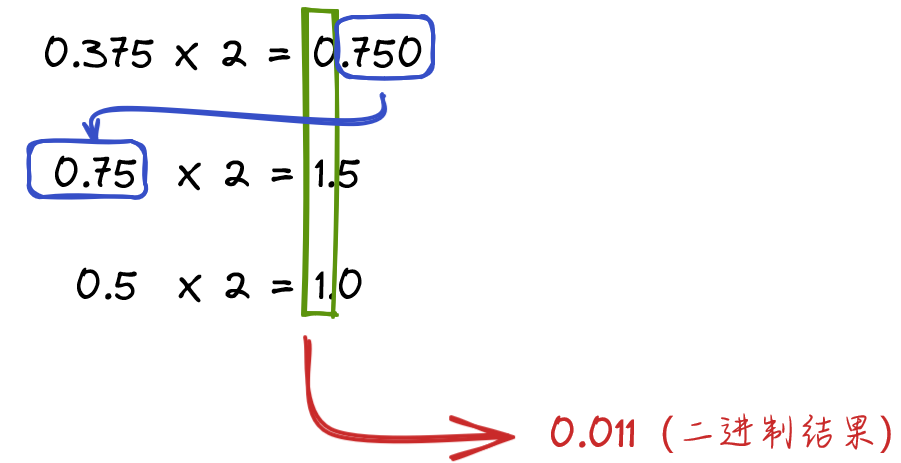
    另外，二进制0.011转十进制小数的方法，如下图

 （2）规格化编码

      同样以0.375为例，按R32.23格式将其编码：

• 移动二进制小数点，使最高有效数字为1

          0.011右移2位变成 1.1。相反的，1.1需左移2位变成0.011，所以

          frac = 0.1 （1.1 隐藏整数1）

          M = exp - 127 = -2，求得 exp = 125

          s = 0

• 转成规格化编码格式为

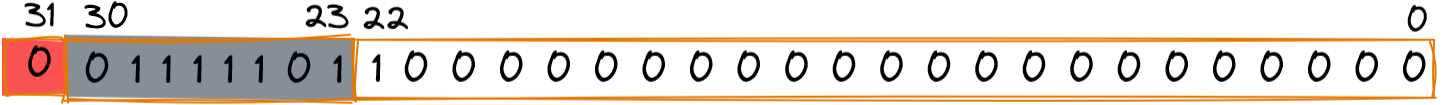
  十六进制即为0x3EC00000。

3. 浮点数舍入

    在浮点运算中，当运算结果超出表示范围时会对数值进行舍入，IEEE浮点格式定义了四种不同的舍入方式，默认为“向最接近的值舍入”，也叫“向偶数舍入”，类似十进制中的“四舍五入法”，但只在“五入”后最低有效位为偶数才会“入”，否则就舍弃。

举例1：

   预丢弃的10最高位为1，应该向bit0 进位，但若进位后bit0 = 1，不符合最低有效数为偶数的要求，所以直接丢弃超出的 10.

举例2：

   若向bit0进位后 bit1 ~ bit0 = 10，此时bit0为偶数0，所以可以向bit0进位。

   注意， 在从float或者double强转int时，会采用另一种舍入方式（向零舍入），即舍弃小数部分，只保留整数部分。