w9_02

# 求二叉树中节点间的宽度

## 题目描述

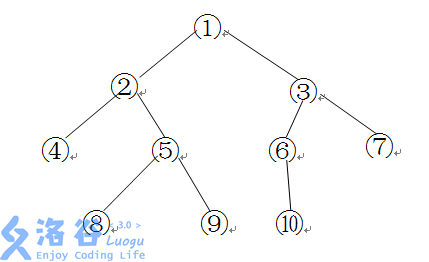
如下图所示的一棵二叉树的深度、宽度及结点间距离分别为：

深度：4 宽度：4（同一层最多结点个数）

结点间距离： ⑧→⑥为8 (3×2+2=8)

⑥→⑦为3 （1×2+1=3）

注：结点间距离的定义：由结点向根方向（上行方向）时的边数×2，

与由根向叶结点方向（下行方向）时的边数之和。


## 输入格式

输入文件第一行为一个整数n(1≤n≤100)，表示二叉树结点个数。接下来的n-1行，表示从结点x到结点y（约定根结点为1），最后一行两个整数u、v，表示求从结点u到结点v的距离。

## 输出格式

三个数，每个数占一行，依次表示给定二叉树的深度、宽度及结点u到结点v间距离。

## 样例 #1

### 样例输入 #1

```
10
1 2
1 3
2 4
2 5
3 6
3 7
5 8
5 9
6 10
8 6
```

### 样例输出 #1

```
4
4
8
```

对于深度：在输入x,y的时候如果x是y的根，我们的deep加一，直到输入循环结束，输出我们的deep

对于宽度：我们记录在每个深度处的节点个数，也就是我们的宽度，最后对宽度进行排序，输出我们最大的宽度即可

对于两个节点之间的距离：我们要寻找到两个节点的最近公共祖先，我们对所有的节点都初始标记为零然后由一个节点开始往上开始搜索，搜索过的节点标记为1，一直到最后的根节点，我们探索一步就把计数器加一，（注意这个计数器要*2），右节点也是往上搜索，直到搜索到的节点是1，此时被搜索到的节点就是最近公共祖先，同样每搜索一步计数器加一，最后两个计数器相加就是距离。

具体代码如下：

#include<bits/stdc++.h>
using namespace std;
struct node{
int father; //爸爸
int left; //左儿子
int right; //右儿子
int deep; //深度
int data; //记录节点走过没
}a[10001];
int sum[101];
int lca(int x,int y){ //最最重要！！！求最近公共祖先
a[x].data=1; //把x的节点记录已走过
while(a[x].father!=0){ //遍历至根节点
x=a[x].father; //更新遍历爸爸
a[x].data=1; //记录已走过
}
while(a[y].data!=1){ //遍历至x节点已走过的节点，找到最近公共祖先
y=a[y].father;
}
return y;
}
int main(){
int n,x,y,s,t,maxx=1;
cin>>n;
a[1].deep=1; //根节点的深度为1
a[1].father=0; //根节点没有爸爸
for(int i=1;i<n;i++){
cin>>x>>y;
if(a[x].left==0) //这个节点是否有左儿子
a[x].left=y; //变成左儿子
else //变成右儿子
a[x].right=y;
a[y].father=x;
a[y].deep=a[x].deep+1; //更新深度
if(a[y].deep>maxx) //求出最大深度，第一个问题完成
maxx=a[y].deep;
}
cin>>s>>t;
int f=lca(s,t),num=0,num1=0;
while(s!=f){ //记录s到最近公共祖先有多少条边
s=a[s].father;
num++;
}
num*=2; //结点间距离的定义：由结点向根方向（上行方向）时的边数×2，
while(t!=f){ //记录t到最近公共祖先有多少条边
t=a[t].father;
num1++;
}
for(int i=1;i<=n;i++) //把每一个深度有多少个节点记录
sum[a[i].deep]++;
sort(sum+1,sum+1+100);
cout<<maxx<<endl<<sum[100]<<endl<<num+num1; //sum[100]是最大的宽度节点个数
return 0;
}