Understanding Convolutions

从信号分析来理解卷积公式

1-Def

卷积公式同加法乘法一样，都是一种运算，他在特定的运算中会基于计算很大的便利，其次它也拥有很多性质，但是透过简单的定义式我们却很难直观的感受到其背后的物理意义，这对于理解来说是困难的，因此我们尝试通过信号处理方法来解释一下卷积公式所蕴含的物理意义，并通过一个实例来体现卷积公式是如何简化我们的运算的。

若我们定义两个函数\(f、g\)的卷积运算\(f*g(n)\)如下，它具有两种等价的形式：

\[(f*g)(n)::=\begin{cases} \int_{-\infty}^\infty f(\tau)g(n-\tau)d\tau&连续形式\\ \\ \sum f(\tau)g(n-\tau),\tau\in\R&离散形式 \end{cases} \]

注意到：\(\tau+(n+\tau)=n\rightrightarrows x+y=n\)是一条垂直于\(y=x\)的直线，而随着\(n\)的改变，这条直线会沿着\(y\)轴方向平移，如图：

而当我们考察函数\(\int f(\tau)g(n-\tau)d\tau\),事实上通过遍历\(\tau\in(-\infty,\infty)\)，我们可以得到所有\(x+y=n\)的点，相当于将坐标系以\(y=-x\)方向，“卷”起来，最终会得到一个一维的长度为\(n\)的张量，在连续情况下，叠加指的是对两个函数的乘积求积分，上面每一点的值代表将在\(x+y=n\)直线上的所有\(f(x)g(y)\)的积相加，在离散情况下就是加权求和，为简单起见就统一称为叠加。

那么，整体看来是这么个过程：

翻转\(\to\)滑动\(\to\)叠加\(\to\)滑动\(\to\cdots\to\)滑动\(\to\)叠加\(\to\cdots.\)

多次滑动得到的一系列叠加值，构成了卷积函数。

对卷积的意义的理解：

1. 从“积”的过程可以看到，我们得到的叠加值，是个全局的概念。以信号分析为例，卷积的结果是不仅跟当前时刻输入信号的响应值有关，也跟过去所有时刻输入信号的响应都有关系，考虑了对过去的所有输入的效果的累积。在图像处理的中，卷积处理的结果，其实就是把每个像素周边的，甚至是整个图像的像素都考虑进来，对当前像素进行某种加权处理。所以说，“积”是全局概念，或者说是一种“混合”，把两个函数在时间或者空间上进行混合。

2. 那为什么要进行“卷”？直接相乘不好吗？我的理解，进行“卷”（翻转）的目的其实是施加一种约束，它指定了在“积”的时候以什么为参照。在信号分析的场景，它指定了在哪个特定时间点的前后进行“积”，在空间分析的场景，它指定了在哪个位置的周边进行累积处理。

2-Application

1.丢骰子

有两枚骰子，把它们都抛出去，两枚骰子点数加起来为4的概率是多少?

设\(f(X=x_i)\)为骰子投出\(\{x_i|i\in(1,6)\sub\N\}\)的概率，同理可设\(g(Y)\).则经过分析可知，当两个骰子点数为 4 时，可能存在三种情况：

\[f(1)g(3)+f(2)g(2)+f(3)g(1)=(f*g)(4)=\sum_{i=1}^3f(\tau)g(4-\tau) \]

首先，因为两个骰子的点数和是4，为了满足这个约束条件，我们还是把函数 g 翻转一下，然后阴影区域上下对应的数相乘，然后累加，相当于求自变量为4的卷积值，如下所示：

				\(\downarrow\)	\(\downarrow\)	\(\downarrow\)
f:				1	2	3	4	5	6
g:	6	5	4	3	2	1
				\(\uparrow\)	\(\uparrow\)	\(\uparrow\)

进一步，如此翻转以后，可以方便地进行推广去求两个骰子点数和为 n 时的概率，为\(f\) 和$ g$的卷积 \(f*g(n)\).

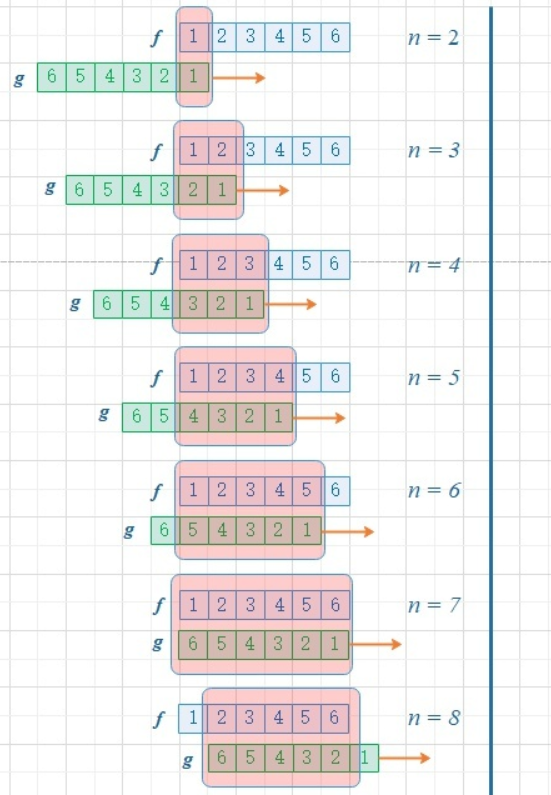
由上图可以看到，函数 g 的滑动，带来的是点数和的增大。这个例子中对f和g的约束条件就是点数和，它也是卷积函数的自变量。有兴趣还可以算算，如果骰子的每个点数出现的概率是均等的，那么两个骰子的点数和n=7的时候，概率最大。

2.信号处理

如下图所示，输入信号是 f(t) ，是随时间变化的。系统响应函数是 g(t) ，图中的响应函数是随时间指数下降的，它的物理意义是说：如果在 t=0 的时刻有一个输入，那么随着时间的流逝，这个输入将不断衰减。换言之，到了 t=T时刻，原来在 t=0 时刻的输入f(0)的值将衰减为f(0)g(T)。

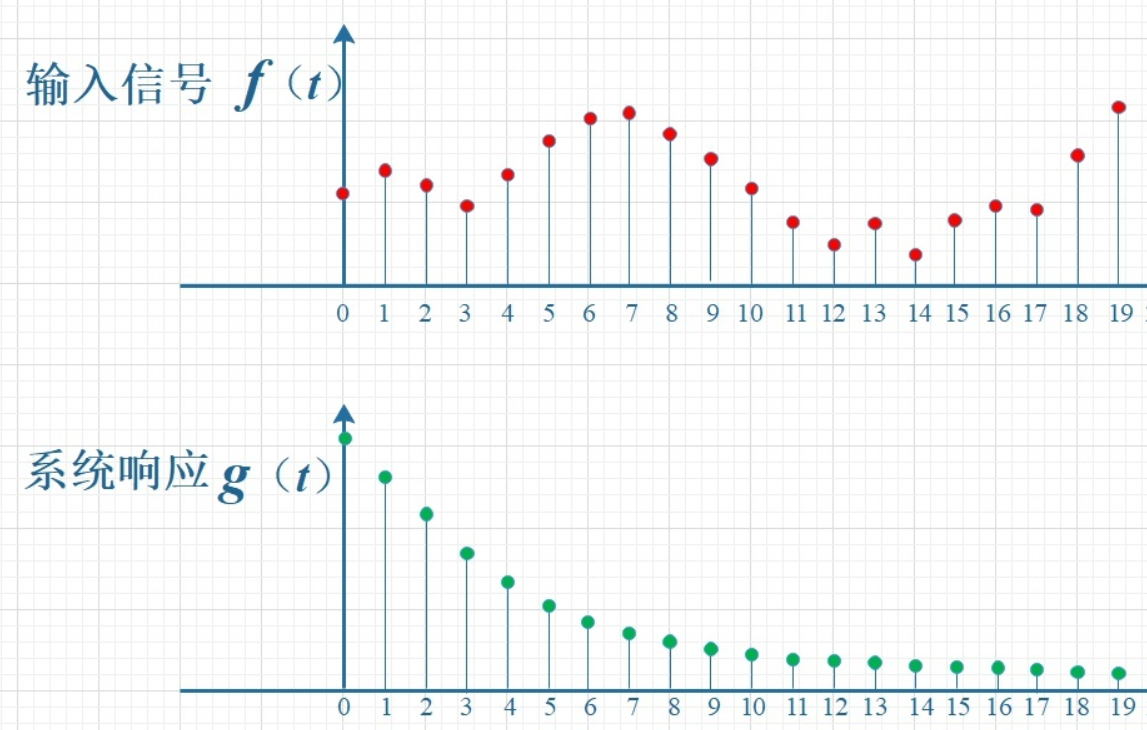
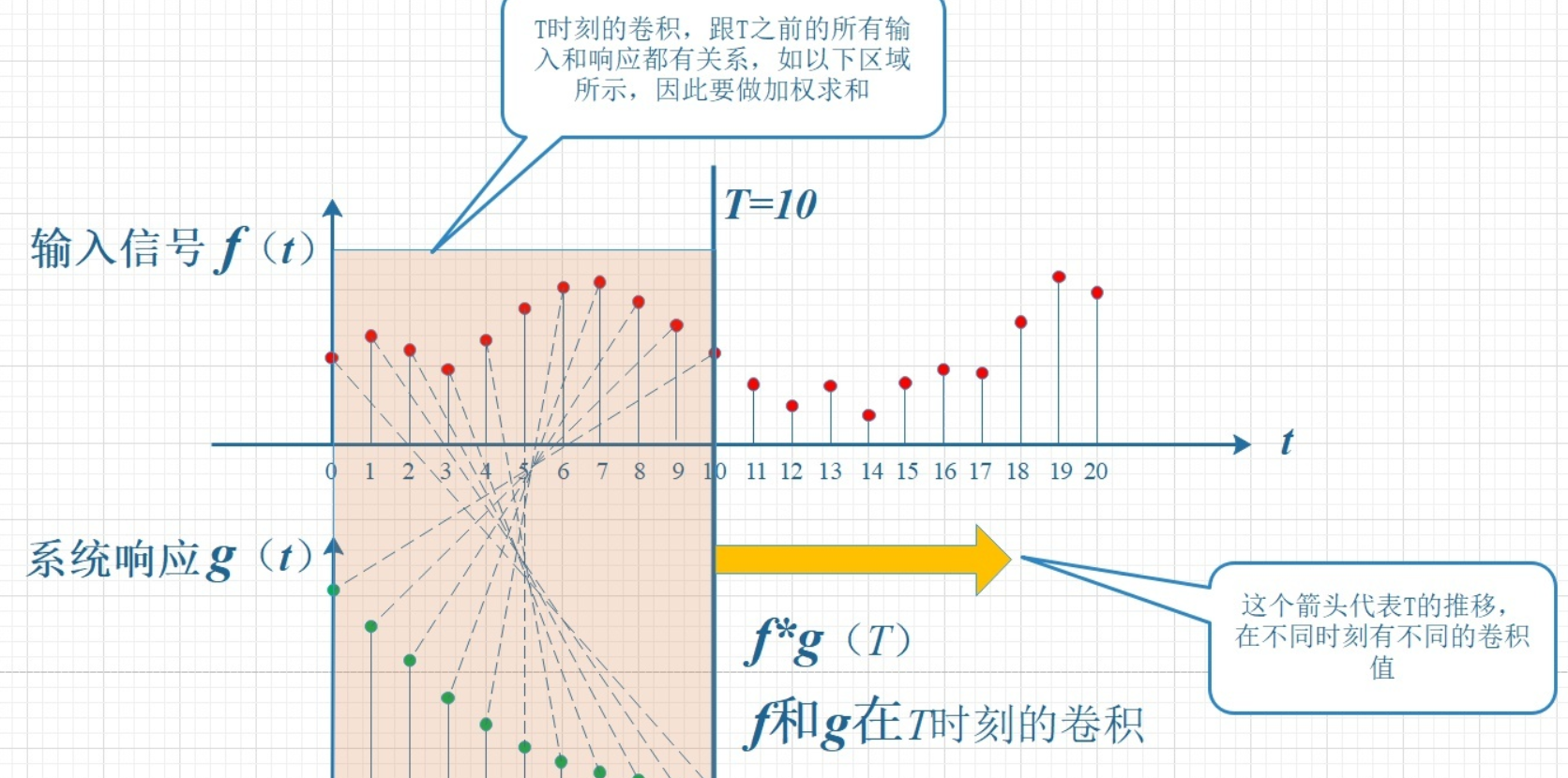
考虑到信号是连续输入的，也就是说，每个时刻都有新的信号进来，所以，最终输出的是所有之前输入信号的累积效果。如下图所示，在T=10时刻，输出结果跟图中带标记的区域整体有关。其中，f(10)因为是刚输入的，所以其输出结果应该是f(10)g(0)，而时刻t=9的输入f(9)，只经过了1个时间单位的衰减，所以产生的输出应该是 f(9)g(1)，如此类推，即图中虚线所描述的关系。这些对应点相乘然后累加，就是T=10时刻的输出信号值，这个结果也是f和g两个函数在T=10时刻的卷积值。

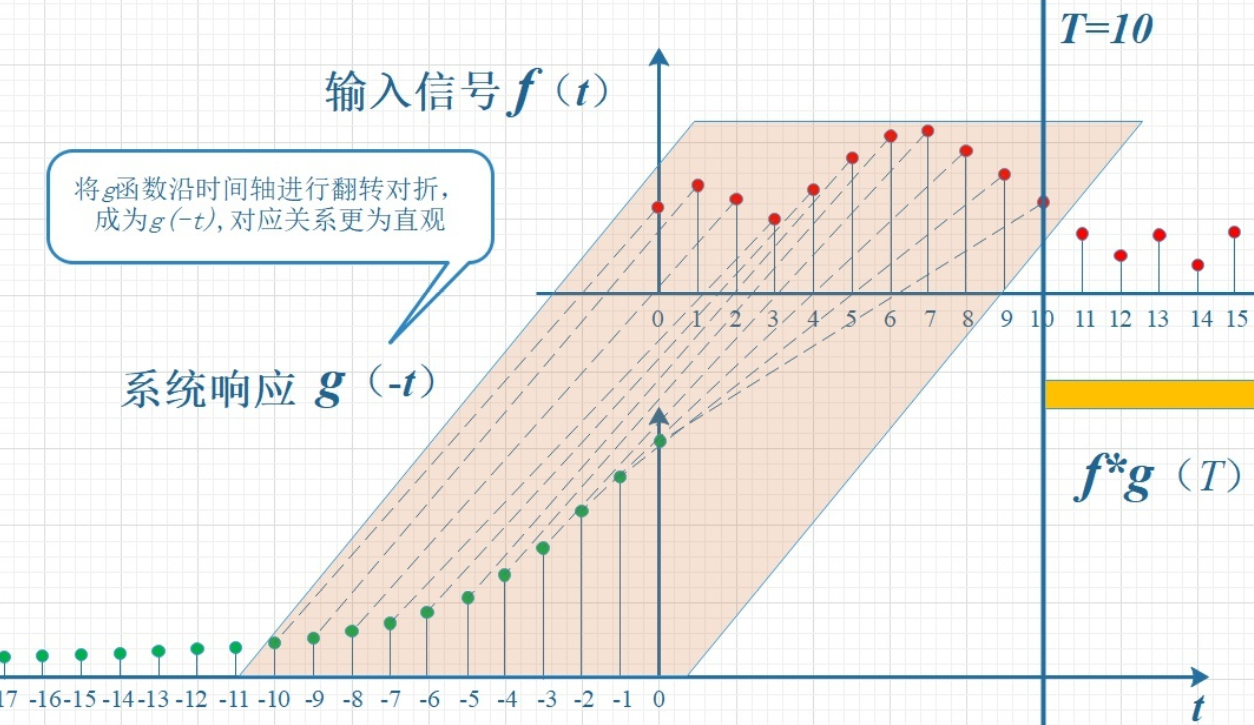
显然，上面的对应关系看上去比较难看，是拧着的，所以，我们把g函数对折一下，变成了g(-t)，这样就好看一些了。看到了吗？这就是为什么卷积要“卷”，要翻转的原因，这是从它的物理意义中给出的。

上图虽然没有拧着，已经顺过来了，但看上去还有点错位，所以再进一步平移T个单位，就是下图。它就是本文开始给出的卷积定义的一种图形的表述：

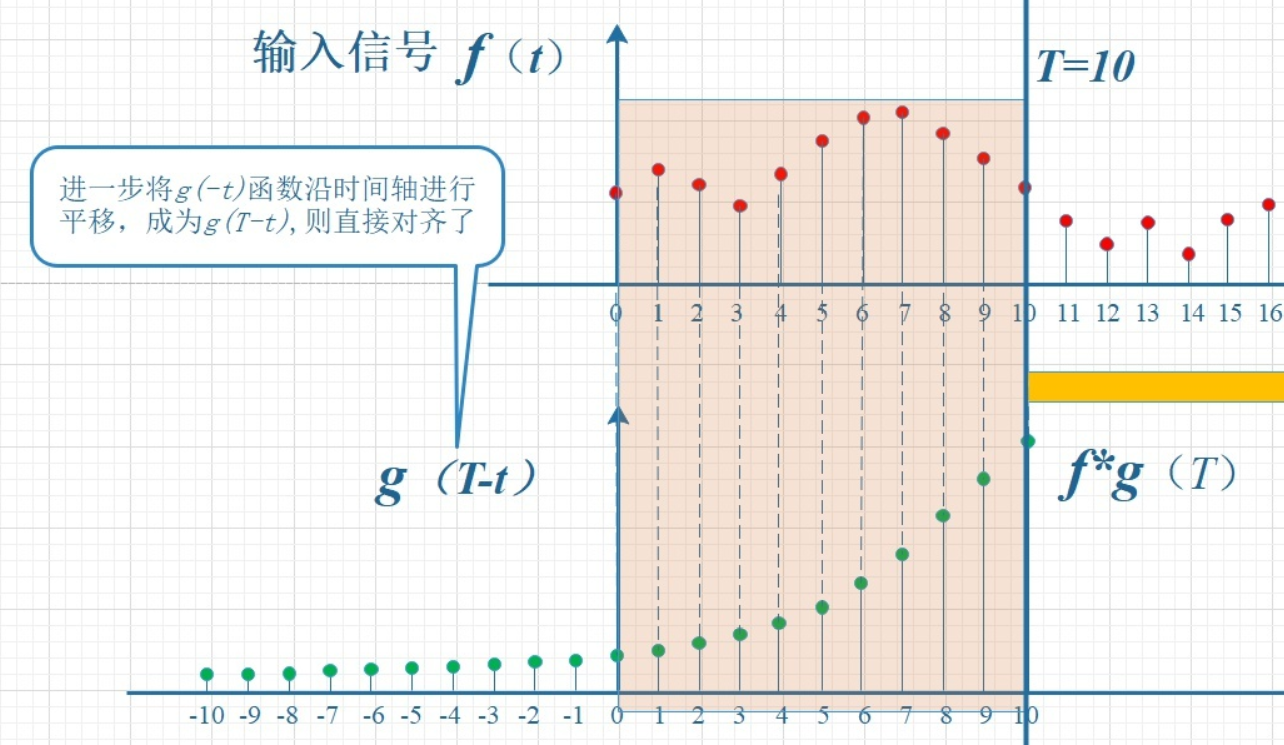
所以，在以上计算T时刻的卷积时，要维持的约束就是： t+ (T-t) = T 。

3-features

代数性值

• (交换律)：\(f_1(x)*f_2(x)=f_2(x)*f_1(x)\)
• (分配律)：\(f_1(x)*(f_2(x)+f_3(x))=f_1(x)*f_2(x)+f_1(x)*f_3(x)\)
• (结合律)：\(f_1(x)*(f_2(x)*f_3(x))=(f_1(x)*f_2(x))*f_3(x)\)

微分性质

若\(g(x)=f(x)*h(x)\)，则\(g'(x)=f(x)*h'(x)=f'(x)*h(x)\)$。

因为

\[g(x)=f(x)*h(x)=\int_{-\infty}^\infty f(\tau)g(x-\tau)d\tau \]

则

\[\begin{align} \frac{dg(x)}{dx}=&\frac{d\int_{-\infty}^\infty f(\tau)g(x-\tau)d\tau}{dx}\\ =&\int_{-\infty}^\infty f(\tau)\,\frac{dg(x-\tau)}{dx}d\tau\\ =&\int_{-\infty}^\infty f(\tau)g'(x-\tau)d\tau\\ =&f(x)g'(x) \end{align} \]

推广：

• \(g(x)=f'(x)*h^{(-1)}(x)\);
• \(g^{(n)}(x)=f(x)*h^{(n)}(x)=f^{(n)}(x)*h(x)\);
• \(g^{(n-m)}(x)=f^{(-m)}(x)*h^{(n)}(x)=f^{(n)}(x)*h^{(-m)}(x)\)