自然语言处理——词的表示

1、词向量（Word Vectors）

英语中大约有13亿个符号，从Feline（猫科动物）到cat（猫），hotel（旅馆）到motel（汽车旅馆），很明显它们之间是有关联的。我们需要将单词一一编码到向量中，一个向量表示了词空间中的一个点。

最简单的一种词向量就是one-hot向量：将每个词都表示为一个$\mathbb{R}^{\left | V \right | \times 1}$的向量，改词在词表中索引的位置是1，其他位置都是0。$\left | V \right |$是词表的大小。one-hot词向量形式如下：

\begin{align*}
w^{aardvark} = \begin{bmatrix}1\\ 0\\ 0\\ \vdots \\ 0 \end{bmatrix},
w^{a} = \begin{bmatrix}0\\ 1\\ 0\\ \vdots \\ 0 \end{bmatrix},
w^{at} = \begin{bmatrix}0\\ 0\\ 1\\ \vdots \\ 0 \end{bmatrix},
\cdots ,
w^{zebra} = \begin{bmatrix}0\\ 0\\ 0\\ \vdots \\ 1 \end{bmatrix}
\end{align*}

虽然我们成功地将每个词都表示为了不同的实体，但这一表示方式并不能提供词之间相似性的概念，例如：

\begin{align*}
(w^{hotel})^Tw^{motel} = (w^{hotel})^Tw^{cat} = 0
\end{align*}

我们需要找到一个空间，该空间维度远小于$\mathbb{R}^{\left | V \right | \times 1}$，并且该空间中的词向量，可以体现出词之间的相似度。

2、基于SVD（奇异值分解）的方法

为了找到词嵌入（word embeddings，可以简单的理解为与词向量等价），可以首先遍历巨大的语料库，统计两个词之间某种形式的共现次数，并将统计值保存在一个矩阵$X$中。然后应用奇异值分解：$X = USV^T$。我们使用$U$中的每一行作为每个词的词嵌入。下面将讨论$X$的一些选择方式。

2.1 词-文档矩阵（Word-Document Matrix）

作为第一次尝试，我们首先大胆地猜想，经常出现在同一文档中的词是有关联的。比如，"banks"、"bonds"、"stocks"、"money"等等，很可能会共同出现。但是"banks"、"octopus"、"banana"、"hockey"并不能经常共现。基于这一事实创建一个词-文档矩阵$X$，方法如下：遍历数以亿计的文档，每当第$i$个词出现在第$j$个文档中，就对矩阵中元素$X_{i,j}$加一。最终得到的是一个庞大的$\mathbb{R}^{\left | V \right | \times M}$矩阵，并且还会随着文档数量（$M$）缩放比例。该方案显然很不理想。

2.2 基于窗口的共现矩阵（Window based Co-occurrence Matrix）

这个方法不再考虑文档的数量，统计两个词在给定窗口中的共现次数。例如，语料是下面的三句话，窗口大小是1：

1. I enjoy flying.
2. I like NLP.
3. I like deep learning.

共现矩阵为：

2.3 对共现矩阵应用SVD

对$X$应用SVD：

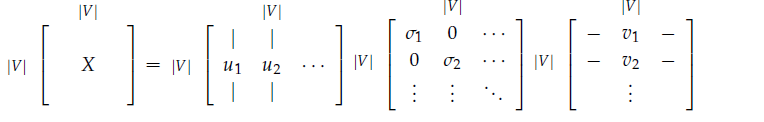
中间的矩阵除了对角线，其他位置都是0。对角线上的元素$\sigma_i$称为奇异值。我们可以从矩阵U中选取前$k$列，作为词向量。而这前$k$列所能保存的原数据的方差（variance）比例为：

\begin{align*}
\frac{\sum_{i=1}^{k} \left | \sigma_i \right |}{\sum_{i=1}^{\left | v \right |} \left | \sigma_i \right |}
\end{align*}

通过选取前$k$列奇异向量进行降维：

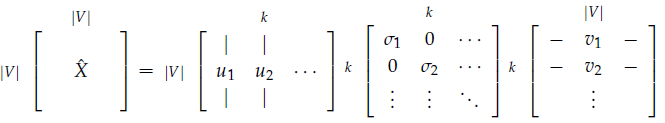
用这种方式生成的词向量保留了足够多的语法和语义信息，但也还是存在一些问题：

矩阵维度经常变动，比如新词频繁加入。
由于绝大部分词并不会共现，造成矩阵过于稀疏。
矩阵维度一般很高，大约$10^6 \times 10^6$。
并且难以合并新词或新的文档。对于一个$m \times n$矩阵，训练时的计算复杂度是$O(mn^2)$
由于词频的极度不平衡，需要对矩阵$X$应用一些黑科技。

上述问题的一些解决方案：

忽略the、he、has等虚词。
应用一个斜坡窗口（ramp window，也就是说，不再对窗口内的所有词一视同仁）——比如，根据距离当前词的距离，对共现次数赋予相应的权重。
使用皮尔逊相关系数（Pearson correlation coefficient），取代直接计数。

看了下一小节我们就会发现，基于迭代的方法可以使用更优雅的方式解决上述问题。

3 基于迭代的方法——Word2vec

与之前计算和存储巨大数据集的全局信息不同，现在我们用反向传播训练一个模型，预测一个词在给定上下文存在的概率，该模型的参数就是词向量。下面介绍一个简单的、较新的、基于概率的模型——word2vec：

两个算法：continuous bag-of-words (CBOW)和skip-gram。CBOW是给定上下文环境时，预测该环境中间的那个中心词。Skip-gram正好相反，预测一个中心词上下文环境的分布。
两个训练方法：负采样（negative sampling）和分层softmax。

word2vec概况：https://myndbook.com/view/4900

3.1 语法模型（一元、二元）

首先我们来定义一个模型，该模型可以给一个符号序列分配概率。以下面的句子为例：

"The cat jumped over the puddle."

一个好的语言模型，会给上面的句子分配一个较高的概率。因为这个句子在语法和语义上都是正确的。数学上，这$n$个词的概率可表示为：

\begin{align*}
p(w_1, w_2, \cdots, w_n)
\end{align*}

一元语法模型就是假设每个词都是独立的，这会大大降低联合概率的复杂性：

\begin{align*}
p(w_1, w_2, \cdots, w_n) = \prod_{i=1}^{n}P(w_i)
\end{align*}

但这一模型是很荒唐的。因为我们知道，后词对它前面序列的依赖性是很高的。这也可能会使得错误的句子得到一个较高的概率。所有这就有了二元语法模型，当前词只依赖于它前面的一个词：

\begin{align*}
p(w_1, w_2, \cdots, w_n) = \prod_{i=2}^{n}P(w_i|w_{i-1})
\end{align*}

虽然这一模型也很幼稚，但它的效果还可以。

现在我们已经知道，一个符号序列是可以有概率的。下面将介绍可以学习这些概率的模型。

3.2 连续词袋模型（Continuous Bag of Words Model，CBOW）

把{"The", "cat", ’over", "the’, "puddle"}看作是上下文环境，来预测中间的单词"jumped"，这就是CBOW模型。这是一个简单的神经网络，如下所示：

图1 CBOW工作原理

我们定义输入层到隐层的权重矩阵为$\mathcal{V} \in \mathbb{R}^{n \times \left | V \right |} $（也就是上图中的$W_{V \times N}$），隐层到输出层的权重矩阵为$\mathcal{U} \in \mathbb{R}^{\left | V \right | \times n}$（也就是上图中的$W'_{N \times V}$）。其中，$n$是隐层神经元个数，也是词嵌入空间的维度。$\mathcal{V}$是输入词矩阵，当一个词$w_i$作为输入进入模型时，$\mathcal{V}$的第$i$列就是该词的嵌入向量。这一$n \times1$向量记为$v_i$。类似的，$\mathcal{U}$是输出词矩阵，当一个词$w_j$是该模型的输出时，$\mathcal{U}$的第$j$行就是该词的嵌入向量。这一$1 \times n$矩阵记为$u_j$。所以，在模型中，一个词是对应两个词向量的。

用反向传播训练这一神经网络：

假设窗口为$m$，输入数据就是上下文环境中$2m$个词的one-hot向量：$x^{(c-m)},\cdots ,x^{(c-1)},x^{(c+1)},\cdots x^{(c+m)} \in \mathbb{R}^{\left | V \right |}$
获取上下文环境的嵌入词向量：$v_{c-m} = \mathcal{V}x^{(c-m)},\cdots ,v_{c+m} = \mathcal{V}x^{(c+m)} \in \mathbb{R}^n$
计算这次嵌入词向量的均值：$\hat{v} = \frac{v_{c-m} + \cdots + v_{c+m}}{2m}$
生成一个分值向量$z = \mathcal{U}\hat{v} \in \mathbb{R}^{\left | V \right |}$。由于相似向量的内积较大，这会使得相似词的向量越来越相似，以便得到较高的分值
应用softmax激活函数，将分值转换为概率$\hat{y} = \mbox{softmax}(z) \in \mathbb{R}^{\left | V \right |}$
神经网络的目标值就是中心词"jumped"的one-hot向量，记为$y$。定义损失函数为交叉熵损失，反向传播进行训练。

假设$c$是目标值one-hot向量为1的位置的索引，损失函数：

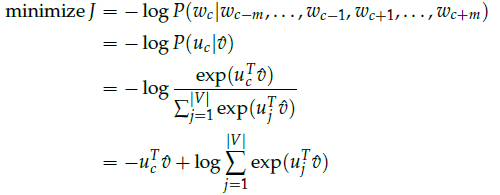
3.3 Skip-Gram模型

这次给定中心词"jumped"，然后预测它周围的词"The", "cat", "over", "the", "puddle"。这也是一个神经网络，如下所示：

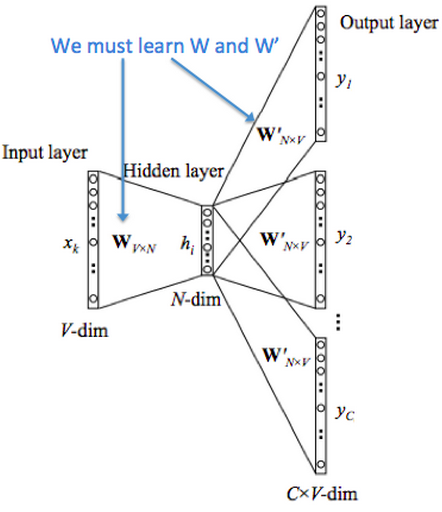
图2 Skip-Gram工作原理

定义同样的$\mathcal{V} \in \mathbb{R}^{n \times \left | V \right |} $和$\mathcal{U} \in \mathbb{R}^{\left | V \right | \times n}$，训练这一神经网络

输入向量$x \in \mathbb{R}^{\left | V \right |}$是中心词的one-hot向量。
计算中心词的嵌入词向量$v_c = \mathcal{V}x \in \mathbb{R}^n$
计算分值向量$z = \mathcal{U}v_c$
使用softmax激活函数，将分值转换为概率$\hat{y} = \mbox{softmax}(z) \in \mathbb{R}^{\left | V \right |}$
目标值是中心词周围那些词的one-hot向量，记为$y^{(c-m)},\cdots ,y^{(c-1)},y^{(c+1)},\cdots ,y^{(c+m)}$。

定义损失函数：

\begin{align*}
J = -logP(w_{c-m},\cdots ,w_{c-1},w_{c+1},\cdots ,c_{c+m}|w_c)
\end{align*}

为了简化模型，我们假设这些条件概率相互独立（朴素贝叶斯假设），从而有：

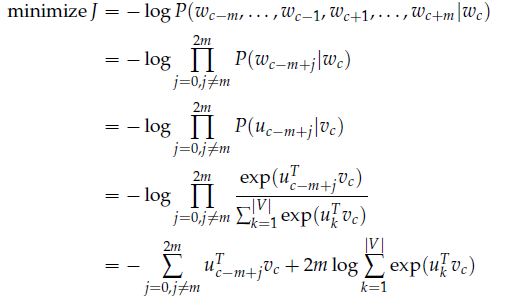
此外，

\begin{align*}
J &= -log\prod_{j=0,j\neq m}^{2m}P(w_{c-m+j}|w_c) \\
&= -log\prod_{j=0,j\neq m}^{2m}P(u_{c-m+j}|v_c) \\
&= -\sum_{j=0,j\neq m}^{2m}logP(u_{c-m+j}|v_c) \\
&= \sum_{j=0,j\neq m}^{2m}H(\hat{y},y_{c-m+j})
\end{align*}

其中，$H(\hat{y},y_{c-m+j})$是交叉熵。

3.4 Negative Sampling

我们再回头观察一下损失函数，对整个$\left | V \right |$求和，计算量巨大。每一次更新或者评估损失函数，都会有$O(\left | V \right |)$的时间复杂度。我们必须减少这一计算量。
在训练时的每一步，与遍历整个词汇表不同，这次只需要抽样部分反面例子（negative examples）。我们从一个噪声分布（$P_n(w)$，noise distribution）抽样，其概率分布与词汇表的词频相对应。

虽然negative sampling基于Skip-Gram模型，事实上前者是在优化一个不同的目标函数。考虑一个词（word）和上下文环境（context）的组合$(w,c)$。将$(w,c)$在语料中存在的概率记为$P(D=1|w,c)$，在语料中不存在的概率记为$P(D=0|w,c)$。首先使用sigmoid函数对$P(D=1|w,c)$建模：

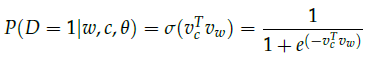
然后，应用极大似然估计，创建新的目标函数，使得$P(D=1|w,c)$最大，$P(D=0|w,c)$最小（此时模型的参数是$\theta$，在外面之前的例子中是$\mathcal{V}$和$\mathcal{U}$）：

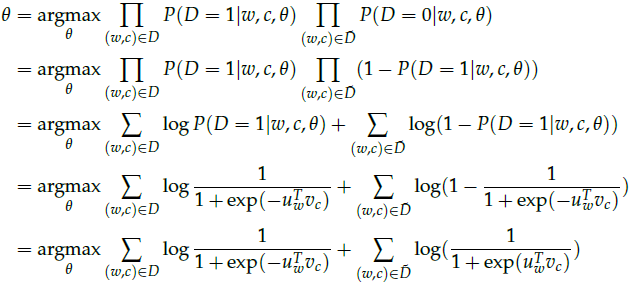
最大似然和最小负log似然是等价的：

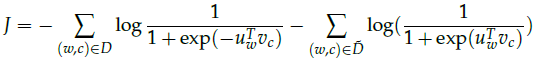
其中，$\widetilde{D}$是错误的、反面的语料。也就是说，类似"stock boil fish is toy"不通顺的句子。可以从词库中随机抽样，生成这种错误的句子。

对于skip-gram模型，给出中心词$c$并观察它窗口内的单词$c-m+j$时的损失函数更新为：

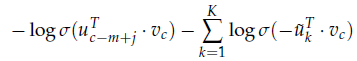
对于CBOW模型，给出上下文环境$\hat{v} = \frac{v_{c-m} + \cdots + v_{c+m}}{2m}$并观察到中心词$u_c$时的损失函数更新为：

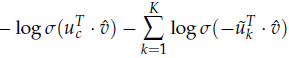
在上面的公式中，$\{ \widetilde{u_k}|k=1,\cdots ,K \}$是从$P_n(w)$抽样而来的。为了达到最佳逼近效果，采用了一元语法模型，并对词频取3/4次幂。下面一个例子，说明了为什么是3/4：

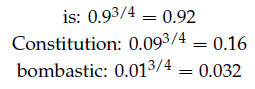
"Bombastic"被抽样的概率，增加到原来的三倍，而"is"几乎不变。

3.5 分层Softmax

Mikolov等人表明，分层softmax的效率要远高于普通的softmax。在实践中，分层softmax更擅长于处理不常见的词汇，而negative sampling更擅长处理常见词汇以及生产更低维度的向量。

分层softmax使用一棵二叉树来表示词表中的所有词汇。每个叶节点都是一个词，并且从根节点到叶节点的路径是唯一的。该模型并不会输出词汇的向量表示，不过图中的每一个节点（除了根节点和叶子节点）都对应一个向量，这些向量是模型需要学习的参数。

现在需要引入一些概念。用$L(w)$表示从根节点到叶节点$w$的节点数。例如，在图3中，$L(w_2) = 3$。记$n(w,i)$是路径上的第$i$个节点，相应的向量为$v_{n(w,i)}$。因此$n(w,1)$是根节点，$n(w,L(w))$是$w$的父节点。对于每个中间节点$n$，我们任意选择它的一个子节点并称之为$ch(n)$（这是在模型训练开始之前就选好的。每个中间节点都有两个子节点，可以任意选择。在本文中，每次都选左侧子节点）。

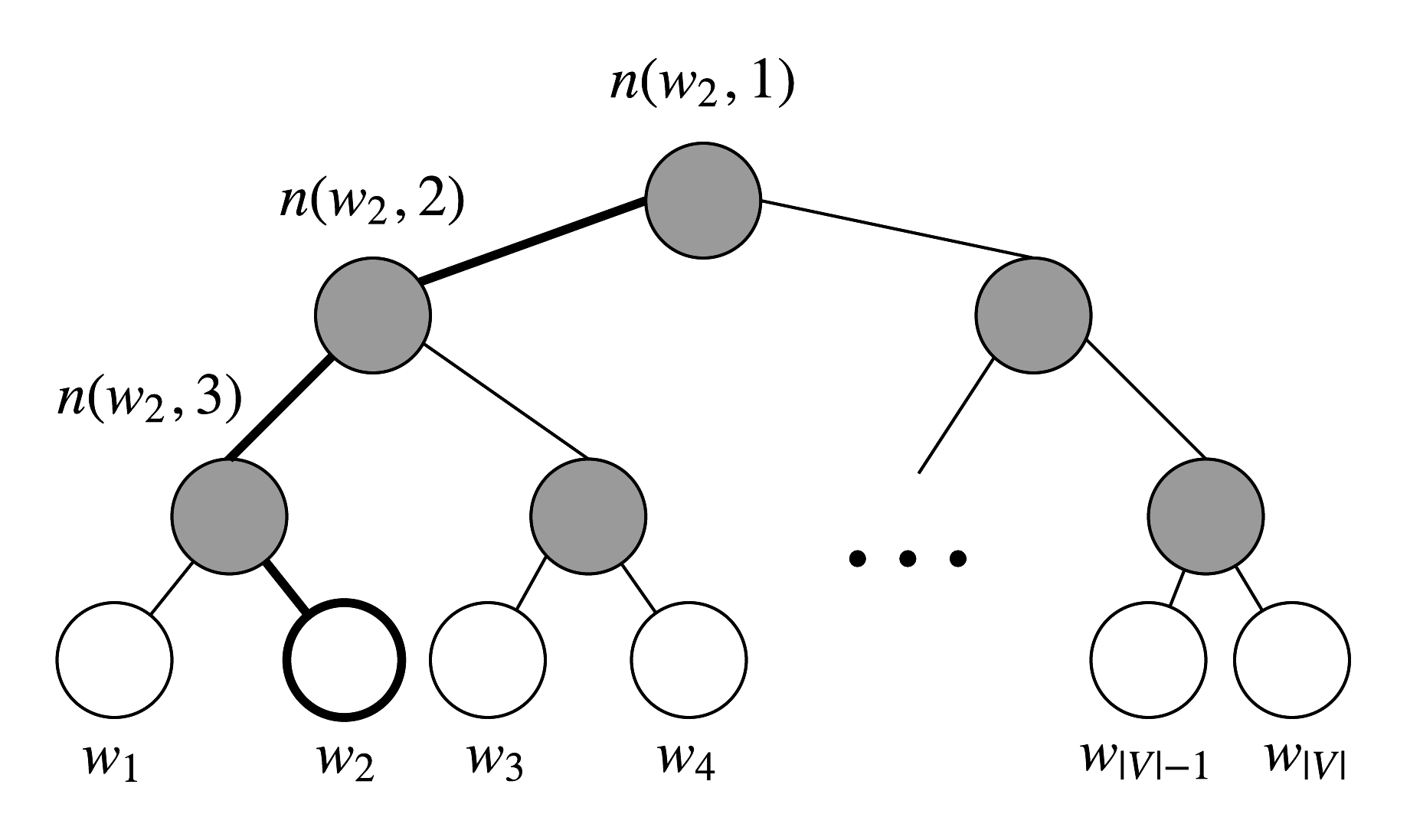
图3 分层Softmax的二叉树

然后计算如下形式的概率：

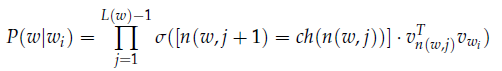
其中，

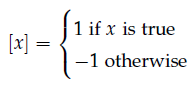
此外，$\sigma(\cdot)$是sigmoid函数。

上面的公式信息量比较大，我们来详细地解释一下：

公式的最右侧是在计算向量内积。$v_{n(w,j)}$的长度是在变动的，所以每次$v_{w_i}$都截取相应的位数。我们假设$ch(n)$每次都是左侧的子节点。所以单词$w$真实的路径是向左时，$[ n(w,j+1) = ch(n(w,j))]$返回1，否则返回-1。

此外，$[ n(w,j+1) = ch(n(w,j))]$可以起到标准化（normalization）的作用。对于任一节点，走向左节点的概率和走向右节点的概率之和都应该为1（因为就两个子节点，不是向左就是向右）。对于任意的$v_n^Tv_{w_i}$，下面等式始终都是成立的：

\begin{align*}
\sigma(v_n^Tv_{w_i}) + \sigma(-v_n^Tv_{w_i}) = 1
\end{align*}

这其实也很好证明。sigmoid函数的定义：

\begin{align*}
\sigma(x) = \frac{1}{1 + e^{-x}}
\end{align*}

从而可得：

\begin{align*}
\sigma(x) + \sigma(-x) &= \frac{1}{1 + e^{-x}} + \frac{1}{1 + e^{x}} \\
&= \frac{1 \cdot e^x}{(1 + e^{-x}) \cdot e^x} + \frac{1}{1 + e^{x}} \\
&= \frac{e^x}{e^x + 1} + \frac{1}{1 + e^{x}} \\
&= 1
\end{align*}

这也保证了$\sum_{w=1}^{\left | V \right |} P(w|w_i) = 1$是成立的。

为了训练这一模型，我们的损失函数依然是负log loss（与交叉熵一样）：$-logP(w|w_i)$。

本文翻译自CS224n课程的官方笔记1，对应该课程的第1、2节。

posted on 2018-06-02 14:17 royhoo 阅读(3402) 评论(0) 编辑收藏举报

会员力量，点亮园子希望

刷新页面返回顶部

royhoo