PAT (Top Level) Practice 1002 Business 题解

题目描述：

输入输出样例：

 

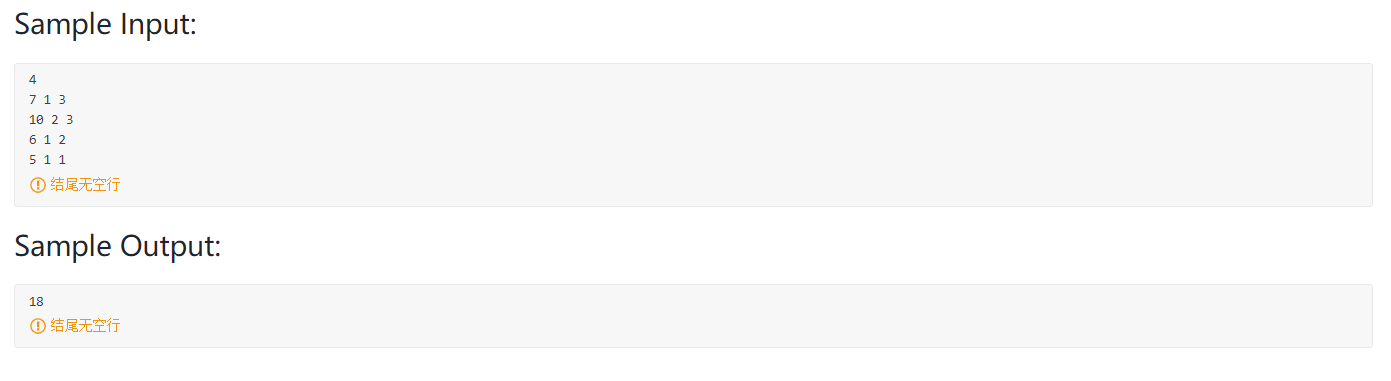
解题思路：

刚开始看到题目的时候，我还以为是一道正儿八经的线性DP题目

后来定睛一看，这分明就是01背包的魔改版嘛

最大的DDL日期是背包容量，每个项目的得分是价值，然后我们就可以开始愉快的写01背包了~

需要注意的是，本题的递推方程和01背包有些许不同

因为在选出的项目列表里，前后两个项目的时间不一定衔接，即上一个项目的DDL不一定就是下一个项目的开始时间，于是乎不能照抄01背包模板

所以我们的递推方程应该改为：

dp[i][j]=max(dp[i-1][j],dp[i-1][min(j,D[i])-L[i]]+P[i])//D是DDL，L是每个项目需要时间长度，P是每个项目得分

我们也可以用滚动数组优化掉第一维，把递推方程简化为：

dp[j]=max(dp[j],dp[min(j,D[i])-L[i]]+P[i])

同时在输入前应当对输入数据进行预处理，将结束时间早的放在前面，即可将改问题转为01背包问题

PS:每一个项目只需要在DDL前完成即可，我一开始还以为每个项目固定了开始和结束时间QAQ

代码：

 

#include <iostream>
#include <cstdio>
#include <algorithm>
using namespace std;
int n,dp[1000005];
struct project{
    int p,l,d;
}p[55];
bool cmp(project x,project y){
    return x.d<y.d;
}
int max(int x,int y){
    return (x>y)?x:y;
}
int min(int x,int y){
    return (x<y)?x:y;
}
int main(int argc, char** argv) {
    scanf("%d",&n);
    int maxd = 0; 
    for(int i=1;i<=n;i++){
        scanf("%d%d%d",&p[i].p,&p[i].l,&p[i].d);
        maxd=max(maxd,p[i].d);
    }
    sort(p+1,p+n+1,cmp);
    for(int i=1;i<=n;i++){
        for(int j=maxd;j>=p[i].l;j--){
            int k = min(j,p[i].d);
            if(k-p[i].l<0)continue;
            dp[j]=max(dp[j],dp[min(j,p[i].d)-p[i].l]+p[i].p);
        }
    }
    printf("%d",dp[maxd]);
    return 0;
}