paillier半同态加密学习

1.背景

《数据安全法》已于2021年9月1日起正式实施，两个月后《个人信息保护法》也开始施行。数据安全日益重要，密文计算也成为了工作中必不可少的内容。目前应用密码学领域的密文计算方案分三类：全同态（FHE）、部分同态（SWHE）和半同态（PHE）。FHE算法复杂性过高且目前效率较低，普遍应用的是半同态加密算法，今天就paillier半同态加密算法做一次深入学习。

2.算法方案步骤

2.1 秘钥生成

注：gcd(a, b)指a和b的最大公因数；lcm(a, b)指a和b的最小公倍数；

2.2 加密

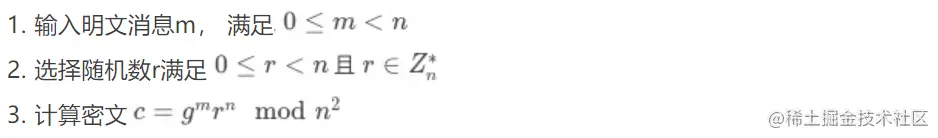
2.3 解密

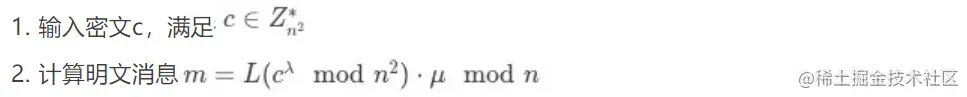
2.4 同态加

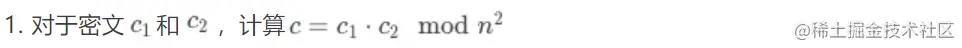
2.5 同态标量乘

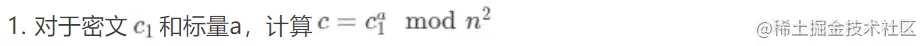
2.6安全性

Paillier方案满足加密方案的标准安全定义：语义安全，即在选择明文攻击下的密文的不可区分性（IND-CPA）。直观地说，就是密文不会泄露明文中的任意信息。方案安全性可以归约到判定性合数剩余假设（Decisional Composite Residuosity Assumption, DCRA），即给定一个合数n和整数z，判定z是否在n^2下是否是n次剩余是困难的。这个假设经过了几十年的充分研究，到目前为止还没有多项式时间的算法可以攻破，所以Paillier加密方案的安全性被认为相当可靠。

2.7加减乘除适用性

(正,正) 指的是 明文两个参数都是正数

参数对类型	加	乘
(正,正)	1	1
(正,负)	0	0
(负,正)	1	0
(负,负)	0	1

3.引用

Paillier半同态加密：原理、高效实现方法和应用
应用密码学 | Paillier同态加密算法简介
Paillier算法的原理和代码实现
paillier加密算法原理详解
同态加密：CKKS方案详解及一个python实现:TenSEAL（不定期更新）
快速幂运算
全同态加密实现算法代码.rar
python的PHE库python-reseal：Python完全同态加密（FHE）库
Gentry-开源