[C++]P3384 轻重链剖分(树链剖分)
[C++]树链剖分
预备知识
- 树的基础知识
- 关于这个本文有介绍
- 邻接表存图
- 线段树基础
- 最近公共祖先LCA
- 虽然用不到这个思想 但是有类似的
- 有助于快速理解代码
- 建议阅读这篇Blog
题意解读
题目描述
如题,已知一棵包含 \(N\) 个结点的树(连通且无环),每个节点上包含一个数值,需要支持以下操作:
操作 1: 格式: \(1\) \(x\) \(y\) \(z\) 表示将树从 \(x\) 到 \(y\) 结点最短路径上所有节点的值都加上 \(z\)。
操作 2: 格式: \(2\) \(x\) \(y\) 表示求树从 \(x\) 到 \(y\) 结点最短路径上所有节点的值之和。
操作 3: 格式: \(3\) \(x\) \(z\) 表示将以 \(x\) 为根节点的子树内所有节点值都加上 \(z\)。
操作 4: 格式: \(4\) \(x\) 表示求以 \(x\) 为根节点的子树内所有节点值之和
输入格式
第一行包含 44 个正整数 N,M,R,P,分别表示树的结点个数、操作个数、根节点序号和取模数(即所有的输出结果均对此取模)。
接下来一行包含 N 个非负整数,分别依次表示各个节点上初始的数值。
接下来 N-1 行每行包含两个整数 x,y,表示点 x 和点 y 之间连有一条边(保证无环且连通)。
接下来 MM 行每行包含若干个正整数,每行表示一个操作,格式如下:
操作 1: x y z;
操作 2: x y;
操作 3: x z;
操作 4: x。
输出格式
输出包含若干行,分别依次表示每个操作 22 或操作 44 所得的结果(对 PP 取模)
选自洛谷
算法思想
树链剖分
顾名思义 就是把树形结构改良成链状结构
这样可以通过线段树方便的维护
为了更好的讲解
这里先列举出几个概念:
- 重儿子 是指当前节点的所有儿子中子树最大的儿子
- 重链 全部由重儿子组成的链
接下来要进行的第一步
剖分树
剖分树需要有一个标准
这样才可以准确的知道这个树形结构是如何剖分的
这个标准就是 重儿子
这样就能剖出重链
将重链去掉后
再循环这个步骤
就能把一棵树剖成有限个链
举个例子
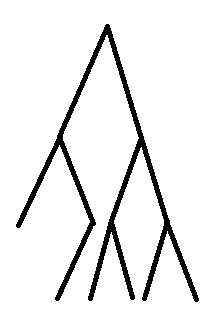
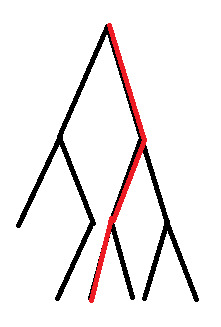

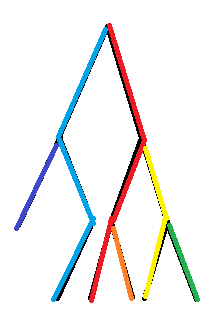
这样树就剖好了
线段树维护
树剖只是把树剖成的链条
但是还没能达到维护数据的目的
这个时候就可以用代码究极繁琐但是实用无比的线段树了
这个时候就需要创造能用线段树维护的条件了
我们首先先要对这棵树的节点按照链来重新排序号
然后再用线段树维护
具体方法详见代码讲解
代码讲解
这里先把变量的含义解释一下:
#define maxn 200007
#define mid ((l+r)>>1)
#define li i<<1
#define ri 1+(i<<1)
int n,m,root,mod;
//n m如题 root为根节点 mod为取余数
int deep[maxn],father[maxn],son[maxn],sub[maxn];
//deep代表深度 father代表父亲节点 son代表重儿子 sub代表子树的大小
int head[maxn],cnt,value[maxn];
//head cnt均为邻接表参数 value代表节点权值
//注 这里value是故意不存在邻接表里的
int top[maxn],id[maxn],value_sort[maxn];
//top 所在链的第一个节点 id新排序后的序号 value_sort新排序后的权值
struct Edge{//邻接表
int u,v;
Edge(int a = 0,int b = 0){
u = head[a];
v = b;
}
}e[maxn << 1];
struct Tree{//线段树
int l,r,sum;
int lazy;
}t[maxn << 1];
这个代码一共有个核心的函数
- \(Dfs1\)
- \(Dfs2\)
- 线段树相关函数
- \(Build\)
- \(push\)
- \(add\)
- \(search\)
- \(search\)_\(tree\)
- \(add\)_\(tree\)
我们依次来看
Dfs1
int dfs1(int u,int fa){
deep[u] = deep[fa] + 1;//u节点的深度比其父亲的深度大1
father[u] = fa;//存下u的父亲为fa
sub[u] = 1;//子树大小 先把自己的1给加上
int maxson = -1;//用来判定重儿子
for(int i = head[u];i;i = e[i].u){
int ev = e[i].v;
if(ev == fa) continue;
sub[u] += dfs1(ev,u);//让子树大小加上儿子节点的子树大小
if(sub[ev] > maxson){//若儿子i的子树大小比以往的都大
maxson = sub[ev];
son[u] = ev;
//那就更新状态
}
}
return sub[u];//返回u的树的大小
}
这是用来求 \(deep\) \(father\) \(son\) \(sub\) 的函数
这部分总体比较简单
注释就直接打代码上了
Dfs2
void dfs2(int u,int topf){
id[u] = ++cnt;
value_sort[cnt] = value[u];
top[u] = topf;
if(!son[u]) return;
dfs2(son[u],topf);
for(int i = head[u];i;i = e[i].u){
int ev = e[i].v;
if(!id[ev])
dfs2(ev,ev);
}
}
这部分是进行剖分
由于重儿子已经得到
那就沿着重儿子进行深搜就行了
注意这里是先进行dfs重儿子的递归再dfs其余儿子
因为我们是要把这条重链先剖出来
这里 \(for\) 循环里 \(if\) 的条件是:
!id[ev]
这说明这个变量还没有被赋值过
即还没有被 \(Dfs\) 到过
这样再进行深搜
线段树相关函数
这部分就是完全用了线段树
不需要改动
唯一注意的就是要加上取模
search_tree
int search_tree(int x,int y){
int ans = 0;
while(top[x] != top[y]){
if(deep[top[x]] < deep[top[y]]) swap(x,y);
ans = (ans + search(1,id[top[x]],id[x])) % mod;
x = father[top[x]];
}
if(deep[x] > deep[y]) swap(x,y);
ans = (ans + search(1,id[x],id[y])) % mod;
return ans;
}
这里的写法有点类似于LCA的树上倍增
来个例子:
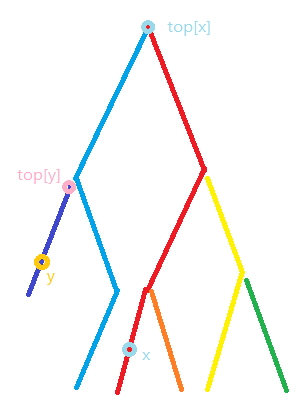
- \(top[x] != top[y]\)
其代表了 \(x\) 和 \(y\) 不处于一条链上的时候
就需要先把他们放到一条链上
这里我们对 \(top[x]\) 和 \(top[y]\) 的深度进行比较
让 \(x\) 处于深层
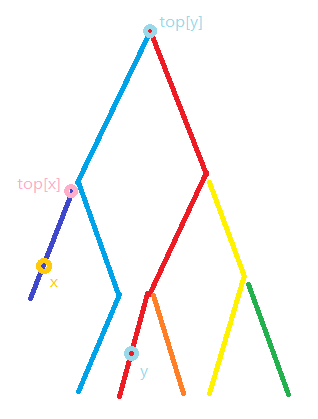
然后再把这个线段(黑色部分)的值加上
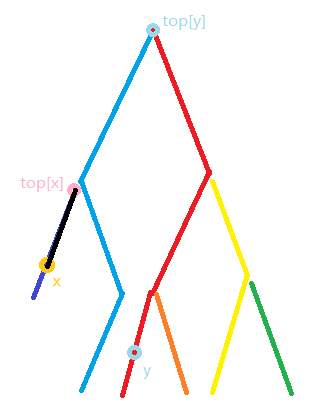
随后更新 \(x\) 的值
同时 \(top[x]\) 的值也会自动更新
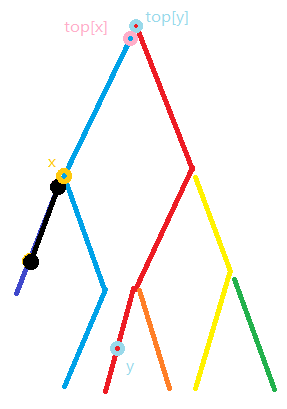
这里重复上述过程
把线段的值加上
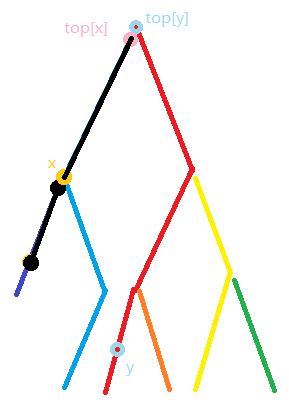
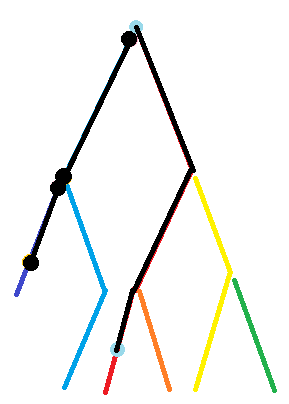
这样 \(x\) \(y\) 两点间的值就可以得到了
add_tree
void add_tree(int x,int y,int k){
while(top[x] != top[y]){
if(deep[top[x]] < deep[top[y]]) swap(x,y);
add(1,id[top[x]],id[x],k);
x = father[top[x]];
}
if(deep[x] > deep[y]) swap(x,y);
add(1,id[x],id[y],k);
}
这里的思想和 \(search\)_\(tree\) 的思想完全相同
就不再赘述了
吐槽
这个代码真的长
敲起来超费劲
Code
#include<bits/stdc++.h>
#define maxn 200007
#define mid ((l+r)>>1)
#define li i<<1
#define ri 1+(i<<1)
using namespace std;
int n,m,root,mod;
int deep[maxn],father[maxn],son[maxn],sub[maxn];
int head[maxn],cnt,value[maxn];
int top[maxn],id[maxn],value_sort[maxn];
struct Edge{
int u,v;
Edge(int a = 0,int b = 0){
u = head[a];
v = b;
}
}e[maxn << 1];
struct Tree{
int l,r,sum;
int lazy;
}t[maxn << 1];
void Read(){
int a,b;
cin >> n >> m >> root >> mod;
for(int i = 1;i <= n;i++) cin >> value[i];
for(int i = 1;i < n;i++){
cin >> a >> b;
e[++cnt] = Edge(a,b);
head[a] = cnt;
e[++cnt] = Edge(b,a);
head[b] = cnt;
}
}
int dfs1(int u,int fa){
deep[u] = deep[fa] + 1;
father[u] = fa;
sub[u] = 1;
int maxson = -1;
for(int i = head[u];i;i = e[i].u){
int ev = e[i].v;
if(ev == fa) continue;
sub[u] += dfs1(ev,u);
if(sub[ev] > maxson){
maxson = sub[ev];
son[u] = ev;
}
}
return sub[u];
}
void dfs2(int u,int topf){
id[u] = ++cnt;
value_sort[cnt] = value[u];
top[u] = topf;
if(!son[u]) return;
dfs2(son[u],topf);
for(int i = head[u];i;i = e[i].u){
int ev = e[i].v;
if(!id[ev])
dfs2(ev,ev);
}
}
void Build(int i,int l,int r){
t[i].l = l;
t[i].r = r;
if(l == r){
t[i].sum = value_sort[l];
return ;
}
Build(li,l,mid);
Build(ri,mid+1,r);
t[i].sum = t[li].sum + t[ri].sum;
}
void push(int i){
t[li].lazy = (t[li].lazy + t[i].lazy) % mod;
t[ri].lazy = (t[ri].lazy + t[i].lazy) % mod;
int mid_ = (t[i].l + t[i].r) >> 1;
t[li].sum = (t[li].sum + t[i].lazy * (mid_-t[i].l+1)) % mod;
t[ri].sum = (t[ri].sum + t[i].lazy * (t[i].r - mid_)) % mod;
t[i].lazy = 0;
}
void add(int i,int l,int r,int k){
if(l <= t[i].l && t[i].r <= r){
t[i].sum += k * (t[i].r - t[i].l + 1);
t[i].lazy += k;
return ;
}
if(t[i].lazy != 0) push(i);
if(t[li].r >= l)
add(li,l,r,k);
if(t[ri].l <= r)
add(ri,l,r,k);
t[i].sum = (t[li].sum + t[ri].sum) % mod;
}
int search(int i,int l,int r){
if(l <= t[i].l && t[i].r <= r)
return t[i].sum;
push(i);
int ans = 0;
if(t[li].r >= l) ans = (ans + search(li,l,r)) % mod;
if(t[ri].l <= r) ans = (ans + search(ri,l,r)) % mod;
return ans;
}
int search_tree(int x,int y){
int ans = 0;
while(top[x] != top[y]){
if(deep[top[x]] < deep[top[y]]) swap(x,y);
ans = (ans + search(1,id[top[x]],id[x])) % mod;
x = father[top[x]];
}
if(deep[x] > deep[y]) swap(x,y);
ans = (ans + search(1,id[x],id[y])) % mod;
return ans;
}
void add_tree(int x,int y,int k){
while(top[x] != top[y]){
if(deep[top[x]] < deep[top[y]]) swap(x,y);
add(1,id[top[x]],id[x],k);
x = father[top[x]];
}
if(deep[x] > deep[y]) swap(x,y);
add(1,id[x],id[y],k);
}
void interaction(){
int tot;
int x,y,z;
for(int i = 1;i <= m;i++){
cin >> tot;
if(tot == 1){
cin >> x >> y >> z;
add_tree(x,y,z%mod);
}
if(tot == 2){
cin >> x >> y;
cout << search_tree(x,y)%mod << endl;
}
if(tot == 3){
cin >> x >> z;
add(1,id[x],id[x]+sub[x]-1,z%mod);
}
if(tot == 4){
cin >> x;
cout << search(1,id[x],id[x]+sub[x]-1)%mod << endl;
}
}
}
int main(){
Read();
dfs1(root,0);
cnt = 0;
dfs2(root,root);
Build(1,1,n);
interaction();
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号