prim算法

输入


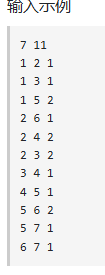
这种点之间的距离创造邻接矩阵来储存横纵坐标节点的距离。

这些vector的初始化都要赋值（一般INT_MAX，没有边则保留）

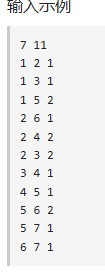
储存边的权值：

    vector<vector<int>> dis(n+1,vector<int>(n+1,10001));
        int x,y,k;
        while(e--){
            cin>>x>>y>>k;
            dis[x][y]=k;
            dis[y][x]=k;
        }

两个需要更新维护的数组：
已经加入了tree的和因为cur更新而更新的mindist。

vector<int> mindist(n+1,10001);

vector<bool> visited(n+1,false);

关键三部曲：

for(int i=1;i<n;i++){

        int cur =-1;
        int min_val=INT_MAX;//每次更新完后需要重新计算最短距离来寻找下一个cur

        //1.对每个i更新cur（离tree最近的点）
        for(int j=1;j<n+1;j++){
            if(!visited[j]&&mindist[j]<min_val){
                cur=j;
                min_val=mindist[j];
            }
        }


        //2.树加入cur
        visited[cur]=true;

        //3.因为cur更新了，与之相关的mindist也需要更新
        for(int v=1;v<n+1;v++){
            if(!visited[v]&&dis[cur][v]<mindist[v]){
                mindist[v]=dis[cur][v];
            }
        }
}

全代码：

#include<iostream>
#include<vector>
#include <climits>

using namespace std;
int main() {
    int v, e;
    int x, y, k;
    cin >> v >> e;
    // 填一个默认最大值，题目描述val最大为10000
    vector<vector<int>> grid(v + 1, vector<int>(v + 1, 10001));
    while (e--) {
        cin >> x >> y >> k;
        // 因为是双向图，所以两个方向都要填上
        grid[x][y] = k;
        grid[y][x] = k;

    }
    // 所有节点到最小生成树的最小距离
    vector<int> minDist(v + 1, 10001);

    // 这个节点是否在树里
    vector<bool> isInTree(v + 1, false);

    // 我们只需要循环 n-1次，建立 n - 1条边，就可以把n个节点的图连在一起
    for (int i = 1; i < v; i++) {

        // 1、prim三部曲，第一步：选距离生成树最近节点
        int cur = -1; // 选中哪个节点 加入最小生成树
        int minVal = INT_MAX;
        for (int j = 1; j <= v; j++) { // 1 - v，顶点编号，这里下标从1开始
            //  选取最小生成树节点的条件：
            //  （1）不在最小生成树里
            //  （2）距离最小生成树最近的节点
            if (!isInTree[j] &&  minDist[j] < minVal) {
                minVal = minDist[j];
                cur = j;
            }
        }
        // 2、prim三部曲，第二步：最近节点（cur）加入生成树
        isInTree[cur] = true;

        // 3、prim三部曲，第三步：更新非生成树节点到生成树的距离（即更新minDist数组）
        // cur节点加入之后， 最小生成树加入了新的节点，那么所有节点到 最小生成树的距离（即minDist数组）需要更新一下
        // 由于cur节点是新加入到最小生成树，那么只需要关心与 cur 相连的 非生成树节点 的距离 是否比 原来 非生成树节点到生成树节点的距离更小了呢
        for (int j = 1; j <= v; j++) {
            // 更新的条件：
            // （1）节点是 非生成树里的节点
            // （2）与cur相连的某节点的权值 比 该某节点距离最小生成树的距离小
            // 很多录友看到自己 就想不明白什么意思，其实就是 cur 是新加入 最小生成树的节点，那么 所有非生成树的节点距离生成树节点的最近距离 由于 cur的新加入，需要更新一下数据了
            if (!isInTree[j] && grid[cur][j] < minDist[j]) {
                minDist[j] = grid[cur][j];
            }
        }
    }
    // 统计结果
    int result = 0;
    for (int i = 2; i <= v; i++) { // 不计第一个顶点，因为统计的是边的权值，v个节点有 v-1条边
        result += minDist[i];
    }
    cout << result << endl;

}