2025做题
01-18
居然到18号才开始写日记/qd/qd
- 道路の建設案
曼哈顿距离不好做,考虑转换成切比雪夫距离,然后就把绑定的两维的限制变成两个一维的限制了,然后二分答案,对于每个二分的答案x,都把当前遍历到的值到\(x_i-x\)都放到set里,然后对于y这一维直接在x里查就行了,如果有的话那res就加一,最后看看有没有达到限制就行了。转换挺巧妙的。 - k-d-sequence
我看题解才会的。首先先把序列都对d取模,那么合法的就一定是连续一段一样的值,然后考虑对一段模完一样的值都变成模d的余数,那显然合法的就是这里的一段排序之后max-min+1-(l-r+1)<=k,然后转换一下就变成了max(L,R)−min(L,R)+L≤k+R,考虑枚举r,然后发现这玩意可以用线段树维护一下,具体地,肯定是这个数的余数大于前面的数的话那这个数就要进线段树更新,然后发现这玩意不好直接维护,用一个单调栈就好了,难想又难写。 - Pudding Monsters
考虑每行每列只有一个布丁,所以我们直接按x轴压成一维,然后就是上一题了。 - 上帝造题的七分钟 2 / 花神游历各国
胡扯题,发现\(10^6\)开6次根号就到1了,所以可以把全是1的区间打个标记,如果要修改的区间全是1的话就不用改了,然后用改的直接暴力改,反正用不了多少时间,然后就是普通线段树了。
01-20
- Blocking Elements
注意到复杂度,只能\(O(nlogn)\),所以考虑二分,二分答案,然后发现可以用第二条作为限制,只要这一段的和大于二分的答案了就把这个点变成分界点,最后判断分界点的和是否合法,但是显然这样很假,甚至过不了第二个样例,因为第二个样例是把第一个变成分界点,然后就遇到困难了,发现不知道在哪开始作为第一个分界点的时候答案是最优的,所以就想到可以dp,把每一个点是分界点的情况都算一下,具体地,设\(f_i\)表示第i个选成分界点的最小价值,转移就是在\(i-1\)到尽量靠前的满足这一段的和小于二分的答案,在这一段里找到上一个分界点,使值最小。然后发现这样dp复杂度是\(O(n^2)\)的,但是发现那个上一个的最小的分界点的那段可以做dp的时候用单调队列维护,所以dp就愉快的变成\(O(n)\)的了,总复杂度是\(O(nlogn)\)。 - Magic Matrix
注意到数据范围很小,前两个限制可以暴力做,后面一个发现很难做,但是发现如果一直把限制递归下去,发现其实就是在一个图上的任意一个环上的任意一条边都满足这条边以外的环上的其他边的最大值比他大(这玩意能想出来的都是神人了),然后就发现如果对于边排序,只要当前遍历到的这条边不在环里就是合法的,反之就不合法,然后就做完了,复杂度可以近似估算为\(O(n^2logn^2)\) - Mind Control
一眼题,没什么写的必要。 - Flowerpot S
考虑二分答案,然后发现是\(O(n^2logn)\)的,过不去,考虑优化,发现可以提前用单调队列处理出来二分的答案的长度里的最大值和最小值,然后直接\(O(n)\)扫一遍判断合法不合法就行了 - 萌萌哒
神人题,发现很容易有一个并查集的暴力,就是对于每个限制区间暴力并查集合并,然后最后直接看有几个不同区间就行了,但是要\(O(n^2)\),然后就不会了,但是感觉已经到头了,应该得数据结构优化,但是想了很久也只能想到线段树,但是不会怎么线段树+并查集,所以就不会了,看了题解之后才知道原来可以用倍增,然后局势就豁然开朗了,直接对于限制下放到下面两个区间,然后最后统计答案就行了。 - XOR Tree
这种树上异或的玩意显然第一眼就能想到转换成到根的路径,然后就有一个很显然的\(O(n^2logn)\)暴力,具体地,枚举lca,然后对于子树内如果有两个点的异或再异或上lca等于0的话就改lca,而且一个lca最多改一次。然后发现这玩意很可以用树上启发式合并,然后复杂度就能过了。
01-21
- Xor-MST
想到最小生成树,但是发现代价是两个点的异或和,然后思考怎么能把任意两个点的这玩意排序下来,想到01-Trie,发现建出01-Trie之后就从底下到上面,从左到右依次选lca就行了,因为左边的显然更小,而且lca越靠下异或和越小,就可以直接做了。 - Data Center Drama
发现出边+入边是偶数这玩意的充要条件就是这玩意是个欧拉回路,所以就直接对于总度数是奇数的点之间连边就行了,然后考虑对于一个边长是偶数欧拉回路我们可以直接\(a->b<-c->d<-...<-a\)就可以保证这玩意是入度和出度都是偶数了,如果是奇数条边的话就连个自环就行了。 - Hemose in ICPC ?
看到范围和12次,而且显然一个区间的子区间的查询值肯定小于等于这个区间,所以感觉可能是二分,于是往可以二分性的一维东西上想,又想到能把图转换成数列的玩意,想到了欧拉序,然后就出正解了,直接跑欧拉序,然后对于这个序列先询问一次最大值,然后直接二分就行了。 - [ICPC2022 Xi'an R] Tree
不难观察到操作1就是删掉一个链,操作二就是删掉所有叶子节点,然后发现如果想只用操作1把当前的树删没的话就是当前的叶子节点个数,然后就很好做了,直接每次删掉当前的所有叶子节点再重新计算哪些是叶子节点就行了,在这个过程中算ans的最小值。
然后又在南外上写了几道区间dp
01-22
- Omkar and Last Floor
发现肯定同一列的1越多越好,考虑区间dp,设\(f_{l,r}\)表示在l到r列的得分最大值,考虑l,r中间的某列k,考虑跨过第k列的且区间在l,r之内的区间,把他们的1都放到第k列就行了,然后进行区间dp就好 - P4766 [CERC2014] Outer space invaders
发现跨过某个时间的所有区间肯定用这些区间里最大的R来消灭,考虑区间dp,\(f_{l,r}\)表示把区间包含的所有区间都消灭的最小代价。考虑这个区间里包含的R最大的值所在的区间,然后在这个区间里找花费R能消灭的最大的区间,但是需要离散化。 - P7297 [USACO21JAN] Telephone G
暴力很简单,但是\(O(n^2)\),发现优化很难,根本不会,然后看到很小的k还没用,所以想到可能跟k有关系,于是想到可以用分层图其实是在做分层图专题,考虑建\(k-1\)层,每层内部i和i+1连双向边权为1的边,我们想要对第k+1层求答案,所以把\((b_i,i)\)向\((k+1,i)\)连一条边权为0的单向边,如果\((b_i,j)\)能传递的话,就建立\((K+1,i)\)向\((j,i)\)的边权为0的单向边,然后对于起点是(k+1,1),终点是(k+1,n)的最短路就行了。 - P10819 [EC Final 2020] City Brain
能推出来式子的都是神人了。首先先跑一个最短路求出来任意两点之间的最短路,然后发现要求的两条道如果有重合的地方,那重合的地方肯定连续,因为如果不连续的话那两个连续点中间的不连续部分肯定有一条小于等于另一条,显然走更小的更优。所以考虑枚举重合的起点和终点,然后算出来对于每个重合的长度对应的最小的到起点和终点的最短路,现在考虑在哪用技能更优,发现这玩意列出来之后是个单峰函数,于是想到三分,三分完就是答案了。
01-23
- Arpa’s letter-marked tree and Mehrdad’s Dokhtar-kosh paths
发现他只给了22个字母没给26个,于是猜到应该跟状压有关系,所以直接先把字母压成状态,然后又看到任意序列的回文,所以猜想其实回文长啥样不重要,联想到回文的性质,发现其实只要最多只有一个出现单数次的字母就行了,加上之前的发现其实就跟异或一样,然后直接先把路线异或转成到根的异或,发现其实可以用很常规的思想转换为枚举点,然后看这个点的子树中的最大值,然后分成是否经过这个点,然后就可以\(O(n^2)\)做了,发现时间复杂度还是不够,于是用dsu on tree - P3224 [HNOI2012] 永无乡
很套路啊,线段树合并+并查集就行了但是我其实早就忘了咋写线段树合并了 - Two Permutations
这个想不到,这个真难,首先先把a序列的哈希求出来,然后通过推式子之类的玩意我们可以发现其实如果给a都加x的话那么整个数列的和的哈希就变成了\(x\sum_1^np^{n-i}\),然后发现其实后面的求和是可以预处理出来的,所以对于加的x我们可以直接\(O(1)\)求出来,所以我们就可以把x从0到m-n加入a之后的哈希值都求出来,然后放进map里,然后考虑b怎么查,发现a是一个排列,所以可以把b先排个序然后按大小依次加入之前的在数组中的位置,然后考虑每次加入一个数之后当前有没有能对应上map里的哈希值的,如果加入了之后长度大于n了就删去最小的,然后发现这玩意很不好实现,于是考虑用一个权值线段树维护一下,就做完了 - [ABC304E] Good Graph
弱智题,并查集+map直接查就行了
又在南外写了几道区间dp
01-24
- Misha and LCP on Tree
这题挺难写的,但是思路还行,考虑两个序列的最长公共前缀,发现其实直接二分+哈希就行,但是现在转到树上了,所以比较困难,现在想怎么用\(log\)时间的玩意做,发现其实可以树剖,然后一段一段的哈希比较,如果在这一段的哈希不一样了就在这两段上二分就行了。 - P1723 高手过愚人节
这题其实挺简单的,想写这个的原因是我本来用的是二分+哈希想水过去,结果最后被卡了,才换的马拉车,以后有复杂度更优的尽量用更优的。 - P1600 [NOIP2016 提高组] 天天爱跑步
绷不住了,纯线段树合并水题,但是我这个废物调了+inf年。
01-25
先复习了一下莫队,写了两道模板题
- P4462 [CQOI2018] 异或序列
这种形式直接想到莫队,但是莫队的那个记录出现次数的玩意其实不仅可以当某个值用,也可以当桶用,别的直接按照莫队正常方式写就行了 - P3758 [TJOI2017] 可乐
发现n很小,t很大,感觉应该和图论啥的就没啥关系了,所以考虑到\(logt\)的做法,联想存图的邻接矩阵,想到矩阵,然后就很开朗了,直接矩阵快速幂就行 - P6374 「StOI-1」树上询问
考虑到如果z不在x到y的路径上,肯定不行,如果z就是lca的话那显然答案就是n-(x对应的那条路的lca的孩子的子树的大小)-(y的那条路的lca的孩子的子树的大小),然后考虑如果z在x或y到lca的路径上,那我们答案可以类比过来就是n-(x/y的那条路的lca的孩子的子树的大小)-(n-sz[z]),然后就没了,但是有一个比较强的玩意就是用dfs序判断x是否在z子树里的玩意是这道题最大的收获
还做了几道比较水的题。
02-03
补了补之前的题。
- Maximum Rating
发现有个上界和下界,然后发现其实上界和下界中间的都可以达到,所以可以直接权值线段树。 - Expanding Array
利用异或无限扩展(x,y),是进行“宽度优先搜索”的先决条件;于是你也不能认为,出现了相同的数就可以终止搜索,因为它可能还会对之后的结果产生影响
更轻巧的思维方式是,考虑011/101,考虑000~111的所有数字是否可以构造出来,发现可以,于是用STL来判个重就行
02-04
省选考试,啥也不会,爆。
- HDU6410 序列期望

考场上想到了应该是\(O(Vn)\)的了,写出来是枚举h然后对每个区间算了,但是没写对,考完之后改了改取模和实现细节就对了。
一定要仔细看题!一定要理解如何递推! - 牛客 分糖果

赛时能写出来的是神人,赛时想到了应该是个容斥,也想到从链开始转化为环了,然后就推出来了个非常离谱的容斥,甚至还过了很多样例,结果最后错了。
首先肯定是破环为链,然后考虑容斥,显然是所有情况-至少一个连续一样的+至少两个连续一样的……,然后就假定这个序列里有k个连续的相等的段,然后这一段全部取值相等的数里最大的取值肯定就是\(min_{i=l}^ra_i\),设\(f_i\)表示到i的时候的答案,然后加个容斥系数之类的,就能发现式子是\(f_i=\sum_{j=1}^i(-1)^{i-j}f_{j-1}min_{k=j}^ia_k\),然后考虑如何把链变成环,发现只需要考虑最后一位和第一位是否相等就行了,然后发现这样不好定这两个点的所在段的最小值,于是钦定第一个是序列中最小的,然后就可以直接减掉相同情况了。然后发现这玩意是个\(O(n^2)\)的,于是考虑优化,考虑把\((-1)^{i-j}\)转化成\((-1)^i*(-1)^{-j}\),然后考虑用单调栈优化\(\sum_{j=1}^if_j(-1)^{-j}min_{k=j}^ia_k\)这一坨,发现可以,然后就能做到\(O(n)\)了
02-05
- P10597 BZOJ4665 小 w 的喜糖
一看到每个糖都与原来不同就想到应该能用二反之类的东西搞出来,首先我们设\(f_i\)表示至少有i个人和原来的糖果一样,别的不考虑的情况,那二反一下,答案就是\(g_0\),然后考虑\(f_i\)咋求,发现不知道从i到i+1的时候不知道放到哪,所以考虑多加一维,设\(dp_{i,j}\)表示前i种颜色j个相同的位置其他随便放的情况,发现可以这么转移
其中\(cnt_i\)表示第i个颜色的个数,sum表示1~i颜色的个数和,转移的方程式很好想,可以自行理解,然后就能做了。
- P6076 [JSOI2015] 染色问题
发现这玩意很难一块搞,考虑一个一个搞,首先先考虑每种颜色至少出现一次的限制,设\(f_i\)为颜色最多有i种的情况,然后之后容斥一下就是答案,考虑用行和列的限制去求\(f_i\),首先枚举一个j表示最多使j行满足条件,然后就肯定有一个\(C_n^j\)和一个容斥系数\((-1)^{n-j}\),这个可以根据组合意义去推,然后是对于某一列选中的j行,每格都有i+1(空白)的情况,所以一共的情况就是\((i+1)^j\),但是全部空白肯定是不行的,所以还要减一,最后有m列,所以还有个m次幂,所以总的就是
- P10596 BZOJ2839 集合计数
感觉很像反演,所以往那里考虑,首先设\(f_i\)表示选中的集合至少交i个元素的选集合方案数,有:\(f_i = C_n^k (2^{2^{n-k}}-1)\)
然后就直接二项式反演就行了。
晚上是比赛,2.8h时长+没有任何大样例+题目样例过水导致T1+T2都忘却了有多组数据要清空数组和变量,导致一共挂了160pts,T1T2加起来只需要补两行的清空就能拿到的160分我却没加,引以为戒,以后多想想,养成好习惯。但是比较不好的一点就是其实要是好好想的话T3T4我觉得我能拿70+92的,但是时间太短了,所以以后还是希望来点正经的比赛。
T1T2完全不用讲了,比较简单,一个小思维题一个类似折半搜索一类的玩意,只用枚举全排列然后用初始矩阵和答案矩阵直接找就行了,好像爆搜+剪枝也能过,有点水了。。下面是T3T4的原题
- P6651「SWTR-5」Chain
先考虑Subtask3,发现其实只需要维护入度为0的点到i的路径数量就行了,转移就是\(f_v+=f_u\),然后转移的时候不能走\(c_i\),最后统计出度为0的合法的点的贡献就行了,算是个暴力但是赛时暴力居然挂了20,再考虑k=1的点,发现其实可以再维护一个从i出发到出度为0的点的数量,然后发现答案其实就是\(sum-f_{c_1}*g_{c_1}\),其中\(sum\)表示一个点都不删的答案,到这里其实就比较能想到正解了,就是考虑容斥,发现可以利用拓扑序,对于每个y只需要把它的\(f_y\)减去拓扑序在它前面的x的\(f_x*h_{x,y}\)就行了,最后再乘上\(g_y\)再用总答案减去就行了,期中\(h_{x,y}\)表示的是x到y的路径数量。但是这道题要注意的点是一定要把代码写的常数小一点,要不会一直被卡。 - P6378 [PA 2010] Riddle
一个很显然的思路是直接对于每条边连着的两个点去连另一个点的反点,然后对于每一组点都连别的点的反点,然后跑2-SAT,最后判断自己和自己的反点是否在同一个强连通分量里就行了。但是这样建图的空间是\(O(n^2)\)的,根本不行,会炸,但是居然能拿到92的高分,然后考虑优化建图,这优化方式反正我想不出来,能想出来的都是神人。你考虑原来的建图方式是这样的

但是很多,所以考虑建辅助点来减少连边但是保证和原来的效果一样,发现可以这么建

这样建发现和原来是等效的,所以只需要把原来的图这么建就行了。
02-06
上午改了昨天晚上考试的题,下午和晚上写容斥。
- Devu and Flowers
先考虑如果瓶子里的花是无限的,那有多少种选的方案,发现是\(C_{s+n-1}^{n-1}\),然后考虑容斥掉不合法的,答案即为:
但是发现这玩意直接做复杂度是很爆炸的,所以考虑怎么优化。然后发现n很小,感觉应该是二进制枚举啥东西,于是就想到了对于\(0<=x<=2^n-1\),它的二进制中共有p位为1,然后就可以用这玩意来表示上面的一项,然后这样做的话复杂度就对了,但是求排列组合的时候可能在\(C_x^y\)中x很大,所以变换一下,发现可以把它和排列的转换搞出来,再递推做,就行了。
- Gerald and Giant Chess
考虑从起点到任意一个点的方案数,为\(C_{x+y-2}^{x-1}\),然后考虑怎么算到一个黑点且不经过它之前的黑点的方案,那肯定要先按x和y的大小排序,设\(f_i\)表示从起点到第i个黑点且不经过别的黑点的方案数,发现其实就是总方案数-在它左上角的j:\(f_j*C_{x_i-x_j+y_i-y_j}^{x_i-x_j}\),然后就可以处理出来每个\(f_i\)了,发现最后的答案就是:
- Make It One
首先通过观察发现从2开始的质数一直乘到17就大于300000了,这一共才7个质数。然后开始思考这道题,发现我们可以先考虑选x个数,然后让他们的公约数为i的方案为\(f_{x,i}\),然后先不管x,因为x这层与x-1和x+1没有任何关系,所以可以在最外面枚举这玩意,然后我们发现其实\(f_i\)求起来还是挺容易的,我们先预处理一个\(g_i\)表示i在这个数列中的倍数个数,这东西的处理是个调和数级别的,具体地,\(g_i=\sum_{j=2,ij<=V}g_{ij}\),然后倒着预处理就行了,然后推如何求\(f_i\),首先想到要想这几个数的最大因数是i,那必然他们要有个i为公因数,然后考虑减去最大公因数是i的倍数的,就是\(f_i\)了,所以最后求\(f_i\)的公式就是\(C_{g_i}^x-\sum_{j=2,ij<=V}f_{ij}\),然后倒着推就行了。
02-07
上午考南外的模拟赛,炸飞了,因为不知道树形dp自带的少\(O(n)\)的复杂度,以至于对着自己的正确代码想了一整个考试,最后也没打别的题的暴力,也没交题。
- P7201 [COCI 2019/2020 #1] Džumbus
发现其实这就是个树形dp,设\(f_{u,j,0/1}\)表示现在在j点,收益是j,当前点选或不选,发现选的方案很好转移,直接\(f_{u,i+j,0}=min(f_{u,i+j,0},f_{u,i,0}+min(f_{v,j,0/1}))\),但是好像1的比较复杂,但是可以慢慢推,首先考虑从\(f_{u,i-1,0}\)转移过来,即\(f_{u,i+j,1}=min(f_{i,i+j,1},f_{u,i-1,0}+a_u+min(f_{v,j-1,0}+a_v,f_{v,j,1}))\),再考虑从\(f_{u,i,1}\)转移过来的发现可以分成j选、不选和之前不选现在选了的,就行了。

就是这样,然后就可以直接转移了,然后答案可以\(O(qn)\)处理也可以直接先推一下后缀最大值,然后直接二分,但是其实我觉得2e8也能过。
T2不知道原题是啥。

首先有个没有操作3的40分,这个很好拿,直接看最后翻转好还是不好就行了,然后考虑操作3。
发现可以处理出来每个可能序列的逆序对数量,由于n很小所以可以求出来,然后就没有了,难度在于没人能想到要用__int128
02-08
今天做了很多比较简单的期望,主要是之前基本没做过。
- P6669 [清华集训 2016] 组合数问题
发现只会1000的,所以考虑看题解。发现可以用卢卡斯定理,然后发现这玩意其实可以拆开每一位,然后进行连乘,即为答案,然后发现这样的话其实只有18位,然后考虑按位进行dfs,每次只需要看当前位对于这两个数枚举的数只要i<j就是1,反之就是0呗,然后就直接dp就行了。 - P4707 重返现世
绷不住了,会的是神人。首先考虑min-max容斥,然后考虑dp,记\(f_{i,j,k}\)表示前i个数,选中的集合大小位j,\(\sum_{选中的i} a_i = k\),转移就很简单:
然后考虑优化复杂度,考虑到min-max容斥最后计算答案的时候的系数是\(\sum C_{T-1}^{k-1}(-1)^{T-k}\),和上面的递推式两种的递推方法结合一下,然后发现其实这俩玩意的转移是非常相似的,都是(i-1,j)和(i-1,j-1),然后就可以一起转移了,考虑增加一个维度k在计算系数:
- FAVDICE - Favorite Dice
其实直接考虑dp就行了,设\(f_i\)表示现在已经投了i面了的期望方案数,然后转移方程就很简单了:
移项,\(f_0\)即为所求
- Game on Tree
考虑一个排列就是操作方案,然后考虑怎么会合法,其实就是一个点的祖先在它后面就行了,然后就发现其实这个序列合法的情况就是\(dep_u\),然后总的答案就是\(\sum \frac{1}{dep_i}\) - P4316 绿豆蛙的归宿
直接宽搜就行了,设\(f_i\)表示从1到i点的期望步数,然后发现这玩意不能直接推,因为我们不知道从1到i的概率是多少,所以再记一个\(g_i\)就行了:
值得注意的是,不能用dfs的,因为如果dfs就不可能正确的算\(g_i\)了。
- P5104 红包发红包
第i个人抢到钱的大小的期望显然是x/2,快速幂就做完了。 - P6046 纯粹容器
n小的没边了,考虑比较大的复杂度,先对于每个i,找到它左右第一个比它大的数的下标,如果这个数想被删除,那要么li中间全没了,要么ir,然后就直接考虑左,右边的方案,再减去两边的方案就行了,最后把答案累加。 - Vasya and Magic Matrix
显然要先根据w的大小排序,然后对于w分成若干块,每块的答案显然一样,更新也应该在这一块全都处理完之后再更新,然后把式子列出来:
其中,s是i前比i的w小的个数,然后把这坨展开,发现f_j,x_j,y_j,(x_j)2,(y_j)2可以前缀和维护,然后就做完了。
02-09
- Fish
发现n很小,直接状压,然后考虑枚举的每个状态,0就是现在这个鱼死了,1就是还活着,然后枚举0的每一个和1的每一个,然后考虑枚举到的这个1的杀掉了枚举到的0的,然后这个1的杀死这个0的还有一个概率,所以复杂度是\(2^nn^2\)。 - Let's Play Osu!
感觉比较无敌,先考虑如果贡献是1的话,那就比较简单了,\(f_i=(f_{i-1}+1)*p_i\),然后考虑如果是平方,该怎么做,发现\((x+1)^2-x^2=2x+1\),然后就比较能做了,考虑再维护一个\(g_i\)表示从1到i都是1的期望,然后就很好转移了:
- P1850 [NOIP 2016 提高组] 换教室
这题也是无敌,能评蓝。。直接考虑\(f_{i,j,0/1}\)表示在i,加上当前的一共换了j,当前换没换。但是转移非常长,就对于前面和现在的概率直接乘就行了。 - P2221 [HAOI2012] 高速公路
很2b,仔细想想就会发现根本不是期望,就是求这个区间的后缀和除\(C_{r-l+1}^2\)就行了,直接线段树维护就行了。 - P3750 [六省联考 2017] 分手是祝愿
其实仔细想想就能发现最优的关灯顺序肯定是从大到小看是否开着,要是开着就关上就行了。然后就考虑期望,设\(f_i\)为关到i的期望次数,即为\(f_i=\frac{i}{n}+\frac{n-i}{n}(f_{i-1}+f_{i}+1)\)然后就行了。 - P3239 [HNOI2015] 亚瑟王
还行,差点想出来。先考虑第i张卡被用的概率为\(dp_i\),答案就是\(\sum_{i=1}^{n}dp_id_i\),然后考虑怎么求,感觉肯定有个\(n^2\)的dp,所以设\(f_{i,j}\)表示r轮中前i个选了j个的方案数,那\(dp_i\)的式子就呼之欲出了:
但是现在还差dp的转移,但是发现这玩意其实也很简单,要么从\(f_{i-1,j}\)转移过来,要么从\(f_{i-1,j-1}\)转移过来,前面那个没选上,这个是选上了,把概率乘一下就行了。
02-15
我太菜了,一整个晚上才好好学会了树上启发式合并和点分治。
- CF600E Lomsat gelral
发现求的东西跟子树有关系,所以想到dsu on tree,然后发现其实就是板子 - P4149 [IOI 2011] Race
发现是求路径上的东西,所以考虑吧点分治,然后发现其实就是板子
剩下的时间写了点南外的期望专题
02-19
- Mocha and Diana (Hard Version)
首先容易发现加边的顺序是对答案没有任何影响的。然后考虑固定一个点,先把两个森林里的相同的点的所在的连通块都和这个点不联通的都和这个点连边,这样的话第一个森林里和这个点没有联通的连通块中的点肯定在第二个森林里和这个点联通,反之亦然,然后发现现在我们只需要从两个剩下的里面每个随意拿出一个连边就行了,因为左边的与固定的点不联通的在右边肯定联通,反之一样,所以这两个集合里的点肯定在两个连通块里都没有交集。
02-20
- Cheap Robot
设\(dis_u\)为从最近的一个加油站到u点的最小代价,考虑从任意一个加油站到u,只要能到且到的时候剩余的大于\(dis_u\),那代价一定是\(dis_u\),因为你到了之后可以从u再走到那个消耗最小的加油站再回来,这样代价就是\(dis_u\)了,然后你推一下式子。

然后你就发现了,其实答案就是\(max(dis_u+dis_v+w_{i,j})\),然后很显然的是这个东西肯定也在最小生成树上,因为如果不在就有更优的了,然后只需要预处理出来这个最小生成树再对每次询问跑倍增就行了。现在难点来到求\(dis_u\),你发现如果对每个加油站都求一遍单源最短路时间复杂度会炸,所以就建一个超级源点连上所有的加油站再从超级源点开始跑就行了。 - Move and Swap
容易得到一个\(O(n^3)\)的dp,\(f_{i,j}\)是红的在i,蓝的在j,然后你枚举蓝的从哪里转移过来就行了。考虑怎么优化,发现蓝的在哪并不重要,因为它可以从上一层任何位置转移到这一层任何位置,所以只枚举红色在的位置,如果不交换那就直接比较和这层最大值和最小值分别做差,取最大值和上一层更新这一层就行了,但是发现如果交换的话就得枚举j了,这显然是无法接受的,我们先考虑把交换的式子列出来

然后我们发现这玩意其实只是这一层对这一层的转换有影响,所以可以每层先记录两个的最大值再更新,然后就做成\(O(n)\)了 - Complete the MST
发现最优的肯定是只替换一个边,然后分讨,如果有一个环,这个环上没有被赋值的,那肯定往这个环上换一个这个边就行了,最小生成树的值不变。然后看没有环的话怎么办,发现你就对于每两个连通块直接暴力替换然后找哪个最优就行了 - Towers
我感觉这道题是最难的。考虑肯定叶子放是最优的,我们以 \(h\) 值最大的为根,那么就至少要在两个子树里有 \(h_rt\),对于其他点,只要在子树内存在不小于自身 \(h\) 值的就可以了。然后直接对于每个点做就行了,但是感觉很难想到。。。 - Xorcerer's Stones
设\(f_{i,j}\)表示在i,子树里异或和为j的最小代价就行了,但是要输出方案数,所以我们把这个里面记录转移到它的两个下标,最后直接递推往前输出就行了。然后考虑到对于子树大小是奇数的做和不做是一样的,又考虑到一个点如果做了,那它的孩子们就不可能做了。然后考虑是否转移,分两类就行了。具体为\(f_{i+1,j}=f_{i,j}\),这是不做的,\(f_{i+sz_i,j^b_i}=f{i,j}\),这是做的。
02-23
- Up and Down the Tree
你发现如果u里叶子节点距离u小于k的话那就能无损跳出。

其中\(f_u\)表示跳进u的子树里的贡献值,然后答案就是从根到任意一个叶子节点的最大值。 - Strange Operation
发现对怎么删计数很难,所以考虑记最后的可能方案。考虑记录两个1之间的零的个数,发现一段1不可能全消掉,然后考虑这一位选填1还是0,如果是1的话就到下一段记录,如果是0且现在填的0的连续个数大于原数列的了的话就找后面第一个段长大于等于当前连续个数的段,然后跳过去转移,这个第一个大于的可以用单调栈求出。难死了,想不出来 - 外星人
首先发现如果你模了x,那你再模比x大的就没有任何用了,所以那部分可以乱模。然后先考虑怎么计算最大的传递值,发现只需要\(f_i \to f_{i \ mod b_j}\)就行了,最后直接找最大的。现在考虑怎么计算次数,发现其实能和前面那个一起转移。你考虑先把数组排序,从i转移到比它小的j的贡献其实就是 \(\frac{(N_i-1)!}{N_{i\mod a_j}!}\),N表示前缀和。然后直接转移就行了。 - Expected diameter of a tree
容易想到概率是诈骗,其实答案就是两棵树的所有连边方式的直径长度和/(siz_x * siz_y),然后发现重复的两棵树的询问的答案是相同的,所以考虑用map记录,现在考虑怎么计算答案,考虑某种连边的直径是啥,发现很显然是\(max(len_x, len_y, mx_x+mx_y)\),其中前两个就是这两个玩意所在的树的直径,后面那个就是树种距离x最远的点到x的长度,前两个是固定的,所以变的其实就是后面俩,考虑使用双指针解决,然后发现可以二分,就可以做了,现在感觉复杂度是\(O(n^2logn)\),但是其实不然,因为大小小于\(\sqrt{n}\)的树的个数只有\(\sqrt{n}\)个,所以本质不同的询问只有n个,而且有记忆化,所以最后复杂度就是\(O(n\sqrt{n}logn)\)
03-06
- Transmitting Levels
很好的一个思路,首先发现如果能走肯定不会开新的,所以可以对于每个k先用双指针求出来从每个点开始不从新开始的能到的最远的点,记为\(to_i\),然后考虑暴力,肯定就是枚举从哪个点开始然后跳一圈比最大值,但是你发现其实任意一个\(i\)到\(to_i\)这一段是不可能被别的段包含的,也就是从任意一个点开始走都会走到\(i\)和\(to_i\)之间的一个点,然后就想到其实可以变换起点,只需要把这一段之间的每个点当成起点然后算一下最小值就行了,用鸽巢原理可以发现最小的那一段的长度肯定小于等于\(\frac{n}{ans}\),每次找一遍值的时间可以近似成\(O(ans)\),时间就对了。一定要学会简化冗余的枚举,要尝试通过归纳来寻找相似点以找到时间更短的做法。 - Pudding Monsters
这道题之前写过,但是题单里有,所以就又写了一遍。首先把输入改成\(a_x=y\),然后就把二维的限制搞成一维的了,然后就能发现合法区间满足\(max-min=r-l\),然后就是新东西了,考虑从左到右枚举r,把\(max-min+l-r\)用线段树维护,考虑线段树上的一段[L,R]什么意思,显然意思就是当前的左端点在[L,R]内的最小值及最小值个数。每次直接查询区间以枚举到的r为结尾的等于0的个数就行了。考虑每次r右移一位的直接影响,显然就是整个区间都减一,再考虑间接影响,就是\(max\)和\(min\)会改变,那其实只需要更新一下最小值一集最小值的个数就行了。要尽量把多维的限制变少,要尽量把无序的限制变成有序的,这样会更好处理,要善于用数据结构。 - Good Subsegments
发现就是上一题的加强版,考虑直接把询问区间离线下来,按右端点排序,然后就差不多了,但是你现在统计的就不是全局的答案了,而是一段的答案,那也很简单,你就找这一段区间里的就行了。多和别的题的思想联系。
学了道板子,线段树分治。
04-12
要重新拾起日记了。
先写重要的吧。
晚上打AT,不难发现我一打这种时间很短的比赛就会变得很唐,比如今天的C:减一个数之后不加p,D:反复ctrl+z导致后面写的回到前面之后改完忘加了,然后调了好久。幸亏今天没报rated,要不得更紧张(但是今天如果我报了rated的话就能涨好多。。幸亏E题一遍过了,要不然我就真崩溃了。其实仔细一想这些题如果不是考试可能都是不到3min就能出思路,20min左右就能打完的题,但是到了考试就会因为心理原因而变得难了起来,所以其实锻炼的还是心态,要让自己的心态和对于这种思维题的熟练度慢慢涨起来。
白天写了两道线段树优化建图,一道2-SAT,两道单调队列优化dp,一道斜率优化,之前老师说dp是最简单的我还不信,但是其实真的dp就是靠练的,这种类型的做多了就是很好就能盯出来,勤能补拙吧。
还有就是数据结构还得多练,总是写不对,不管是小的还是大的,总会有几个不管是边界问题还是代码问题的小错误,多改。
要记的是有哪些你感觉比较巧妙的题或者比较难的题和你一天的感受,自己的不足。
- ABC401E Reachable Set
比较好想,肯定要枚举k,然后发现上一个k会对下一个有影响,具体就是:先记录一个答案,从上一个答案转移到下一个之后,如果这个点在之前要被删掉,那答案先减一,很显然,因为他现在不被删了,然后考虑这个点的贡献,那就是它能遍历到的所有之前没被遍历到的大于它的点,这些都是能暴力求的,复杂度是均摊\(O(m)\),然后考虑怎么判断无解,发现其实也不难,只需要再维护一个并查集,在每个点加入的时候遍历它连接的边,找出连接比他小的点的边然后判断1 ~ k是不是在同一个块内就行了,值得注意的是,并不需要每次判断1 ~ k,可以记录一个指针,记录上次到哪里就不在一个块内了,下次就直接加完边之后从这里开始判断就行了,复杂度也是均摊的,还有一个值得注意的点,就是就算这个点无解也要进行上面的计算答案操作,因为它在后面是一直在要求的那块里的。 - ABC401F Add One Edge 3
直径的题一般都挺像的,你只要知道关于直径的一些结论就很好做了。看到题首先想到一个结论:以一个点为根的这颗树的最大深度就是两个直径的深度中的最大的那个。然后你发现如果固定了\(i\)和\(j\)那你其实就能\(O(1)\)算出答案了,就是\(max(max(d1,d2),fz_i+fd_j+1)\)期中\(d1,d2\)是两棵树的直径,\(fz_i,fd_j\)是第一/二棵树中以i/j为根的最大深度,显然这两个数组是可以做到O(n)求出的,先找到树的直径的两个端点,然后以两个端点为根扫一边树并记录下来每个点的深度,最后取最大值就行了。然后你发现虽然这样了,但是复杂度是\(O(n^2)\)的,因为你要枚举两棵树的每个端点来计算答案,于是开始想怎么优化,就发现其实很好做,因为顺序并不影响,你可以先对两个数组都排个序,然后你遍历第一个数组,发现\(fz_i+fz_j+1>max(d1,d2)\)这个式子,对于i递增的时候j是单调不增的,那就很好做了,直接一个双指针找到对于当前的i对应的最小的j就行了然后答案就很好计算了,对于这个i,\(fd_j\) ~ \(fd_m\)这一段是要加到答案里去的,所以你对于\(fd\)数组做一个前缀和,然后直接加就行了,至于\(fz_i+1\),\(max(d1,d2)\)都要计算几次就都很简单了 - ABC401G Push Simultaneously
一眼二分答案题,你先处理出来每个点对的距离,然后直接按距离排序,二分一个答案,然后判断是否合法,判断的条件也比较简单,主要是要看能不能每个人都匹配上一个按钮,考虑到n很小,我们每次可以二分到边的边界之后直接暴力加边,然后进行二分图匹配。
04-20
做了一下昨天因为模拟考而没打的ABC,感觉难度正常,还不错。
- ABC402E Payment Required
这数据范围和这个题面一眼就是让状压的,因为每个问题之间没有关联,所以就状压,然后考虑一个dp数组\(f_{i,j}\),表示选择的集合i,当前还剩的钱j,这里有一个小tip,如果你考虑从当前位置怎么转移的话那你发现自己还可以转移到自己就无限循环了,所以考虑怎么转移到当前位置,那显然就是自己没做对+别的选自己,到这里思路就很明显了,三层循环,一层是之前都做了哪些题,一层是现在还剩多少钱,一层是枚举哪些点可以转移过来,就做完了。 - ABC402F Path to Integer
感觉比E简单,你发现一个位置你如果选他的话那对答案的贡献是一定的,那就是\(a_{i,j} * 10^{2 * n - i - j}\),然后我们就成功的把按位做变成了加法,然后发现这个数据范围和这个\(2*n - 1\)很有搞头,你发现你是可以爆搜n个数的,然后就想到折半搜索,就做完了。
5-1集训
很多考试,很难,也是参加的第一个NOI培训,也是很难。
第一天的考试拿了30pts,至今也只改了T1,太难了。
第二天考试拿了145pts,其实应该是170的,但是题目的数据范围给错了以至于调不出来,改数组大小就过了T1是原,T2的70pts是状压的分+部分分,说实话不太难,但是正解确实没敢挑战,正解是dp,其实不太简单,但是也没想象中的那么难,感觉是前三天最简单的场了,145只能拿10名。
第三天考试拿了40pts,T2没调出来,结果是自己想假了哈哈哈,以后再也不胡乱挑战T2了,好好打点部分分然后去刚T1就行了。
第四天上午讲的贪心,讲的是啥??掉线了好久。。。下午讲的dp还好点,晚上做了三道题,一个是俩dp缝起来,一个判断是否可行,一个全局dp,第一次见俩dp缝一块的。一个是无敌凸性题,当你实在做不出来的时候就直接猜凸性,然后就会发现真的有。一个是一道比较水的状压,比较好想但是有点难写,就当练手了。
后面是三天考试,之后有时间把考试的全补上。
想了很久还是想把考试的改过的题都写一下。
- 机器人大师

你发现最小化不如最大化好做,所以转换成最大化关门时间,然后其实就是分讨。 - 出发 - 出发 :前面是人那人就能关门,那就等价于在前面那个人的点权上加a
- 返回 - 返回 :后面是人那前面的就能关门,那就等价于在后面那个人的点权加上a
- 出发 - 返回 :如果都是人就不用管了,要不然就在俩的边上加a,如果这是同一个人的就得在点上加了
- 返回 - 出发 :这个都不用想,肯定前面的要关门,就等价于前面点权加a
然后你就dp就行了,求一个点集使其中的点权+边权最大,直接dp就行了,但是空间开不下,要滚动数组。
- 食物链

场切,但是是因为之前写过。。
你先考虑如果 \(k = 0\) 你该咋做,那你直接设一个 \(f_i\) 表示有多少个入度为0的点能到这个点就行了,然后答案就是$$\sum_{out_i = 0}f_i$$
其中 \(out_i\) 表示一个点的出度。
然后你考虑 \(k = 1\) 的时候你咋做,发现你只需要再维护一个 \(g_i\) 表示这个从这个点出发能到达的 \(out_j = 0\) 的点有多少个,然后就是
其中 \(sum\) 是不删边的答案。
然后你考虑 \(k = 2\)的时候咋做,你发现这俩点只可能有俩关系,一个是在同一条链上,一个是不在,显然不在的话他俩是不会有交集的,所以俩分别减就行了,但是如果在的话就得小容斥一下了。我们设 \(x\) 是更靠前的, \(y\)是更靠后的,然后再记一个 \(d_{i,j}\) 表示 \(i\) 到 \(j\) 的方案数,那么答案就是
然后考虑不限制 \(k\) 的咋做,发现你需要延续 \(k = 2\) 的解法,所以你需要拓扑,然后在拓扑的时候向上面一样减去 \(d_{x,y}\) 就行了,你发现 \(k\) 很小,所以可以在外面提前拓扑并且记录一下,然后直接 \(k^2\) 做这个事情就行了。
总复杂度就是 \(O(nm + k^2)\)
- 直径

这个赛时写了70,感觉还可以。
先说一下70的状压做法吧。
直接找到直径,然后你只对于选的边在这个直径上的进行计算,不在直径上的选的边你不计算答案,但是你发现这玩意他的顺序是不一定的,你直接枚举可能会错我不知道会不会错我没有试,所以你就用一个队列更新你的状压到的东西就行了。
然后是满分的做法。
你设 \(f_{i,j,k}\) 表示在直径上选了编号为 \(i\) 到 \(j\) 的边,然后填了 \(k\) 个边,那么转移就是
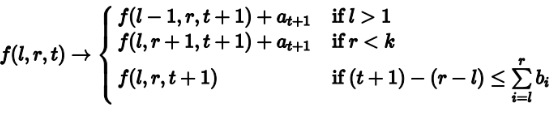
其中 \(b_i\) 表示 \(i\) 连了多少边。
就没了。
- 切题
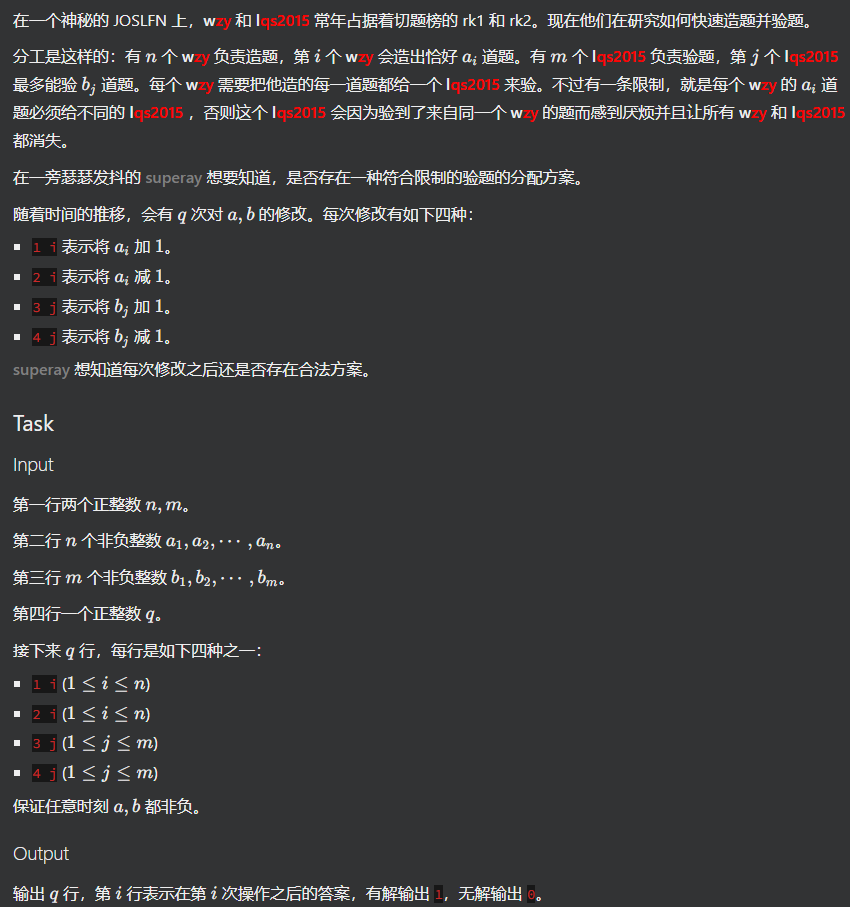
首先有个 \(Gale-Ryser\) 定理,然后你发现合法的条件就是
然后你就对于每个操作,拿线段树维护一下前缀和就行了,值得注意的是,对于 \(b\) 的更改需要特殊注意,因为上面呢个式子要对b进行排序,所以你后面每一步都不能使 \(b\) 无序,所以你要每次更改值的时候找到和要更改的值相同的一段的两端,再根据具体是加操作还是减操作确认是左端还是右端,然后在序列上和线段树上更改。
- 单身狗的复仇

首先先转化题意,就是从这个序列里找到一个上升的连续段,并且任意两个点 \(i\), \(j\) 之前不能存在一个 \(k\), 使得 \(a_i < a_k < a_j\),首先可以想到一个 \(O(n^2)\) 的 \(dp\), 考虑优化,题目要求的是某一时刻所有前缀最小值的不可差分信息,于是使用单侧递归线段树维护。
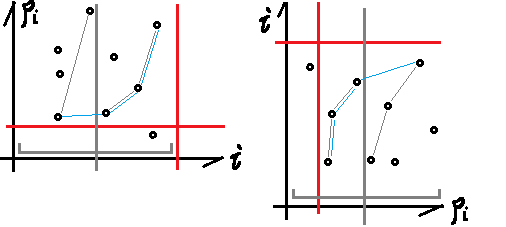
\(i\) 很不好维护,所以维护 \(p_i\),然后就用扫描线之类的做一下就行了。
- 智慧树

首先能想到一个 \(O(n^2)\) 的 \(dp\), 对于每个点记录当前的子树的颜色出现最大值和一共出现的点,然后挨个转移就行了,
因为是子树上的问题,所以可以用启发式合并,然后你就会以为做完了,但是其实不然,因为你需要记录最大值,所以你要开 \(map\), 然后你还要转移,所以要用 \(vector\),而且是对于每个节点都要开,所以你会 \(MLE\), 但是你直接滚动 \(vector\) 就行了。
- 四元组

好题,原是P9850
为了改这道题我还去学了无向图三元环计数和四元环计数。
正向不好做,所以容斥掉蓝色子图,直接算红色子图就行了,直接算不容易,所以可以反演, \(g_i\) 为恰好有 \(i\) 条是红的, \(f_i\) 是至少有,然后考虑怎么算答案,发现就是 \(g_0-g_6 = f_0-f_1+f_2-f_3+f_4-f_5\),然后考虑怎么计算 \(f\)数组。

然后你写一个三元环计数和四元环计数就行了。
- 树

考试的时候看错题了,对着错误题面和样例玩了3h也不知道咋出来的,最后感觉是题出错了去看了一下题,才知道是自己读错题了。。
就顺着我赛时思路写吧。
首先先手玩几个单调的数据,然后发现不管你用什么顺序,最后的操作数总是相同的,然后你思考能不能推广到一般形式,发现显然可以,因为这个是每个单调的组合起来的,你把一段处理出来之后发现又称单调的了,所以就行了,所以现在变成了模拟题,直接做肯定是 \(O(n^2)\) 的,然后你可以线段树上二分之类的优化到 \(O(nlog)\), 但是这样仍然过不了,因为数据时 \(1e7\) 的,所以要 \(O(n)\), 不难想到把一段相同的合并成一段,然后你从后往前扫的时候每次最多分割两个,所以均摊是 \(O(n)\) 的,然后就做完了。
- 游戏

不难发现那个 \(n^i\) 就是唬人的,因为你不可能在不取模的情况下算出来这玩意,所以仔细一想这玩意其实就是个n进制,所以这个题就是让你最大化倒过来的字典序。

05-21
学习了平衡树的衍生的东西,学了fhq-treap,并且把很多板子都用fhq-treap重新写了一边
05-25
把最近几天写的题都总结一遍吧。
- A Simple Task
看数据范围,发现应该是状压,所以很容易就想到一个dp:\(f_{i,j}\) 表示选的点集是 \(i\),现在在点 \(j\),这里钦定从 \(i\) 里最小的点开始的,那么符合答案的状态就是 \(k=lowbit(i)\),其中 \(k\) 是j能到的下一个点。 - 采花
不难发现在一段区间里,只会有个数大于等于两个的有贡献,那我们不妨就钦定第二个是有贡献的。考虑将询问离线,按 \(l\) 排序,然后每次移动 \(l\) 的时候就计算删掉 \(l\) 的贡献,具体就是如果它的后面还有至少两个相同颜色的就不管。统计答案用树状数组。 - 庆典
你发现这个题的性质就是你把它缩点之后把能符合要求的三条边简化掉一条,那不就是树吗,所以直接考虑在树上怎么做。
先考虑 \(k=0\) 的情况,那就是计算出来 \(s\) 在图上能到的点和 \(t\) 在反图上能到的点取交集
那么对于额外加边的询问呢?假设加的一条边为 \(u→v\),如果 \(u\) 在起点的子树内,那么 \(v\) 所在的子树也可以从起点到达,也就是说,起点可达的范围可能会变成不包含的两棵子树。反过来对于终点,如果 \(v\) 在终点到根的路径上,那么点 \(u\) 到根的路径也会变为终点可达的范围,最终就有两条路径的范围。然后直接暴力计算就行了。 - NOIP2015 充满了希望
你发现对于一个询问,能影响的只有最近一次覆盖它的操作和最近一次交换操作,所以你直接用线段树记录一下这个就行了,然后对于每个区间的询问,直接离线按 \(r\) 排序然后直接做就行了。 - 天天爱射击
整体二分 - Sums of Sliding Window Maximum
有一个比较显然的思路是,对于每个数,可以先用单调栈计算出左边第一个大于它的数的下标和右边的,然后你对于每个点的左右计算出的边界端点一个个枚举,算出区间长度并相加,但是这样会错,因为如果有两个比较大的且值相同的,他们会重复计算,所以我们把任意一个的边界定义为大于等于而不是大于就行了。
现在考虑怎么优化。发现可以只枚举 \(L_i\) ~ \(i\),和 \(i\) ~ \(R_i\)中长度较小的,然后差分另一边,这就是启发式分裂,复杂度被证明为 \(O(n\log n)\) 就做完了。 - 寻宝游戏
通过手摸,不难发现答案的计算方式:
设把关键点按照dfn序排序后的数组为 \(a_1...a_k\),然后答案就是 \(2(dis(a_1,a_2)+dis(a_2,a_3)...+dis(a_{k-1}, a_k))\),然后就很简单了,你考虑加一个点的贡献,如果本来就有这个点,那不变,没有的话就在数组里二分出来这个点的左右两个点,答案直接加上 \(dis(x,y)+dis(x,z)-2dis(y,z)\) 其中 \(x\) 是当前点,\(y\) 是第一个小于 \(x\) 的点,\(z\) 是第一个大于 \(x\) 的点,把序列拿 \(set\) 维护一下就行了(第18个自己想出来的紫)。
最大收获是询问要多想离线,多用启发式,多想二分。
05-26
- Sue 的小球
首先能想到 \(O(n^3)\) 的 \(dp\),然后你发现枚举 \(k\) 是多余的,只会从左,右端点转移过来,然后就减掉一维,就没了。 - 二叉查找树
牛牛牛。
这道题最牛的点是你不管怎么变,树的中序遍历的顺序是不会变的,还有就是权值的改变不能有重复的权值,这是很假的,因为能改的数是实数,这一位不行就小数,所以这个是个假的不能重复。
于是就有一个非常显然的区间 \(dp\),\(f_{l,r,k}\) 表示这颗子树的中序遍历的区间是 \(l\) ~ \(r\),里面所有结点的权值都 \(\leq k\),然后我们再枚举一个点作为当前的树的根,再分两种情况(一种是根节点不改变权值,一种是改变权值)直接转移就行了。
最大的收获是在变化中找到不变的东西来维护,还有就是有些东西并不需要在乎形态,有些状态可以多枚举就不用管了,复杂度能对就行了。
05-27
有三道比较显然的蓝,看了就会了,感觉没啥用写的就不写了。
- Pre-Order
其实跟昨天的二叉查找树差不多,也是树的形态和遍历顺序拍成的序列的关系,考虑 \(dp\),设 \(f_{l,r}\) 表示这段内以 \(l\) 为根的方案,你直接枚举下一个和它同级的根,那显然就是要么就是 \(r + 1\),要么就是 \(a_{rt} \leq a_{i+1}\) - Linear Kingdom Races
这题一眼就不是区间 \(dp\),但是可以用区间的思想。设 \(f_i\) 表示考虑到第 \(i\) 条路的答案,有两种转移方案,一个是不选,那就是 \(f_i=f_{i-1}\),另一个是选一段,\(f_i = max_{j=1}^{i-1}f_j+val(j+1,i)-cost(j+1,i)\),其中 \(val(j+1,i)\) 表示把这段的路都选上能对答案造成多大贡献,\(cost(j+1,i)\) 表示把这段的路都选上的代价。然后你发现这玩意可以直接用线段树维护,具体地,对于每个 \(j\),你维护 \(t_j=f_j+val(j+1,i)-cost(j+1,i)\),每次直接按照 \(val\) 和 \(cost\) 的贡献直接区间更改值就行了。
06-01
写了一下昨天的ABC,不出意外的话能写到F,G确实比较偏构造了,没想出来,但是别的题都还是比较简单的。
- Minimum OR Path
不难想到按位贪心,你考虑最先的答案是 \(2^30\),然后从大到小考虑这一位能不能不要,如果可以的话就减去,判断也是简单的,用并查集即可。 - Athletic
你考虑一个数,它连接比它至少小 \(D\) 的数,单向边,然后你发现这个图就是一个 \(DAG\),那么答案就是从每个没有出边的点到每个没有入边的点的长度的最大值,这个玩意暴力求是平方级别的,所以考虑怎么优化。
不难想到每次转移肯定都是从较小的点向比它大的点转移,所以你就直接从最小的点往大遍历,每次只需要用线段树维护一个这个点当前的最大转移值,然后对于每个点的更新,你就在它的合法区间里找最大值并且加一更新它就行了。 - A/B < p/q < C/D
牛题。
对于一组的不等关系,你先尝试把他们的左右两边的分式都变成真分数,然后再取倒数,接着这么干,直到有一个是假分数,一个是真分数,然后这时的答案就是中间的分式等于1,然后你不断向上迭代出原本的答案就行了。
因为 \(p\) 变小时, \(q\) 也会变小,然后答案又满足最优子结构,如果你不满足那肯定会有一组答案时分母比你小,分子比你大,显然无解。
06-03
- 一直在你身旁
发现区间 \(dp\) 的暴力是显然的,然后你发现,\(k\) 向右移动时,\(f_{l,k}\) 单调不减,\(f_{k+1,r}\) 单调不增,然后用单调队列做一下就行了。 - Ciel and Gondolas
首先有一个三次方的 \(dp\),比较好想出来这个是有决策单调性的,既然决策点是有单调性的,那就直接分治优化一下就行了。 - Yet Another Minimization Problem
跟上一道题一样,只是转移不太一样 - 序列分割
首先通过手摸发现分开的顺序没有用,然后就有一个 \(dp\) 了,感觉是个凸包,斜率优化就没了
06-05
- Snuketoon
slope trick模板题 - Making the Grade G
也差不多是个模板题,但是需要判一下单调不降 - 序列 sequence
同上
06-06
- T-Shirts
不难发现对于每个人做的话会很难,所以直接考虑对于每个T恤做,然后你对于T恤都排序,对于大于 \(c\) 的东西都减 \(c\),并且把他们的答案都加一,但是你发现你需要维护T恤的相对大小,然后你发现每次重新减了再排序是肯定不行了,但是你发现顺序的改变只会每次只会把 \(c\) 到 \(2c\) 的点插到小于 \(c\) 的里面,然后你发现你只需要按 \(c\) 排序,复杂度就对了,因为区间慢慢变小,所以这个就是 \(log\) 的了,你还要维护序列,所以要用平衡树,所以最后是俩 \(log\) 的 - Nauuo and Bug
难点在于计算 \(-p\) 次数,所以肯定要改变思路。

用线段树维护即可。 - 对数据结构的爱
和上一道题一样,但是狗屎的是这玩意严重卡常,根本卡不过去,所以你得不用 \(vector\),然后还要把线段树换成指针跳跃少点的玩意,才能过。
06-07
- Zero-Sum Ranges 2
困难计数题。
设 \(f_{i,j,k}\) 表示表示目前加的层里我一共放了 \(i\) 个点,产生了 \(j\) 个区间和为0个区间,有 \(k\) 个间隙

但是前缀和可以是负数,所以你把 \(f_{i,j,k}\) 对应成 \(f_{2n+1-i,m-j,k-1}\) 就成了。 - kangaroo
简单计数题。
抽象一下题意,就是有多少排序,满足头是 \(s\),尾是 \(t\),然后对于 \(i\),要满足 左右都比它小或者左右都比它大。
这不就纯纯是连续段 \(dp\) 吗,考虑加进一个数,可以新开一段,也可以合并两段,都没有啥限制,但是不能加在一段之后,因为这样的话就会一个大于一个小于。
但是新开一段的话需要考虑能不能放在头尾,如果大于 \(s/t\) 的话就不能放,因为这样的话 \(s/t\) 就不能放在端点了。 - Prufer 序列
板子。 - 树的计数
对于树的计数,一般会用到 \(Prufer\) 序列,所以我们要找打这个序列和题目中的 \(d_i\) 的关系
而在 \(Prufer\) 序列中出现 \(d_i-1\)的点在原输入中就是 \(d_i\) 了,然后就是简单计数题了。
06-19
- rsraogps
首先势能分析一下,发现这三个操作都是只会进行 \(O(log)\) 次修改,所以我们只需要记录上次被修改的时间以及值,这样就能做到 \(O(1)\) 查询了。
然后思考一下怎么做这个东西,仔细想想就会发现这个东西肯定要离线做,所以我们先离线下来,按 \(r\) 升序做
当确定一个 \(r\) 时,我们记 \(s_i\) 表示 \(l \leq i\) 时的方案数,然后你差分一下就行了。 - 等差子序列
首先可以发现的是这个题是个诈骗,我们显然只需要找一个长度是3的等差数列就行了。
肯定是枚举三个数里中间的那个。
然后这里就是一个比较套路的东西,你对于值域开一个桶,然后对于枚举过的数就把他们在桶的位置赋成1,然后你就对于枚举的这个数跑一下看看有没有不是回文的串就行了。
如果没有回文的,那就是一个比它小 \(k\) 的在一边,另一个比它大 \(k\) 的在另一边。
判断是不是回文可以用哈希,用线段树维护更新和查找就行了。 - Three Occurrences
把这道题的问题分解成两部分。
一部分是快速查找当前区间的数是不是都只出现了三的倍数次
另一部分是区间里是不是所有数都出现了小于等于三次
对于第一个,直接维护一个哈希数组 \(h_i\),表示 \(1\to i\) 所有数的出现次数%3的哈希值,要注意的是每个不同的数要给他们赋的哈希值是不同的,然后对于一个区间 \([l,r]\),只需要看这两个位置的哈希值是不是一样就行了。
对于第二个限制,我们直接在处理的时候用桶记录每个数的出现次数,如果大于三就左移左端点,直到满足。
不难看出来这两个维护的方式都需要用双指针来做,这里讲一下为什么双指针是对的。
对于一个合法区间 \([l,r]\),当 \(r\) 右移时, \(l\) 是一定不会左移的,所以可以用双指针,而对于每次移动 \(r\),我们都通过移动 \(l\) 保证了这个 \(a_r\) 在区间里出现了小于等于3次,所以每次处理的时候我们只需要管当前的 \(r\) 就行了。 - 轻重边
很好的 \(trick\)
你考虑每次操作就是吧这段书上路径经过的点都赋成一个新的颜色,一段路是重边当且仅当它的两头的端点颜色一样。
然后用树剖维护一下就行了。
06-20
- 括号序列
肯定是个 \(dp\),仔细观察一下,发现是一个大力分讨 \(dp\),因为当前序列的形态有很多种,所以需要根据当前序列的形态来分讨。 - 1.全是 \(*\)
- 2.一个大括号包住里面的东西
- 3.右边是一堆 \(*\),然后左边是合法的任意串,左边以 \((\) 开始
- 4.一堆括号序列和一些 \(*\) 串拼在一起,并且左右边界都是合法括号序列,显然这个包含第二条
- 5.左边是一堆 \(*\),然后右边是合法的任意串,右边以 \()\) 结束
- 6.左,右边都是一堆 \(*\),中间是任意合法序列,显然这个包含第一条
这五个东西都要是合法区间。
然后就是转移了。 - 1.只需要判断区间是否全是 \(* / ?\),以及区间长度是否合法就行了
- 2.只需要判断左右边界是否可以填左右括号就行了,包含的东西可以是1,3,4,5,没有2和6的原因是:2被4包含了,6外面包括号是不合法的
- 3.左边的4情况和右边的1情况拼起来。有人可能会问为什么不能左边的4情况和右边的3情况,因为这个会被4+1的情况包含住
- 4.左边是3,4情况,右边一个括号序列
- 5.左边是5,6情况,右边一个括号序列
- 6.左边5,右边1
这道题就是分讨比较多。 - Turtles
考虑合法的路径肯定是从下出去从左到终点的和从右出去从上到终点的乘积
考虑在这个情况下不合法的是啥,发现其实就是从下出去从上到终点和从右出去和从左到终点的乘积,如果有上面那种但是中间相交了,那我们不妨从最后一次相交的把两个龟走的路径交换,这样就满足上面的限制了。
然后直接计数就行了。
这道题感觉是最简单的。 - 潜入行动
树上分讨背包。
设 \(f_{u,i,0/1,0/1}\) 表示在 \(u\) 点的子树,装了 \(i\) 个器,\(u\) 是否装了器, \(u\) 是否被覆盖。
这个的转移感觉比括号序列简单
首先考虑00的情况,肯定就是由01转移过来的
然后是10,那就是 \(v\) 不选,剩下随便,也就是从00和01转移过来的
然后是01,首先没装,所以 \(v\) 一定被盖了,如果之前 \(u\) 已经被盖了,所以 \(v\) 选不选都行,也就是01和11,如果之前 \(u\) 没被盖,那就只能从11转过来
然后是11,如果之前 \(u\) 是选了但是没被盖,那 \(v\) 一定要选,盖不盖都行,从10和11转移过来,那如果之前 \(u\) 是选了也盖了,那 \(v\) 啥都行,就是00,01,10,11
06-21
上午打比赛了。
- SAO
简述一下题意:有一棵树,每个边有朝向,求这棵树的拓扑序的数量
肯定是 \(dp\),设 \(f_{u,i}\) 表示 \(u\) 在以它为根的子树里的拓扑序为 \(i\) 的方案数。
考虑新加一个 \(u\) 的儿子 \(v\),考虑怎么转移,从 \(f_{u,p1},f_{v,p2}\) 转移到 \(f'_{u,p3}\),限制肯定是 \(p1 \leq p3 \leq p1+p3\)
然后转移就很简单了:\(f'_{u,p3}=f_{u,p1} \times f_{v,p2} \times \binom{p3-1}{p1-1} \times \binom{size_u+size_v-p3}{size_u-p1}\)
转移的意义是在 \(p3-1\) 的现在 \(u\) 之前放 \(p1\) 个点在左边,然后在剩下的里面放子树里剩下的
这个式子是 \(v\) 放在 \(u\) 的拓扑序后面的,还有一个是 \(v\) 在 \(u\) 前面的,转移和上一个差不多,只是 \(p3\) 的范围不一样了而已
你发现这个的复杂度是 \(O(n^3)\) 的,所以还得优化
观察式子,你发现 \(p2\) 只出现了一次,而且不是在组合数,所以你就维护一个前缀和就行了,复杂度就被降成了 \(O(n^2)\) - 一双木棋 chess
挺好玩的一道题
考虑怎么维护当前的状态,如果每一行都状压的话很难维护后面怎么走,而且也不连续,所以另辟蹊径
考虑维护一个界限,是下了的和没下的的界限,从左下角到右上角,1是竖,0是横
然后你发现这个就很好维护了,你维护的这个序列如果有101,那就可以变成011了,然后就好做了,然后你就从11110000转移到00001111就行了
然后考虑怎么转移,当前状态肯定是由(上一个状态 \(+a_{i,j}\) )的最大值或(上一个状态 \(-b_{i,j}\) )的最小值,具体是最大值还是最小值需要看当前是谁该下棋了,只需要看当前下棋的个数的奇偶性就行了
06-22
- Tree Requests
考虑暴力怎么做很简单,就是每次 \(O(n)\) 找,然后判断是不是只有一个字符是奇数的就行了
然后你发现直接 \(dsu \ on \ tree\) 一下就行了。 - Comfortably Numb
你先把每个值直接做前缀和,把区间异或和表示成 \(s_{l-1}\)^\(s_r\)
你又发现每次都会有一个区间最大值,所以你建一个笛卡尔树
在笛卡尔树上直接做的话就是 \(O(n^3)\) 的
然后你每次在一边建 \(01-Trie\),移动另一个子树里的指针,在这边查就行了,复杂度就是 \(O(n^2logV)\)
然后直接启发式合并,对于大的区间建立 \(01-Trie\),小的区间移动指针就行了 - LCA
妙妙题
你发现除了这题肯定要树剖和暴力以外其他啥也不会
这题显然离线扫描线更简单,于是你又考虑到差分
然后就又不会了
你考虑对于 \(1\)~\(r\) 里每个数与 \(z\) 的操作,你发现其实就是从1到 \(i\) 的路径上都 \(+1\),再查询 \(1\) 到 \(z\) 中的路径的权值和就行了。
所以把每个询问挂到 \(l-1\) 和 \(r\) 上,然后扫描线,查询每个点上挂着的查询就行了 - Making Friends P
你把连边顺序排序,然后合并的时候直接启发式合并就行了,维护顺序用 \(set\) 维护一下就行了
06-23
- Tree
这玩意肯定是个点分治,具体地你就维护一下这个点的子树里所有点到这个点的距离,然后排序,双指针枚举+计算答案就行了
但是你会算重,可能它们到这个根的路径会重合,所以你需要容斥一下,只需要在递归到孩子的时候把孩子的初值从0定为 \(-w_i\) 就行了 - 毒蛇越狱 / Snake Escaping
好玩题
你发现三种字符至少有一个出现次数 \(\leq n/3\) 而 \(O(q2^{n/3})\) 是能过的
如果符合条件的是 \(?\),你直接暴力就行了
如果符合条件的是 \(0\),你可以考虑把 \(0\) 变成 \(1\),然后容斥
如果符合条件的是 \(1\),就跟 \(0\) 差不多
后面这俩你需要做高维前/后缀和
好玩的分讨题 - 树上游戏
考虑点分治,对于当前分治中心,统计出它自己出发到分治块内的所有路径对自己答案的贡献,和经过它的路径对当前分治块内点的贡献。自己出发到分治块内的所有路径对自己答案的贡献很好求,现在考虑怎么求经过它的路径对当前分治块内点的贡献。
我们对于当前分治中心的每一个子树分别考虑,令\(cnt_i\)为从分治中心出发的进入其他子树的所有路径中,包含颜色\(i\)的路径条数,\(size\)为除了该子树外当前分治块内所有的点的个数。那么,我们\(dfs\)这棵子树计算贡献,假设当前\(dfs\)到\(x\),首先给\(sum_x\)加上\(\sum cnt_i\),即所有在其他子树中出现的颜色的贡献总和,然后计算\(x\)到分治中心的路径上颜色的贡献。
对于一个出现在分治中心到\(x\)的路径上的颜色\(c\),它对\(X\)的贡献为\(size-cnt_c\),因为\(c\)已经在一些路径上出现,它现在能产生的额外贡献为它原来没有出现的路径条数。所以我们给\(sum_x\)还要加上\(size-cnt_c\)。同时\(c\)也会对\(x\)的子树内所有点产生贡献,所以这个贡献要像标记一样往下传递,然后标记一下\(c\)的贡献已经被计算过,往下\(dfs\)时就不用再次计算了。
所以只需要对于当前分治中心求出\(cnt\)数组和每棵子树的\(size\),进入一棵子树时减去子树自己内部对\(cnt\)生的贡献。同时为了防止复杂度退化,我们不能对于所有颜色求\(cnt\),要先统计一下当前分治块内有哪些颜色出现了,这样枚举块内所有颜色的复杂度才是O(分治块大小)。
06-24
- 餐巾计划问题
网络流
如果想到了把一天分成两个点,一个点表示这一天有的脏布,一个点表示这一天的干净布,就会很简单了
原点向左部点连 \(r_i,0\) 的 边,流量是 \(r_i\),费用是 \(0\),表示每一天会获得的脏布,每个左部点 \(i\) 向右部点 \(i+m\) 连 \(r_i,f\) 的边,表示快洗,再向右部点 \(i+n\) 连 r_i,s$ 的边,表示慢洗
还有买新的,就从源点向 \(i\) 连 \(r_i,p\) 的边,再从右部点向汇点连一个 \(inf,0\) 的边,跑费用流就行了 - 家园 / 星际转移问题
判断无解是简单的,用并查集就行。
然后肯定是网络流。然后就不会了
这里有一个很牛的方法,就是枚举答案,然后对于每天就在前一天的残量网络的基础上再加一些东西,再跑最大流,看看是不是流量大于等于 \(k\)
考虑现在怎么在之前的基础上加点和边,肯定是再建 \(n\) 个点,然后和前一天的点连边,你通过这是第几天就能判断哪个点应该连向哪个点了然后还需要跟源点连边,因为也有可能在地球的人上去 - 美好的每一天
就是这个区间只有一个出现奇数次的字母,联想到只有26个字母,可以联想到二进制+异或和
然后区间询问可以通过前缀和来解决
然后你考虑怎么做
很容易想到对于这个区间你可以扫描线一个一个加,然后每次把这个点的前缀异或和加到桶里,查询的时候只需要 \(O(26)\) 就行了,所以就可以直接离线莫队了
06-25
- 数字梯形问题
首先想到网络流
你首先考虑经过这个点时这个点对答案的贡献怎么算,解决方式也很简单,把点拆成两个,连一条 \((x,a_{i,j})\) 的边,具体的流量时多少按照情况定
你发现第三种情况是最好做的,只需要点间连 \((inf,0)\) 的边,因为可以用相同的边,把拆的两个点的流量是 \(inf\),源点向第一行的连 \((1,0)\) 的边,跑费用流就行了
然后你考虑第二种,就是不能走同一个边了,那就把点间连 \(1,0\) 的边就行了
第一种就是把拆的两个点之间连 \(1,0\) 的边就行了 - 最小路径覆盖问题
这道题的第一步我就没想到
第一个问题是求最小覆盖
这个东西可以刻画成初始每个边都在自己的集合,你需要合并尽量多的集合,这个可以这么用最大流做
你先把一个点拆成两个,如果 \(u,v\) 有连边,就把 \(u \to v+n\),然后连 \(s \to i\),\(i+n \to t\) 这样就可以保证了每个点都只对应着一个路径
然后你考虑方案,其实就是你把每个点匹配的来边和它的出边记录,然后直接并查集啥的做一下 - 最长不下降子序列问题
第一问可以用 \(LIS\) 做,然后考虑求方案数
考虑最大流,设 \(f\) 数组是你进行 \(LIS\) 的数组
对于 \(f_i = 1\) 的点,源点向它们连容量为1的边,因为只能从它们开始贡献一种情况,然后对于 \(j>i,a_j \geq a_i,f_j=f_i+1\) 的两个点连容量为1的边,因为在这种情况下 \(i\) 是向 \(j\) 贡献的,然后对于 \(f_j = ans\) 的点,把它们向 \(t\) 连一个容量为1的边,最后跑最大流就行了
对于多次使用的限制,只需要把这两个边处理成 \(inf\) 的流量就行了,注意看看能不能赋成 \(inf\) 的流量 - 最古の遺跡 3
首先考虑 \(dp\),设 \(f_{i,j}\) 表示考虑了后 \(i\) 个,高度阈值为 \(j\) 时的转移方案数,这里的高度阈值的意思是前面没被震掉的点的高度包含了 \(1\) 到 \(j\),这里设 \(c_0\) 是前 \(i-1\) 个数中钦定消失的柱子,\(c_1\) 是钦定存在的
此外,我们需要区分一下同样高度的两个柱子以便转移,最终答案就需要除掉 \(2^n\)
如果这个点钦定 \(i\) 消失,那转移就是 \(f_{i+1,j} \times (j-c_0+1)\) 因为 \(i\) 这个点的选值就要从 \(j\) 个里选,并且减去消失的 \(c_0\) 个
如果是存在的,我们同样考虑它的高度


06-27
你不得不承认好好读题很重要,我因为读题少了两个条件而空想了好久
首先有一个三次方的 \(dp\),就是设 \(f_{i,j}\) 表示你考虑到 \(i\) 了, 最大的一位时 \(j\),然后直接转移就行了
你对着这个式子盯了很久,发现根本无法优化,所以考虑正难则反
考虑算出来合法的,然后拿 \(n! - ans\) 算出来不合法的
设 \(f_i\) 表示考虑到 \(i\) 了,且现在还没返回的 \(1 \to i\) 排列数量
转移方程式就比较好推出了
意义就是把 \(i\) 放在第 \(j\) 位上,从之后的 \(i-1\) 个数里选 \(i-j\) 个数放到 \(j\) 后面,且随便放的方案数
有聪明的小朋友就要问了,那前面的 \(j-1\) 个数这样就不是 \(1\to j-1\) 的排列了呀,为什么还能保证正确性呢
其实是因为 虽然不是排列,但是它们是互不相同的,所以计算方法和排列一样,所以算出的答案就是\(f_{j-1}\)
上面加粗的这句话很重要,可以说是做这道题的关键。
我们现在就有了一个平方级别的式子,考虑怎么优化
在任何方向的优化都无果之后,你考虑对组合数下手,即拆开式子看看有没有什么性质
然后上下就可以约掉了,然后那个 \(\frac{(i-1)!}{(j-1)!}\) 里的 \((i-1)!\) 就可以提出来了
所以现在的式子就是
你把 \(j-1\) 变成 \(j\)
我们设 \(g_i=\frac{f_i}{i!}\),然后我们就会发现其实 \(f\) 是 \(g\) 的一个前缀和状物,所以直接前缀和优化一下就行了
值得注意的是,你把 \(g\) 数组单独算,然后再去更新 \(f\) 数组的话是错的,但是我不知道是为啥,我觉得可能是没有联系实际意义啥的,有知道的大佬求教一下
然后就是求答案环节了, \(ans=n!-res\)
就是枚举 \(n\) 在哪个点,然后前面是啥,后面随便放的方案数,这个就包含了所有返回的是 \(n\) 的情况 (包括提前返回的和最后返回的)
这个题的式子太妙了,我想一万年也想不出来
有了之前几天的做题经验,肯定会想到先通过最大值建立笛卡尔树,在这个上面做东西
然后你考虑启发式合并,就是在区间较小的儿子里移动指针 \(i\),再在区间比较大的儿子的某个数据结构里查 $ \leq a_u-a_i$ 的到底有几个
最直观的数据结构肯定是权值树状数组,但是你发现你并不想每个点都开一个,所以你考虑只维护一个,然后对于在区间 \([l,r]\) 里查询小于等于 \(x\) 的数的个数这一操作,你把它差分一下,先让答案减去 \([1, l-1]\) 的查询,再在树状数组上加上 \([l,r]\) 的贡献,再让答案加上 \([1,r]\) 的查询
今天虽然写的题不多,但是收获还是不小的
首先就是一定要多想正难则反,排列的本质其实就是一堆不相等的数,然后就是要多用差分,我写这道题的时候没想到差分写了半天,最后看到题解是差分,瞬间可以少写很多,而且不差分的话我的复杂度貌似是错的
06-30
这几天学习了 \(SAM\) 和 \(SA\),并且写了几道题
这道题其实就是要求你在 \(SAM\) 上每次加点的时候统计当前字符串的本质不同子串个数
首先答案是累加的,也就是 \(ans_i=ans_{i-1}+x\),现在考虑加的是啥,你发现其实就是新加这个点之后多出来的子串,那就是这个点的 \(endpos\) 长度,所以 \(x=len_i-len_{fa_i}\)
本题让我们求本质相同和不同的字典序第 \(k\) 大的子串
首先考虑本质不同的,就是在 \(Parent\) 树上把每个点的贡献都赋成1,然后在 \(DAG\) 图上跑一遍后缀和就行了
然后考虑本质相同的,那就是在 \(Parent\) 树上把每个点的贡献赋成它在原串上出现的次数,也就是它子树的贡献和,然后在 \(DAG\) 图上跑后缀和
这道题要求的东西有点混乱,所以整理一下要求的东西
1.求出所有出现次数为 \(k\) 次的段
2.把这些段的抽象成它们的长度
3.求出出现次数最多的长度(次数相同,输出长度更大的)
第一个显然可以想到 \(SAM\),出现次数 \(k\) 次的点就是 \(endpos\) 为 \(k\) 的,在 \(Parent\) 树上统计子树贡献和就行了,然后考虑对于一个满足1要求的点怎么处理
你发现这个点对应的是一段连续的满足要求的长度,所以可以直接差分
差分之后你就枚举就行了
如果是一个串的话就很好求了
但是它让求的是循环同构,所以比较困难
我们考虑把这个串复制一遍到后面,然后在 \(SAM\) 上跑,如果匹配的长度等于 \(len\) 了就说明匹配到了
具体来说,如果匹配到大于的,就跳 \(father\) 边直到长度等于 \(len\) 了,如果后面那个没匹配了,也是跳 \(father\) 边直到后面能匹配,然后更新长度
不难发现这是对的,因为你的匹配的左端点每次如果能匹配一定会先匹配到
这俩是弦论的两种情况分开的题
如果只有两个的话该怎么做?
对于小的建 \(SAM\),然后拿大的在小的上面直接跑就行了
如果有很多呢
你考虑借鉴两个的做法
对于每个串,你在第一个串建的 \(SAM\) 上面跑,到了每个点你都记录这两个串在这个点能匹配到的最大长度
然后你考虑多个串的时候,发现就是把这个点每次能匹配到的最大长度取 \(\min\) 就行了
题解用了很长的代码写了一个没用的东西
07-01
对于第一个串建 \(SAM\)
然后每个串在原串的 \(DAG\) 上跑,什么时候没有那个出边了,那个就是答案
这道题是看得出来用 \(SA\) 很好做
比较显然的想法是先把字符串复制一遍
后面就呼之欲出了,你直接对复制了之后的东西做 \(SA\),然后从小向大扫,如果这个长度大于 \(n\),那就输出最后一位
不难发现哪边小就把哪边放到前面,这显然是最优的
考虑如果俩一样怎么办,不难发现只需要哈希一下看到从两边正序/倒序哪个更小就放哪个就行了
乍一看没啥思路,其实很简单
因为要求的是两个序列只要一个序列里所有点同时+/-一个数和另一个序列相等就行了,所以我们考虑把 \(a_i\) 变成 \(a_i-a_{i+1}\)
然后直接在一个串上建 \(SAM\),把别的串在这个上面跑最大子串匹配,然后记录 \(mx\),\(mn\) 数组并且就行了
值得注意的是,答案是最大匹配 \(+1\),因为你是差分的,所以答案序列会多1,还有就是可能会减成负数,所以要集体加一个大数
艰难计数
我们考虑把它转化成网格,由于我不想画图,所以这里直接上截图
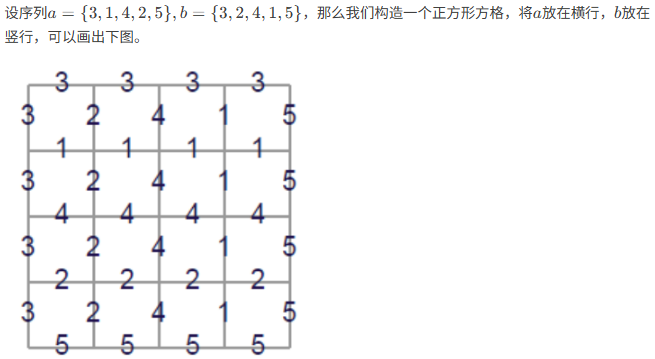
我们设 \(f_{i,j}\) 表示走到了 \((i,j)\) 的方案数,考虑怎么求
其中 \(C\) 是卡特兰数
解释一下这个式子,就是从左或上两个格子转移过来再减去不合法的
考虑什么时候会被减,首先肯定要满足 \(a_i=b_j\) 才行,然后就是以 \((i,j)\) 为右下角的正方形里的向左上的对角线上某些点,这些点的行和列值是相同的,所以这个时候沿着这个矩形直接走到 \((i,j)\) 就会算重
如果这种点只有一个,那肯定就减一了,但是如果有很多这种点的化,就需要卡特兰数了
使用卡特兰数的原因是我们只会在行和列相同的地方转弯,这样这个值才是相同的,所以就成了有个斜线和若干个点,不能经过斜线的方案数了
然后对于这些点们依次把每个成为开头的情况算一下就行了
07-05
不难发现,环是不可能被删除的,所以我们只需要考虑 \(DAG\) 和一个点在环上的 \(DAG\) 的情况
你先不考虑 \(DAG\),先考虑树的情况
你又发现,如果是树的话,可以分成有根树和无根树,如果是有根树,也就是一个点在环上的,那么那个点一定不会被选,所以选择顺序只能是从下向上的,这个直接做一个背包就行了
如果是无根树,也就是没有点在环上,那根节点是有可能提前被选的,所以是不可以这么做的,根本原因是你不知道根节点是哪个以及你会算重
然后你观察数据范围,发现可以对于这种无根树每个点,分别把它们设成根,然后算一遍,但是这样会算重,你考虑为啥,你发现对于一棵点数为 \(n\) 的树,你考虑了 \(k\) 个点的情况,它的根可能有 \(n-k\) 种,但是根最后只可能有一种,所以要除 \(n-k\),然后你对于每种情况都除一遍就行了
然后你考虑 \(DAG\) 咋办,然后你就发现其实 \(DAG\) 是可以拆成多个树来做的,而且相互之间其实没有联系
肯定是要建 \(SAM\) 的,肯定是要在 \(c\to d\) 这段上查询某些东西
首先想到二分一个答案,然后用倍增找到 \(Parent\) 树上表示 \(c\to c+mid-1\) 的点,然后查询这个点的 \(endpos\) 集合里是否有结尾在 \(a+mid-1\to b\) 的,如果有,那就是包含一段这么长的了,现在考虑怎么查询
考虑一下怎么在 \(Parent\) 树上维护每个点的 \(endpos\) 点所在的位置,每个点都表示一个集合,然后还要向上合并,并且没有修改
所以考虑使用权值线段树+线段树合并,然后做一下就没了
07-05
首先我们知道一个结论,当 \(m > 3n+6\) 时这个图一定不是一个平面图
所以现在 \(n\) 和 \(m\) 同阶了
如果两个线会相交,那我们就把他们调整为一个在里面,一个在外面,也就是把一个线建两个点,然后 \(i\to j',j'\to i,i'\to j,j \to i'\),有的小朋友可能就直接开始写 \(2-SAT\) 了,但是更聪明的小朋友会想到这玩意其实用并查集就能维护,因为俩点会连俩边,所以其本质就是并查集
如果没有 \(x\) 怎么做?
不难发现你就直接对于那些限制连边,然后 \(2-SAT\) 就行了
然后观察到 \(x\) 的个数很少,所以我们直接想到暴力枚举当 \(x=a,b,c\) 的时候序列是否合法
但是你发现这并不能过,然后你就想到其实只需要枚举 \(x=a,b\) 就行了,因为这两种情况就能覆盖 \(x\) 这个位置取 \(a,b,c\) 的情况了
这种题一般都是先求出来一组可行解,然后通过这组可行解来求出来所有的方案
可行解是好求的,用 \(2-SAT\) 即可,然后考虑求出所有解
这里规定冲突点 \(j\) 为:
- \(i\) 是自己人且 \(j\) 是敌人且 \(j\) 是 \(i\) 的朋友
- \(i\) 是敌人且 \(j\) 是自己人且 \(j\) 和 \(i\) 不是朋友
显然只有一个点的冲突点 $ \leq 1$ 时,它才会对答案有别的贡献
如果 \(i\) 和 \(j\) 互为冲突点且它们的冲突点只有对方一个,那答案就会 \(+1\)
然后剩下的贡献就是 \(sum_1 \times sum_2 + sum_1 + sum_2\) 其中 \(sum_1\) 是自己人且没有冲突点的点个数,\(sum_2\) 是敌人且没有冲突点的点个数
不难推出上述式子。
07-06
不难发现 \(f_i\) 是 \(i\) 点到直径两端距离的 \(\max\)
题目让你求的东西有俩限制,你要是硬做会非常困难,所以你考虑怎么消除一个限制
你先考虑哪个点的 \(f_i\) 是最小的,不难发现是直径的中点
然后你通过思考发现如果你把这个点变成根,那么这棵树就满足了 \(f_{fa} \leq f_u\)
这样的话你只要从根向下遍历,以当前点为最大值,就可以二分它的祖先上第一个满足条件的最小值,然后这些点就可以组成一个集合
你考虑怎么统计答案,对于你二分出来的东西,你直接树上差分一下,然后每个点的值就是当它在集合里的时候能有多少个点满足限制,然后你取最大值就行了
07-10
首先考虑怎么确定出来叶子集合和非叶子集合
考虑这种情况,如果两个集合的交集为两个点,那这两个点就一定不是叶子
然后你就把叶子和非叶子确定出来了,并且顺便输出了非叶子之间的连边
然后你现在确定叶子的父亲
我们定义一个连边集合为一个非叶子节点和与它相邻的非叶子节点组成的集合
如果一个叶子节点的集合,去掉所有叶子节点,它的集合如果等于一个连边集合,那它的父亲就是这个连边集合的属于的点
至此,我们就确定了所有节点的连边方式,但是时间复杂度是三次方的,所以我们要开 \(bitset\) 来优化时间复杂度
然后还有一些特殊情况
1.只有两个点:直接输出就行
2.菊花图:直接输出就行
3.只有两个非叶子节点:你会发现这种情况下每个叶子节点都会包含那两个非叶子节点,所以你无法确定它们属于哪个节点,所以你就随便钦定就行,具体地,你先枚举一个叶子节点,再去枚举别的叶子节点,如果这两个叶子节点在同一个集合里,那他俩就是兄弟,反之则不然,然后就能确定了
毫无头绪,然后你发现答案具有可二分性,所以你尝试二分答案,然后把树上每条边都减去这个答案,然后判断树上有没有一条路径满足长度在限制之内且这条路径的值加起来不小于零
这个玩意暴力是简单的,你直接设一个 \(f_{i,j}\) 表示在 \(i\) 为根的子树里长度为 \(j\) 的路径的最大值,然后边更新边算就行了,复杂度是 \(O(n^2logn)\)
但是这个复杂度太错了
但是这个是维护路径的,所以你可以点分治,但是这里其实有一个更加厉害的做法,就是长链剖分
考虑对 \(u\) 的一个子树 \(v\),加进它的时候怎么算答案
你就先枚举 \(v\) 的长链的长度,对于一个长度,你肯定要先算出来以 \(v\) 为根的子树中这个长度的最大值,然后再在 \(u\) 的子树中查两个长度限制减去枚举的长度之间的那些长度的最大值
然后你考虑怎么快速求出来子树中某段长度区间的最大值
肯定是线段树吧,但是怎么维护?
你把一个长链的 \(dfs\) 序变成连续一段的,是不是就能求了,你发现是真的,但是一个子树里会有很多区间,所以区间里到根的长度相同的点有很多,值自然也有很多了,那该怎么维护这些值?
挨个查肯定是不行的,会爆炸,所以我们想到把这段长度相同的值的线段树的值并到长链的那个线段树的值上,然后你每次就在长链上查就行了
这很对啊,而且也非常的好写,你只要每次先处理长链所在的子树就行了,然后把这个子树直接继承给父亲,然后在做别的子树的时候每次就慢慢把别的子树上的值更新到长链上就行了,非常的好写其实也有很多细节
07-12
好题
首先思考如果没有 \(x\) 这个限制该怎么做
可以证明的是,使用 \(k\) 条路径可以覆盖一个叶子有 \(2k\) 的树
要选路径,我们肯定会先选直径,然后以直径的两端分别为根,再去选别的路径
一个比较重要的性质:收益最大路径一定是从叶子开始的
所以我们就从根节点向下更新每个点到根节点的路径长度,然后选 \(2y-1\) (因为根节点也是一个叶子)个叶子就行了(每个叶子都代表它到)根的距离
但是你发现这样会算重,所以考虑使用长链剖分,并记录每个链的开头的点和以它为开头的这条链的长度+它到它父亲的路径长度(因为要联通),你发现这样还是选 \(2y-1\) 条,因为每条链一定包含一个叶子
不难发现前 \(k\) 大的链一定是一个连通块,因为如果有一个更长的链但是不在这个连通块里,那它代表的链一定会向上拓展
所以我们只需要长链剖分并且维护每个链头所代表的链+到父亲的链长,并且取前 \(2y-1\) 个就行了
但是我们并没有考虑到必须包含 \(x\) 的限制
如果前 \(2y-1\) 条路径已经包含了 \(x\),那就不用管了
但是如果没有包含的话我们考虑有哪些方案可以让他包含上
1.比较显然的就是把选了的最小的那个链删了,并且接上x所在的那个链
2.但是其实还有一种情况,就是找到离 \(x\) 最近的那条长链,并且把它改接到 \(x\)
把两种情况分别算一下取最大值就行了
但是其实代码挺难写的,需要维护很多东西
07-14
抽空写了写数位 \(dp\)
设 \(f_i\) 为有 \(i\) 位是 \(1\) 的数字个数,所以答案就是 \(\sum i^{f_i}\)
可以用记搜,设 \(f_{cur,up,tmp,d}\) 表示当前是第 \(cur\) 位,是否顶着上界,当前有几个 \(1\),一共有几个 \(1\),然后直接记搜就行
一个串包含回文串的充要条件就是任意一个位置的前两个位置中没有位置的值是等于它的值
所以我们直接记这个数的前两位都是啥就行了
所以我们记 \(f_{cnt,up,lead,p1,p2}\) 表示在第几位,是否顶上界,是否有前导零,前两个都是啥
不难看出这个题记搜比较好写,但是有细节
\(p1,p2\) 刚开始要赋成 \(-1\),如果截至现在一直顶上界,那就不能记忆化,因为你这一维记录的是不顶上界的
不难发现 \(A\) 图的反图的贡献和 \(A\) 图一样,所以只需要看 \(B\) 到 \(A\) 图和其反图的变换次数谁合法就行了
比较套路了,按截止时间排序,考虑如果当前时间的放不下了怎么办,那就记录一个选的贡献的优先队列,然后从上面取就行了
如果图不连通就是无解
反之就是有解吗,答案是肯定的,你考虑 \(i-1\) 个合法的图加一个点的情况是啥,如果它连的点有染色的,那就不给它染色,所以这一定是有解的
证明有解的方案对我们有很大的启发,我们可以直接对原图给我们建 \(dfs\) 树,然后在这个树上做上述操作就行了
对于这种表格的棋子连通性的构造题我们有一种很经典的套路,就是 \((i,j)\) 赋值成 \((i + j) % 3\),这样可以保证 \(0,1,2\) 中每个数字都不可能连着与自己相同的数字
然后我们又看到要求我们改变的次数 $ \leq \lfloor \frac{k}{3} \rfloor$,联系上面我们构造的表格只有三个数,所以这个看起来像是抽屉原理
考虑构造方案,你发现如果只改一个数,不进操作次数远远不够,而且正确性也很差
所以我们考虑每种情况改两种棋子,且一共有三种情况,且三种情况的操作总次数加起来等于 \(k\)
经过思考可以发现,三种情况可以表示为:
1.将 \(a_{i,j}=0\) 且 \(s_{i,j}=o\) 的变为 \(s_{i,j}=X\),并将 \(a_{i,j}=1\) 且 \(s_{i,j}=X\) 的变为 \(s_{i,j}=o\)
2.将 \(a_{i,j}=1\) 且 \(s_{i,j}=o\) 的变为 \(s_{i,j}=X\),并将 \(a_{i,j}=2\) 且 \(s_{i,j}=X\) 的变为 \(s_{i,j}=o\)
3.将 \(a_{i,j}=2\) 且 \(s_{i,j}=o\) 的变为 \(s_{i,j}=X\),并将 \(a_{i,j}=0\) 且 \(s_{i,j}=X\) 的变为 \(s_{i,j}=o\)
根据鸽巢原理,不难发现至少有一个满足条件
这种关于序列的构造题一般需要递归求解
先考虑弱化版:如果是一个排列的话该怎么做
我们考虑怎么由一个长度为 \(n\) 的序列构造出一个长度为 \(n-1\) 且满足 \(a_n=n\),满足原来的前 \(n-1\) 个数的偏序的序列
我们设 \(pos[a[i]]=i\),也就是表示这个值在原序列上出现的下标
通过观察样例,有一个思路显现:依次交换 \((pos[a[n]+1],n),(pos[a[n]+2],n)...\),不难发现这样是对的,因为这样到最后,不仅最后一位是对的,而且之前的换的每一位相当于 \(-1\) 了,所以相对大小不变
然后我们就解决了排列的情况,然后我们发现我们只需要按照值域为第一关键字,原始下标为第二关键字把原序列转换成排列就行了
有一个非常牛的判断环的东西:你对于这个图先跑出来一个 \(dfs\) 树,然后这个图上除了这些树边就全是返祖边了,也就是说你树形遍历到的东西只要不是树边,那你就找到环了
考虑有了这个性质该怎么做
不难发现如果有 \(k\) 个点且它们中没有环,那就可以用黑白染色构造出来一个合法的方案
如果这 \(k\) 个点有环,那就直接输出就行
所以思路就出来了,你直接随便按照 \(dfs\) 树遍历,然后如果找到环就输出,如果没找到就最后黑白染色一下就行了
07-16
如果摁着子序列想的话估计这道题就做不出来了
我们考虑把子序列加强为子串
这里设 \(p\) 为 \(a\) 的前缀和,\(q\) 为 \(b\) 的前缀和,并且假定 \(p_n < q_n\)
我们对每个 \(p_i\) 记录在 \(q\) 中第一个不比它小的数的下标,以及差值(\(p_0\) 也要算)
不难发现,差值小于 \(n\)
所以我们现在有 \(n+1\) 个差值,且他们都小于 \(n\),根据鸽巢原理,至少有两对 \(l,r\) 所对应的差值是一样的
既然有两对,那不就相当于对原数组做前缀和结果发现两个地方差值一样嘛
跟前缀和类似,那不就是中间这部分相等嘛。所以直接输出这两段就行了
这是什么神秘题。。
又是一道不可能无解的题(虽然我不知道为什么
还是那句话,序列上的题我们考虑递归求解

考虑这张图,不难发现,这么做每次可以减少 \(8\) 个,并且直接就递归下去了,并且这肯定是最优的,因为普通的交换每次最多能匹配两个,而这个 \(4\) 次交换就换了 \(8\) 个了,所以肯定优
但是如果你要处理的到最后不是 \(8\) 的倍数了,那就不能这么做了,所以 \(10,12,14\) 的时候会有别的更优的做法,这个可以通过爆搜找到
然后你会发现还是不对,你就考虑到是那个 \(n=3\) 搞的鬼,你爆搜一下发现确实是这样的,然后就把这个也特判一下就行了
构造题既然是构造题,就是要让你大胆构造,做构造题的重点我觉得应该是大胆,不要那么严谨,想到啥就往上写,很有概率是对的
07-17
很厉害的一道题,有点难调。
首先这是个竞赛图,其次它要对每个点都算最长路径,我们先想如果不考虑输出1路径该怎么做
如果是刚学了竞赛图的一些性质的可以想到先缩点,然后原图就会变成一条链,然后每个点的答案就是它在链上所在的块以及它后面的块大小
然后考虑构造方案
根据每个强连通分量竞赛图都会有一个哈密顿回路,我们只需要找到每个强连通分量的哈密顿回路就可以构造出来方案了。
其实难点是你第一次写找哈密顿路径/回路的代码,所以会有点难调
先求出来最少改几个
通过手玩不难发现,这个图如果缩点之后链长大于2,那它的解一定是1,因为只要把链中的一个点拿出来做翻转,这个图就成一个强连通分量了
然后你考虑所点之后链长等于2的情况
有一个强连通竞赛图的性质是它一定存在 \(3 \to n\) 的环,所以如果它大于3的话那答案也是1了,因为你可以拿出来一个点并且翻转,原强连通分量肯定还是,另一个也会合并过来
但是还有情况是强连通分量大小小于3,这个怎么办,直接爆搜就行
然后计数是简单的,因为可以 \(O(n^2)\) 做,所以对于不爆搜的情况你可以直接枚举每个点判断翻转之后强连通分量是不是1,但是我嫌麻烦写的 \(\lfloor \frac{n^3}{\omega} \rfloor\),也能过
其实这道题的难度在于对于这些情况的合法性的证明
前 \(n\) 种连边 \(u \to v\),后 \(m\) 种连边 \(v \to u\),然后缩点对于每个点判断是否在同一个点里就行了
你发现直接计算的话半连通子图的形态有很多种,不好记,所以考虑简化
发现每个强连通分量都是半联通子图,并且缩点之后每个半联通子图只会是 \(DAG\) 上的一条链
因为如果分叉了,那分叉的两个点无法互相到达
所以直接缩点记录贡献然后 \(DAG\) 上 \(dp\) 就行了
我当时听说直接倒叙枚举点然后 \(dp\) 就行了,但是其实不行,所以还是得记忆化
这个是好题,希望以后可以做到自己想出来这种题
首先边双肯定是割不掉的,所以直接对边双缩点,然后就变成一棵树了
为什么是一棵树?因为题目中说了两点之间互相可达
然后考虑树形 \(dp\),这种东西肯定是对于每个子树都算它贡献的答案
所以我们记 \(f_{u,0/1}\) 表示考虑 \(u\) 这个子树, \(u\) 子树内不放/放军营,如果放军营的话子树内军营必须全都连接 的方案数
\(V_u\) 表示缩点后点双代表的点个数,\(E_u\) 代表边个数
不难想到初始化:\(f_{u,0}=2^{E_u},f_{u,1}=2^{V+u+E_u}-2^{E_u}\)
考虑怎么转移
\(f_{u,0}= \prod 2f_{v,0}\) 是好想到的就是这个边选不选都行
\(f_{u,1}=f_{u,0} \times f_{v,1} + f_{u,1} \times (2f_{v,0} + f_{v,1})\)
这个转移包含两种情况
1.之前都没有建造军营,所以 \(v\) 必须建造一个
2.如果已经造了军营,则 \(v\) 有没有军营都行,并且如果 \(v\) 没有的话跟 \(u\) 是否联通都行
考虑怎么统计答案,对于一个子树 \(u\),答案肯定就是 \(f_{u,1} \times\) 子树外面的边选不选都行的方案数,也就是 \(f_{u,1} \times 2 ^{s_1-s_u-1}\)
其中 \(s_u\) 表示 \(u\) 子树内的边数,最后的-1表示不算父边,因为如果算父边了就会在父边统计的时候算重
这里还有特殊情况就是根节点没有父亲,所以答案直接就是 \(f_{1,1}\)
这道题很难,我觉得难点主要在于细节过多,并且有的小地方还会算重,所以要很细心地分讨
07-18
一般做这种东西都会用到反悔贪心
先把前 \(p\) 个最大的 \(a_i\) 选了,然后在选 \(b_i\) 的时候进行返回贪心
具体地,维护三个堆:
\(s1\) 维护还没被选的 \(a_i\),\(s2\) 维护还没被选的 \(b_i\),\(s3\) 维护选了 \(a_i\) 的 \(b_i-a_i\)
那么现在有两种情况
1.\(s2>s1 + s3\),那直接选一个 \(b_i\) 就行了
2.\(s2 < s1+s3\),那就要进行反悔,这个代表我们要选一个已经被选的 \(a_i\) 替换成 \(b_i\),并且再选一个 \(a_i\),这个时候我们需要在 \(s3\) 的堆里再加上 \(s1\) 的反悔
最后你把 \(s\) 个 \(b_i\) 选完就行了
前两天做的题的直觉告诉我们这个东西要在 \(dfs\) 树上做
考虑第一个的限制什么时候会满足,发现就是你遍历到的点的深度至少为 \(\lceil \frac{dep}{2} \rceil\),所以如果遍历到的情况满足了,那就直接输出就行
题目告诉了我们,如果不满足第一个那就一定满足第二个,所以现在只需要考虑怎么构造就行
不难发现我们只要把深度相同的点成对输出就行了,不难发现这样最多有两条边
原来的限制看起来很难看,所以我们变换一下限制
\(1 \leq i-a_i \leq n\)
然后就是超级无敌神秘东西了
你直接将 \(i\) 向 \(i-a_i\) 连边,然后每个点都只有一个出边,所以这个玩意就成了个内向基环树森林了
所以肯定有环,找到环了就是有解
为什么?考虑如果有环,它满足什么条件
\(\sum i = \sum i - a_i\),不难发现 \(\sum a_i=0\)
就构造出来了
先假设扫到一个星星之后我们已经知道它所在的那些合法矩形,然后该怎么做
肯定是查询这些矩形里消除贡献的星星的价值和,再和当前星星做比较看选哪个就行了
现在就是解决怎么知道那些合法矩形以及怎么求需要消除的贡献和
首先合法矩形可以用并查集维护每个点能覆盖到的它这一行的左右边界,然后
08-13
根号分治
如果 \(k \ge \sqrt n\),那直接暴力就行了
如果 \(k \leq \sqrt n\),那可以通过 \(dp\) 来预处理出来
具体地,设 \(f_{i,j}\) 表示下标为 \(i\),\(k=j\) 的时候的答案,转移就是 \(f_{i,j}=f_{i+j+a_i,j}+1\)
然后你只需要处理 \(0\leq j\leq \sqrt n\) 的就行了
你先把 \(d\) 个不一样的变换成 \(4-d\) 个不一样的,因为一样的是可以用桶算的
题目保证了任意两个不可能一样,而 \(D\) 最大是 \(4\),所以这启示我们直接暴力枚举哪些下标是相等的
然后在那些下标相等的东西的贡献分别算出来
但是会有一些情况多算,比如 \(0001,0002\),你算两个相等的时候,会把这种情况当成有两个相等的,并且算三遍,所以你减掉就行了
一个相等的情况也是一样,减掉就行了
庭哥推荐的题就是好
刚开始想的是枚举 \(\min\),但是很难做,所以转换为枚举中位数。记为 \(x\)
然后很套路的东西就是把 \(\ge x\) 的变为 \(1\),把 \(< x\) 的变为 \(-1\),然后合法的区间就是区间和 \(=0\) 的
但是你又发现其实区间和 \(>0\) 的也可以,因为这个时候虽然中位数不是 \(x\),但是真正的中位数一定 \(>x\),所以你用 \(x\) 来更新也是合法的,并且这样的话其实相当于限制减少了,会更好算
然后你发现其实还是压不下去时间,根本原因是你需要确定最小值,但是这根本就很不可能
所以你就想到了直接去枚举最小值的位置,然后去看这个最小值属不属于一个合法区间就行了
你重新考虑合法区间的限制是啥,其实就是 \(s_r \ge s_l,l\leq i\leq r\)
你既然要尽量满足这个限制,就一定要最大化 \(s_r\),最小化 \(s_l\),所以你预处理前缀和的前缀 \(\min\) 和前缀和的后缀 \(\max\),判断合法就行了
但是有一些细节,就是你要把前缀 \(\min\) 和 \(0\) 取 \(\min\),因为这代表直接取 \(1\to i\)
08-15
不难发现其实两方是一个在左下,一个在右上,然后中间有个分界线,分界线的拐点必须要放洒水器,然后别的地方放不放都行
假设总功能放的格子为 \(S\),在分界线上放的洒水器有 \(k\) 个,那剩下的方案就是 \(2^{S-k}\)
后面就要 \(dp\) 了,而这个分界线状态比较少,且很关键,所以不难想到按照分界线来 \(dp\)
而转折的话就要记录上一个的分界线方向和现在这个的方向,而分界线只可能向下或者向右走
所以考虑设 \(f_{i,j,0/1}\) 表示现在在 \((i,j)\),且其是在分界线上的点,且这条边是向右/下走的
注意,这个 \((i,j)\) 是格子的边的交点,不是格子
然后就分讨转移是啥就行了
超级无敌诈骗题
当时怎么都想不出来该怎么做,而且因为是一个图,而且选的也不一定联通,所以肯定没法 \(dp\),当时就陷入瓶颈了
然后就想到贪心了,因为最后要做差,这很重要,所以想的是怎么转移边的贡献
然后就开始疯狂尝试,最后发现把边的权值平分到点上是可以的,就对了
证明一下吧,假设是平均分给了它连接的 \(a,b\) 两点
如果两个点分别被两个人选了,那做差就抵消了,如果两个都是一个人选的,那就全加上了
所以就把边权平均加到连个点上,排序之后分别取就行了
来不及了先这样吧


 浙公网安备 33010602011771号
浙公网安备 33010602011771号