2024北京站总结
2024-12-14
今天上午讲了无敌数学,一点都没听懂,但是努力听了一上午,可谓是一无所获。
下午打了洛谷的比赛。
这个感觉没什么好讲的,反正当时考场上唐完了,T2没写出来,破如防。
晚上打了ABC
ABC都很简单,随便写写就过了。
D题也比较简单,双指针直接写就行。
E题也比较简单,优先队列就行,但是要开__int128
还是太菜了,就写到E了,之后应该多打ABC
2024-12-15
今天上午打了THUPC,晚上上课。
THUPC被凯哥带飞了,我写了些J和I但是最后都没写出来,但是凯哥一人连过三题,直接带我飞,加上钊神的J和qjy大佬的M直接位居前四百,我是最菜的%%%
晚上上课,讲的贪心+构造+博弈,但是还没写题,因为没时间,之后补吧。
2024-12-16
今天上午是省选模拟赛,总体来说打的还行,但是还是太菜了,感觉被所有人吊打。
- T1
题意: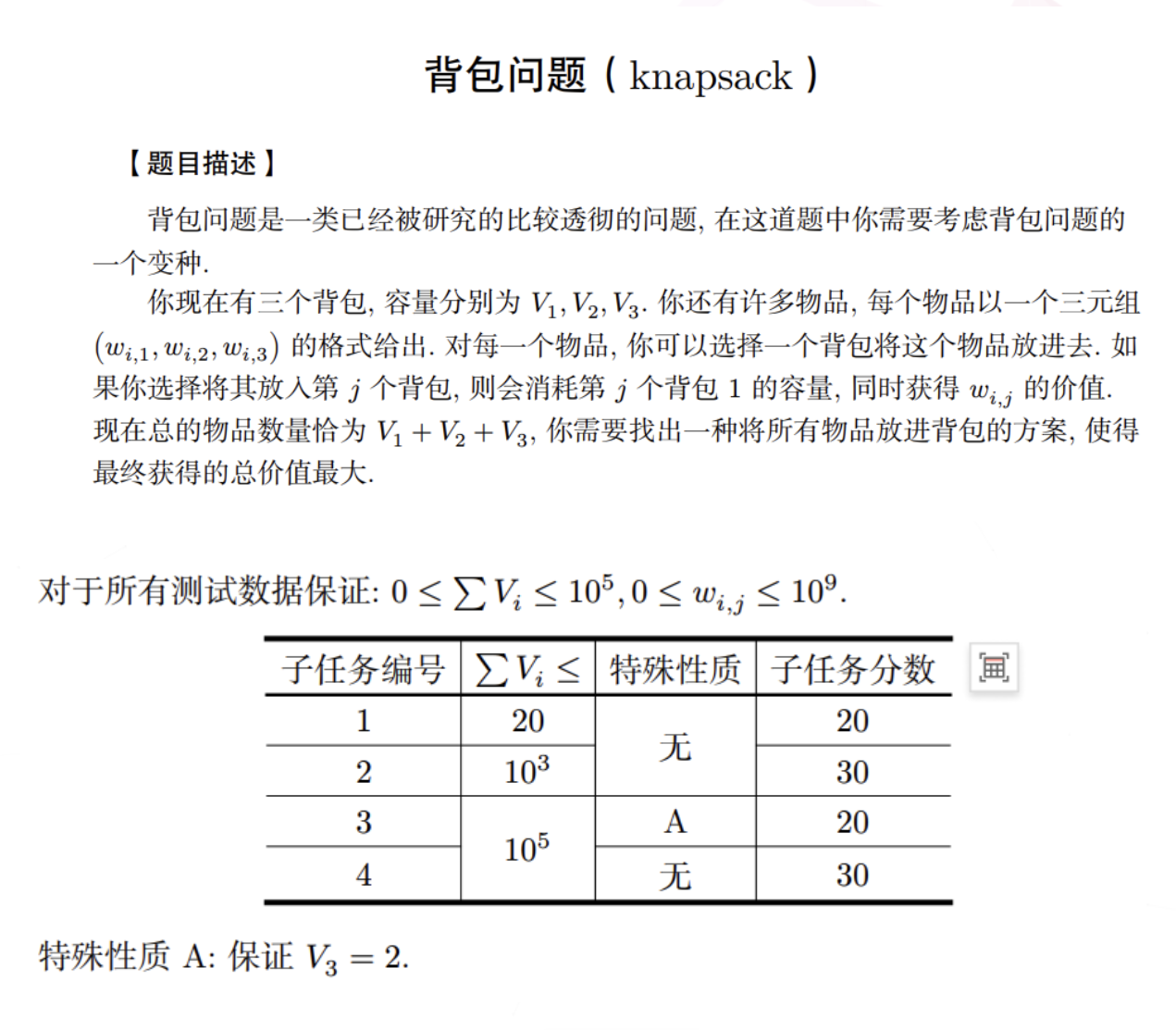
赛时思路:赛时想了差不多一个小时的贪心,后面发现不会贪,当时以为dp是正解,就推了个dp,可以用\(f_{i,j}\)表示第1个背包选了几个,第2个背包选了几个,然后发现转移方程就是\(f_{i, j} = max(f_{i-1,j}+a_{now,1},f_{i,j-1}+a_{now,2},f_{i,j}+a_{now,3})\),能拿50pts,然后想了很久感觉应该有个优化就能过了,但是死活不会,赛后看题解发现还真有这么写的,是用的wqs二分优化过的,但是我太菜了不会。正解是无敌贪心。
正解:首先把所有都放到第一个背包里,然后考虑把v2个放到第二个背包,v3个放到第三个背包。先设\(e_i\)表示\(b_i - a_i\),\(f_i\)表示\(c_i-a_i\),那放到第二个背包的收益就是\(e_i\),第三个就是\(f_i\),然后我们设第i个放到第二个背包,第j个放到第三个背包,考虑什么时候把它俩交换会更优,显然是\(e_i+f_j<e_j+f_i\),移相得到\(e_i-e_j<f_i-f_j\),所以我们就以这个排序,那么放到第二个背包的一定会全在放到第三个背包的前面,考虑怎么获得答案,发现可以用小根堆来处理出来前缀的前v2大的和,后缀前v3大的和,然后就直接枚举断点,找最大答案就行了。
代码:
#include <algorithm>
#include <iostream>
#include <queue>
using namespace std;
typedef long long ll;
const int N = 1e5 + 10;
int v1, v2, v3, n;
ll mx, ans = -1e9;
ll sum[N], pre[N];
struct zx { int a, b, c, e, f; } a[N];
priority_queue <int, vector<int>, greater<int>> q1, q2;
bool cmp (zx a, zx b) {
return a.e - a.f > b.e - b.f;
}
int main () {
cin >> v1 >> v2 >> v3;
n = v1 + v2 + v3;
for(int i = 1; i <= n; ++i) {
cin >> a[i].a >> a[i].b >> a[i].c;
a[i].e = a[i].b - a[i].a, a[i].f = a[i].c - a[i].a;
mx += a[i].a;
}
sort(a + 1, a + n + 1, cmp);
for(int i = 1; i <= n; ++i) {
q1.push(a[i].e);
sum[i] = sum[i - 1] + a[i].e;
if(i > v2) {
sum[i] = sum[i - 1] + a[i].e - q1.top();
q1.pop();
}
}
for(int i = n; i >= 1; --i) {
q2.push(a[i].f);
pre[i] = pre[i + 1] + a[i].f;
if(i <= n - v3) {
pre[i] = pre[i + 1] + a[i].f - q2.top();
q2.pop();
}
}
for(int i = v2; i <= n - v3; ++i)
ans = max(ans, mx + sum[i] + pre[i + 1]);
cout << ans << endl;
return 0;
}
- T2
题面:

赛时思路:不难发现可以直接用0,1表示胜负,然后如果这个点能到的后k个点有必败态,那这个点就是必胜态,但是又注意到还有二操作,所以如果后继全是必胜态也不慌,我们可以进行二操作,所以不难发现如果后记全是必胜态且\(a_i&1\)的话那当前点还是必胜态,然后就可以直接做了,复杂度有点爆炸,是\(O(qnk)\)的,当时做到这就快交卷了,就没往后想了。
正解:赛时思路都是对的,然后后面的操作发现很像 弹飞绵羊 ,然后就可以分块做了,但是时间有点爆炸,需要注意很多细节还要开O2。
代码:
#include <iostream>
#include <cmath>
const int N = 2e5 + 10;
int n, k, Q, op, l, r, d, size, m;
int a[N], p[N][2], q[N][2];
int L[N], R[N], b[N], tag[N];
void build (int x) {
for(int i = L[x]; i <= R[x]; ++i) {
if(a[i] == 0) q[i][0] = std::max(0, i - k - 1);
else q[i][0] = std::max(i - 1, 0);
if(q[i][0] < L[x]) p[i][0] = i;
else p[i][0] = p[q[i][0]][0];
if(a[i] == 1) q[i][1] = std::max(0, i - k - 1);
else q[i][1] = std::max(i - 1, 0);
if(q[i][1] < L[x]) p[i][1] = i;
else p[i][1] = p[q[i][1]][1];
}
tag[x] = 0;
}
void change (int l, int r) {
if(tag[b[l]]) {
for(int i = L[b[l]]; i <= R[b[r]]; ++i)
a[i] = a[i] ^ 1;
tag[b[l]] = 0;
}
for(int i = l; i <= r; ++i)
a[i] = a[i] ^ 1;
build(b[l]);
}
void modify (int l, int r) {
if(b[l] == b[r]) {
change(l, r);
return;
}
for(int i = b[l] + 1; i < b[r]; ++i)
tag[i] = tag[i] ^ 1;
change(l, R[b[l]]), change(L[b[r]], r);
}
bool query (int s, int t) {
while(b[t] > b[s])
t = p[t][tag[b[t]]], t = q[t][tag[b[t]]];
while(t > s) t = q[t][tag[b[t]]];
if(t == s) return tag[b[t]] ? a[s] ^ 1 : a[s];
else return 1;
}
int read () {
int x = 0;
char ch = getchar();
while (ch < '0' || ch > '9')
ch = getchar();
while (ch >= '0' && ch <= '9') {
x = x * 10 + ch - '0';
ch = getchar();
}
return x;
}
int main () {
n = read(), k = read(), Q = read();
for(int i = 1; i <= n; ++i)
a[i] = read(), a[i] = a[i] & 1;
size = std::max(int(std::sqrt (n * 2)), 1);
for(int i = 1; i <= n; i++)
b[i] = (i - 1) / size + 1;
m = b[n];
for(int i = 1; i <= m; i++) {
L[i] = (i - 1) * size + 1;
R[i] = std::min(n, i * size);
build(i);
}
while(Q--) {
op = read(), l = read(), r = read();
if(op == 1) {
d = read();
if(d & 1) modify(l, r);
} else
std::cout << (query (l, r) ? "Alice\n" : "Bob\n");
}
return 0;
}
- T3
题面: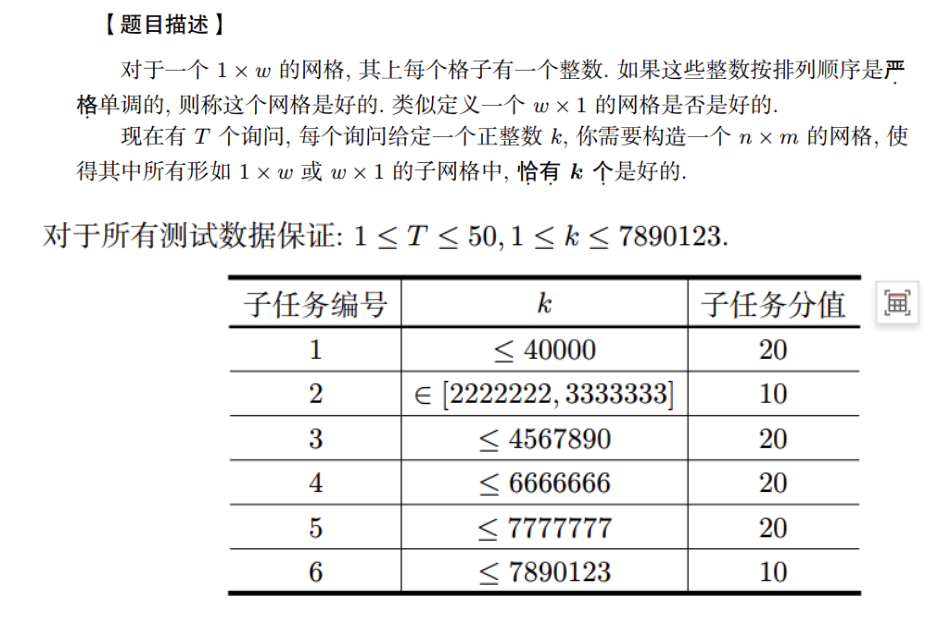
赛时思路:推出来很多东西,当时感觉都很有用,但是真到实现的时候就是不会实现,感觉难受得很,最后也没写对,但是之前也没写过几道构造,能推成这样已经很不错了。
正解:
题解:还没写出来。
2024-12-17
考试。
- T1
题面

赛时思路:考场上就写了写\(a_i=1\)和\(n=1,n=2\)的,别的就不会了,想了很久但是不会,赛后发现写出来的都是打表,终究还是我太菜了。
正解:

无法更加详细了
代码:
#include <iostream>
using namespace std;
const int N = 110;
int T, n;
int a[N];
void Main () {
cin >> n;
bool f1 = 1;
for(int i = 1; i <= n; ++i) {
cin >> a[i];
if(a[i] != 1) f1 = 0;
}
if(n == 1) return puts("Win"), void();
if(n == 2) {
if(a[1] == 1 || a[2] == 1) puts("Win");
else puts("Lose");
return;
}
if(f1) {
if(n % 3 == 0) puts("Lose");
else puts("Win");
return;
}
int k1 = 0, k2 = 0, k3 = 0;
for(int i = 1; i <= n; ++i) {
if(a[i] == 1) k1++;
else if(a[i] == 2) k2++;
else k3++;
}
if (k1 % 3 == 0) {
if(k2 + k3 == 1) puts("Win");
else puts("Lose");
}
else {
if(k2 + k3 >= 0 && k2 + k3 <= 2 && k3 <= 1 ) puts("Win");
else puts("Lose");
}
}
int main () {
scanf("%d", &T);
while(T--) Main ();
return 0;
}
- T2
题面:

赛时思路:40分很好想,直接处理出来这个串然后递推就行了,然后想了很久的60分,但是不会,太菜了。
正解:记\(f_{u,l,r}\)表示从u到根节点匹配了\(s_l~s_r\)的串的个数,然后这个玩意显然可以\(O(n|S|^2)\)做,这样我们就预处理出来了,然后考虑每次询问,发现这样就可以直接容斥做了,具体地,设当前u到lca一共匹配了1i,然后lca到v匹配了i+1len,我们发现1i可以表示成1j和j+1i,所以我们就可以直接减掉u到lca包含1j的方案数乘lca到1包含j+1~i的方案数,然后就做完了。
代码:
#include <iostream>
#include <cstring>
#include <cstdio>
using namespace std;
const int N = 1e5 + 10;
const int p = 998244353;
int n, q, tot, len;
int head[N], dep[N], f[N], st[N][21];
int fz[N][31][31], fd[N][31][31], S[31], P[31];
char a[N], s[N];
struct Map { int to, nxt; } e[N << 1];
void add (int u, int v) {
e[++tot] = {v, head[u]};
head[u] = tot;
}
int Lca (int u, int v) {
if(dep[u] < dep[v]) swap(u, v);
for(int i = 20; i >= 0; --i)
if(dep[st[u][i]] >= dep[v]) u = st[u][i];
if(u == v) return u;
for(int i = 20; i >= 0; --i)
if(st[u][i] != st[v][i]) u = st[u][i], v = st[v][i];
return st[u][0];
}
void dfs (int u, int fa) {
f[u] = fa, dep[u] = dep[fa] + 1, st[u][0] = fa;
for(int i = 1; i <= 20; ++i)
st[u][i] = st[st[u][i - 1]][i - 1];
for(int i = head[u]; i; i = e[i].nxt) {
int v = e[i].to;
if(v == fa) continue;
dfs(v, u);
}
}
void dfsf (int u, int fa) {
for(int i = 0; i <= len; ++i)
fz[u][i + 1][i] = fd[u][i + 1][i] = 1;
for(int l = 1; l <= len; ++l)
for(int r = l; r <= len; ++r) {
if(a[u] == s[l])
fz[u][l][r] = fz[fa][l + 1][r];
fz[u][l][r] = (fz[u][l][r] + fz[fa][l][r]) % p;
}
for(int l = 1; l <= len; ++l)
for(int r = l; r <= len; ++r) {
if(a[u] == s[r])
fd[u][l][r] = fd[fa][l][r - 1];
fd[u][l][r] = (fd[u][l][r] + fd[fa][l][r]) % p;
}
for(int i = head[u]; i; i = e[i].nxt) {
int v = e[i].to;
if(v == fa) continue;
dfsf(v, u);
}
}
int main () {
scanf("%d%d", &n, &q);
for(int i = 1, u, v; i < n; ++i)
scanf("%d%d", &u, &v), add(u, v), add(v, u);
scanf("%s%s", a + 1, s + 1);
len = strlen(s + 1);
for(int i = 0; i <= len; ++i)
fz[0][i + 1][i] = fd[0][i + 1][i] = 1;
dfs(1, 0), dfsf(1, 0);
int u, v, lca;
while(q--) {
scanf("%d%d", &u, &v);
lca = Lca(u, v);
int ans = 0;
S[0] = P[0] = 1;
for(int i = 1; i <= len; ++i) {
S[i] = fz[u][1][i], P[i] = fd[v][len - i + 1][len];
for(int j = 0; j < i; ++j) {
S[i] = (S[i] + p - 1ll * S[j] * fz[f[lca]][j + 1][i] % p) % p;
P[i] = (P[i] + p - 1ll * P[j] * fd[lca][len - i + 1][len - j] % p) % p;
}
}
for(int i = 0; i <= len; ++i)
ans = (ans + 1ll * S[i] * P[len - i] % p) % p;
cout << ans << endl;
}
return 0;
}
- T3
题意:

赛时思路:就写了个20分的线段树做法,复杂度是\(O(n^2logn)\)
正解:

代码还没写,因为不会。 - T4
题意:

赛时思路:没思路,直接排个序按k一个一个加进去就行了,拿到了暴力分
正解

代码还没写,因为不会。
2024-12-18
上午是lxl大佬讲课,听懂了30%(?
下午和晚上写了些前两天的题,ds题看起来都很难做,所以都还没做,准备后天上午做一下。
- P1484 种树
反悔贪心,考虑维护一个大根堆,每次插入这个值和左右端点,如果反悔的话就是把左右端点选了而不选这个值,显然这个玩意是可以反悔反悔操作的,而且每次都是选择的总量增加1,然后就做完了。 - P3620 [APIO/CTSC2007] 数据备份
和上一题很像,把相邻的两个房子的差值当作上一题的值,然后就跟上一题一样了。 - P4053 [JSOI2007] 建筑抢修
小绿题,先把数组按照\(T2\)排个序,然后维护一个大根堆,这个大根堆记录选的所有点,每次插入\(T1\),然后每次就看放进去当前值行不行,如果行那就直接放,如果不行就考虑删掉大根堆的堆顶再加上这个数更优还是不做任何操作更优。 - [AGC014D] Black and White Tree
这个题比较巧妙,考虑什么时候白点能赢,显然是有节点有大于等于两个叶子节点孩子的时候必胜,所以就考虑如果进行到叶子节点就把当前点和它的父亲节点删掉,这样对整棵树这么做一遍,最后如果剩下了有些单独的节点的话那就是必胜,因为剩下的这些节点肯定就是没有父亲节点跟它匹配,也就是说这个节点的父亲至少有两个“叶子”儿子节点,所以必胜。 - [AGC002E] Candy Piles
显然B会一直往右走,直到走不了,所以我们就处理出来在B走到每列的时候A可以走到的最远值,那么我们处理出来这个之后就可以对于每个石头判断当石子走到这列的时候能走到的最大行数是多少,显然如果大于等于的话那就显然被堵住了,就是在这里可以停止游戏。
2024-12-19
- P2515 [HAOI2010] 软件安装
先缩点,然后是个树形dp,设\(f_{u,i}\)表示为在u这个点,选i大小的物品的最大收益。 - [ARC101E] Ribbons on Tree

2024-12-21
- Fairy
如果一个环的包含的边数是奇数的话那肯定不符合二分图的判断,所以要删掉一个边,偶数之类的就没事,考虑怎么删边,可以用一个差分维护一下,如果这个边的值等于奇环的个数的话那肯定要选,别的就不选,然后就做完了。
2024-12-22
- Giving Awards
发现其实就是给出一张有向图,要求构造一个它的补图的哈密顿路径 ,发现这肯定是有解的,因为肯定不会有两点都有到对方点的情况。发现如果有原图的边u -> v,那要么就是v在u前面输出,要么就是v在u后边至少隔1个点输出(返祖边),所以考虑随便找一个原图的生成树,然后只需要在把u的所有孩子都输出了之后再把自己输出就行了。 - Omkar and Last Floor
考虑dp,设\(f_{l,r}\)表示在第lr列已经填完1之后能获得的最大值,然后发现其实是个区间dp,考虑设$s_{l,r,k}$表示在lr中的且包含k点的区间,显然可以\(O(n^3)\)预处理出来,然后就有状态转移方程式了。\(f_{l,r} = max_{k=l}^r(f_{l,k-1}+f_{k+1,r}+s_{l,r,k})\),最后答案显而易见是\(f_{1,m}\) - P1477 [NOI2008] 假面舞会
如果有环,那最大答案肯定是环的因数,如果有起点和终点相同的两条链,那最大答案肯定是长链减短链的因数,最小答案肯定是最大答案的因数,所以考虑把u->v连一条边长为1的边,v->u连一条边长为-1的边,然后跑图,如果再次经过u了那第二次和第一次经过u的差值就是这个环的长度,而最大答案就是所有环的gcd。 - P2371 [国家集训队] 墨墨的等式
同余最短路差不多板子题。 - P4819 [中山市选] 杀人游戏
发现一个连通块内只要你问了一个人,那这整个连通块就不用问了,而且如果你已经问了n-1个人了,那剩下这一个也就不用问了,所以先考虑缩个点,然后对于每个连通块算问一次,值得注意的是,如果有大小为1的连通块,那次数减一,最后再计算答案就好了。
2024-12-23
- P4630 [APIO2018] 铁人两项
圆方树基本板子题,考虑固定e、f,显然c的个数就是他们中间的边的并集,然后我们考虑变成圆方树,方点的值就是这个点双的大小,圆点就是-1,那么这样就可以统计出来了,然后发现根本不用固定e、f,可以直接考虑边的贡献,然后直接在圆方树上计数就好。
2024-12-24
今天是模拟赛。
- T1
题面:

赛时思路:没学过prufer序列,啥也不会,赛时写了1.5h的dp,感觉挺对了,没想到只能过几个样例,差不多算是宝玲了。
正解:先考虑转到prufer序列上做,后面将k个连通块表示成k个点,然后考虑dp,设\(f_{i,j}\)表示考虑前i个点在prufer序列上占了j个位置的方案数。
\[f_{i,j}=\sum f_{i-1,k}· \binom{j}{k}·s_i^{j-k+1}·(j-k+1)!
\]
表示为前i-1个占了k个位置,然后在i占的j个位置中的方案数第i个连通块中选哪些点的方案数题目中要求的答案统计,然后发现这个显然是\(O(n^3)\)的,然后考虑怎么优化,考虑通过分离j和k来把复杂度消掉一维,考虑把组合数,次幂,阶乘拆开,可以发现能约掉很多东西,最后要求的就是
\[f_{i,j}=j!·s_i^{j+1}·(\sum f_{i-1,k}· \frac{1}{k!·s_i^k}·(j+1)-\sum f_{i-1,k}· \frac{1}{k!·s_i^k}·k)
\]
然后发现这玩意前面和后面可以每次预处理出来,就是求和比较麻烦,但是发现求和这玩意可以直接用前缀和求,然后就可以减掉一维复杂度了。
代码:
#include <iostream>
#include <cstring>
using namespace std;
typedef long long ll;
const int N = 7010;
const ll p = 998244353;
ll n, k;
ll f[N], g[N], h[N];
ll fac[N], ifac[N], S[N], s[N], inv[N];
ll qpow (ll a, ll b) {
ll res = 1;
while(b) {
if(b & 1) res = res * a % p;
b >>= 1, a = a * a % p;
}
return res;
}
void init () {
fac[0] = fac[1] = ifac[0] = ifac[1] = 1;
for(int i = 2; i <= k; ++i) {
fac[i] = fac[i - 1] * i % p,
ifac[i] = ifac[p % i] * (p - p / i) % p;
}
for (int i = 2; i <= k; ++i)
ifac[i] = ifac[i - 1] * ifac[i] % p;
}
int main () {
cin >> n >> k;
for(int i = 1; i <= k; ++i)
cin >> s[i];
init(), f[0] = 1;
for(int i = 1; i <= k; ++i) {
S[0] = inv[0] = 1, S[1] = s[i], inv[1] = qpow(S[1], p - 2);
for(int j = 2; j <= k; ++j)
S[j] = S[j - 1] * s[i] % p, inv[j] = inv[j - 1] * inv[1] % p;
memcpy(g, f, sizeof(g));
for(int j = 0; j <= k; ++j)
g[j] = g[j] * ifac[j] % p * inv[j] % p, h[j] = g[j] * j % p;
for(int j = 1; j <= k; ++j)
g[j] = (g[j] + g[j - 1]) % p, h[j] = (h[j] + h[j - 1]) % p;
for(int j = 0; j <= k; ++j) f[j] = fac[j] * S[j + 1] % p * ((g[j] * (j + 1) % p) + p - h[j]) % p;
}
cout << f[k - 2] << endl;
return 0;
}
- T2
题面:

赛时思路:赛时没思路,因为没看懂题,考试结束之后才知道要求的是在这个串上找一个上升子序列和一个下降子序列,两个不能有交,然后答案是两个长度加起来,求答案的最大值。
正解:设x是下降子序列,y是上升子序列,考虑两种情况。
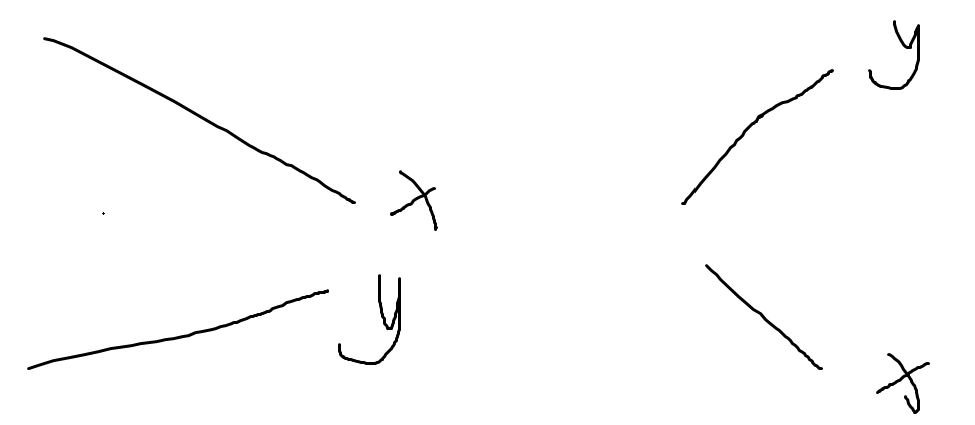
这种情况比较好做,我们可以设\(f_{i,x,y}\)表示考虑到第i个点,下降分到统计前缀最大值的序列里最大的数是x,分到统计前缀最小值序列里的最小的数是y,考虑新加一个点之后怎么做它,显然这玩意是可以转移到\(f_{i+1,a_i,y}\)\(f_{i+1,x,a_i}\),然后就做完了。
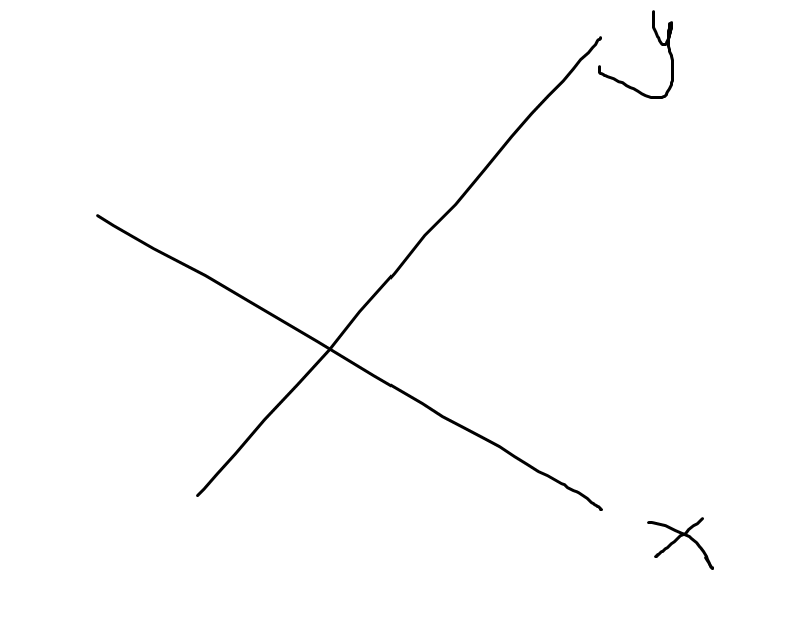
这种情况有点难,我们考虑枚举从哪个点他们开始x在y下面,然后左边我们显然可以直接跟上面一样用dp预处理出来,然后考虑右边怎么做,发现可以用线段树或者树状数组维护右上角那一片的LIS最长值和右下角的LDS最长值,然后直接维护就行了。
代码:
#include <iostream>
#include <cstring>
#include <set>
using namespace std;
const int N = 2e5 + 10;
int T, n;
int a[N], s[N], p[N], f[N], g[N];
int ts[N], tp[N];
set <int> se;
int lb (int x) {
return x & (-x);
}
void adds (int x, int S) {
for(int i = x; i <= n && i; i -= lb(i)) ts[i] = max(ts[i], S);
}
void addp (int x, int S) {
for(int i = x; i <= n && i; i += lb(i)) tp[i] = max(tp[i], S);
}
int querys (int x) {
int mx = 0;
for(int i = x; i <= n && i; i += lb(i)) mx = max(mx, ts[i]);
return mx;
}
int queryp (int x) {
int mx = 0;
for(int i = x; i <= n && i; i -= lb(i)) mx = max(mx, tp[i]);
return mx;
}
void Main () {
cin >> n;
se.insert(0), se.insert(n + 1);
for(int i = 1; i <= n; ++i) {
cin >> a[i];
auto it = se.lower_bound(a[i]);
s[i]= *it, p[i] = *(--it);
f[i] = g[a[i]] = ++g[p[i]], se.insert(a[i]);
}
int ans = 0;
for(int i = n; i; --i) {
ans = max(ans, max(queryp(p[i]) + querys(p[i]), queryp(s[i]) + querys(s[i])) + f[i]);
addp(a[i], queryp(a[i]) + 1);
adds(a[i], querys(a[i]) + 1);
}
cout << ans << endl;
memset(ts, 0x00, sizeof(ts)), memset(tp, 0x00, sizeof(tp));
g[0] = 0, se.clear();
}
int main () {
cin >> T;
while(T--) Main ();
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号