高一上做题记录
放一些做的好题。
图论
-
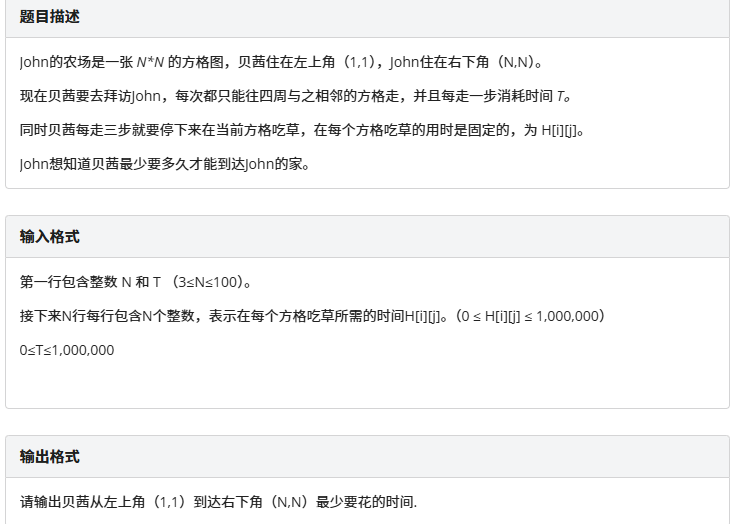
拜访约翰
思路
考虑如果没有停下来吃草的话怎么做,可以想到用最短路,然后考虑有这个限制该怎么做,发现照样这么做,只需要记录一下当前在第几步就行了。 -
输出最短路径

思路
可以直接弗洛伊德处理出来每两点的最短距离,现在考虑怎么记录路径。发现如果两端起点和终点相同的路径它们的代价也相同,那就可以直接找他们的字典序最小值,然后又发现别的情况会直接更新值,而不会更新路径,所以直接再开一个二维数组更新一下就行了。 -
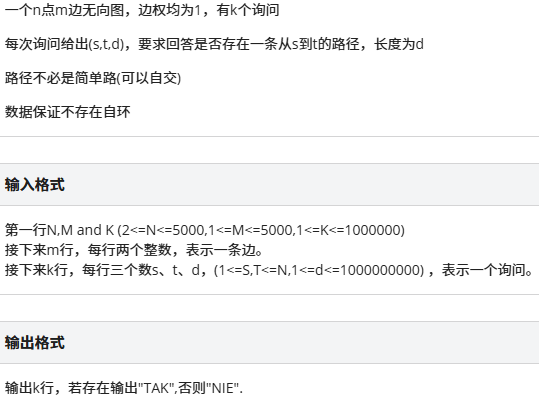
POI2013 Tales of seafaring
思路
首先考虑无解情况,发现如果比最短路小的话那肯定就不可能了,然后发现如果询问的长度是奇数,那它对应的最短路就是奇数的,反之一样,所以我们就直接跑最短路的时候记录每个点的奇数和偶数长度的最短路就行了。值得注意的是,询问次数比较多,会MLE,所以把询问提前记录一下然后做最短路的时候直接更新就行了。 -
公路修建问题

思路
如果确定了最大花费,那肯定选一号公路的数量越多越好,所以如果确定了最大花费,显然可以进行贪心+并查集来检查这个花费是否合法。现在的问题就是怎么找最大花费了,不难想到二分,发现可以。 -
吃草

思路
考虑如果我们知道任意两点之间的最短距离之后该怎么做, 发现可以直接做一个LIS,所以后面就很简单了,先处理出来任意两点的最短距离,然后直接按照点券排个序,LIS找最大值就行了。 -
最优贸易

思路
发现会有一些环,所以先缩个点,然后发现这就是个DAG,发现这个时候只需要贪心就行了,具体地,记录从第一个点到当前点的可以相减的最大值和最小值,发现如果当前点的最大值更大,那就要把最大值和最小值都更新成这个最大值,因为当前点的最大值并不能与之前的点的最小值相减,但是当前点如果更小的话就完全不需要担心,直接更新最小值就行了。
树上问题
-
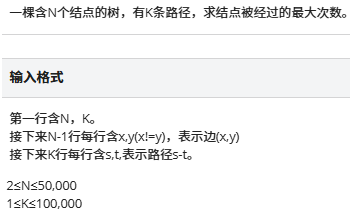
闹市
思路
直接对点进行差分即可 -
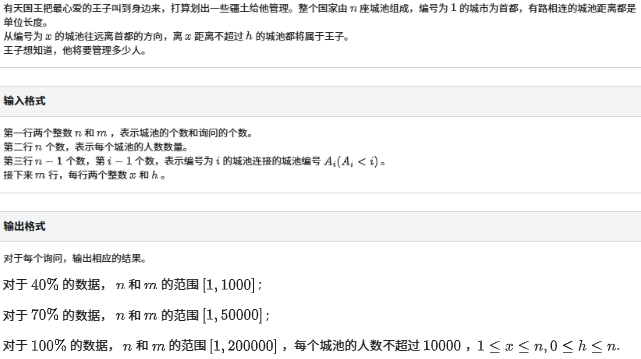
王子
思路
这题感觉有点难,当时没想出来。首先对于树的每层都记录一个值,表示从根dfs到现在为止这层的总值,然后考虑dfs的过程,发现刚刚遍历到这个点的时候之前的点已经被记录到这个数组里了,然后显然这个点能拥有的城池可以通过先加上当前这个点能到达的最大层数的总值,也就是之前遍历到的这一层的值,然后等遍历完当前点的子树之后再减去那层的值,可以发现现在如果加上当前点的子树大小就是符合要求的城池的人数。 -
逃跑

思路
发现L相等,又注意到求最多,想到可以记录每个点到根节点的距离,然后在这个链上面直接二分找到第一个不大于L的值,然后这一段就可能多一个羊,所以再树上差分做一下就行了。 -
树上最多不相交路径

思路
考虑贪心,先对询问的点对进行lca的排序,然后按照层数从大到小进行排序,然后选,发现这样是优的,对于一个点对,如果被选了,那就把这个点对的lca的子树都标记为不能选,因为是按lca排序的,所以后面的lca肯定在它上面,所以如果后面的点对有在这个lca的子树里的话就肯定会经过这个lca,就不行了。 -
树上三角形

思路
不会,看的题解。发现三个数不是三角形就是两个边之和小于等于第三条边,发现从1到\(2^31\)之间最多有47个数使得它们在一起都组不成三角形,是由前两个数加起来得到的第三个数和它自己加起来得到的,一共最多47个,所以如果这条路径上的点大于47的话,那就必然是有解的,小于的话那复杂度也很小,直接暴力检查就行
动态规划
-
录制唱片

思路
多组背包 -
路短最

思路
最长路和暴力都能过 -
POI2012 Cloakroom

思路
先考虑\(a_i,b_i\)的限制,发现直接排序就行,然后考虑\(c_i\)的限制,发现就是背包 -
奶牛看电影
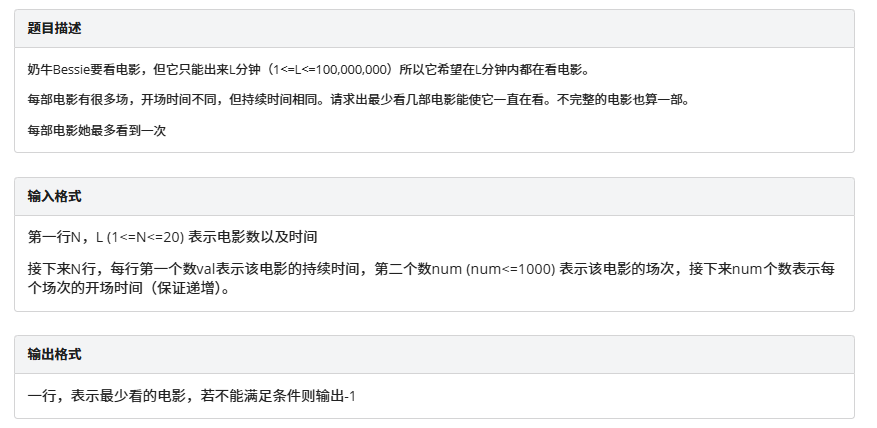
注意到数据范围很小,直接状压直接二分就行 -
[BZOJ1399]Win

思路
考虑状压+递归,对于每棵子树考虑方案,然后乘起来 -
Coci2009 podjela

树形dp,\(f_{i,k}\)表示以i为根的子树内操作k次后满足所需能剩下的最多金币,那么显然如果一个点的某个子节点的值大于0,那就是可选可不选,如果小于零,就必须选,最后判断一下就行了。
字符串
-
POI2010 Antisymmetry
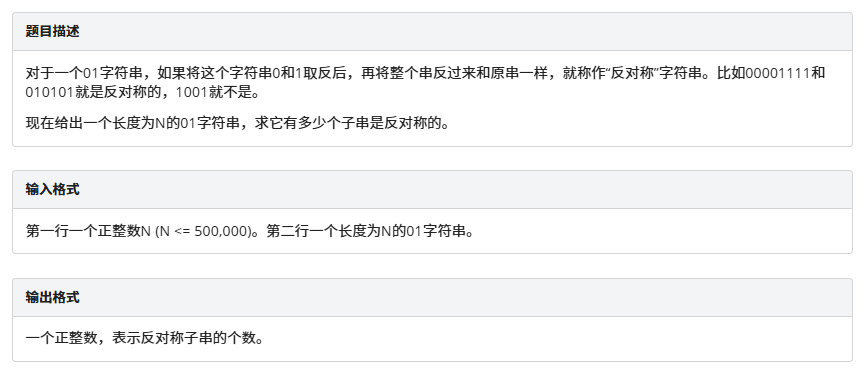
思路
不难想到可以先把原串的先后的0/1反过来,然后把它和原串的hush处理出来,这样就可以做到\(O(1)\)查询,然后现在考虑怎么做,发现如果某个串符合条件,那么和它的中心相同的且长度比它小的串也肯定是符合条件的,同时发现,一个符合条件的串肯定是长度为偶数的,所以就自然想到了枚举中点进行二分。 -
Bovine Genomics
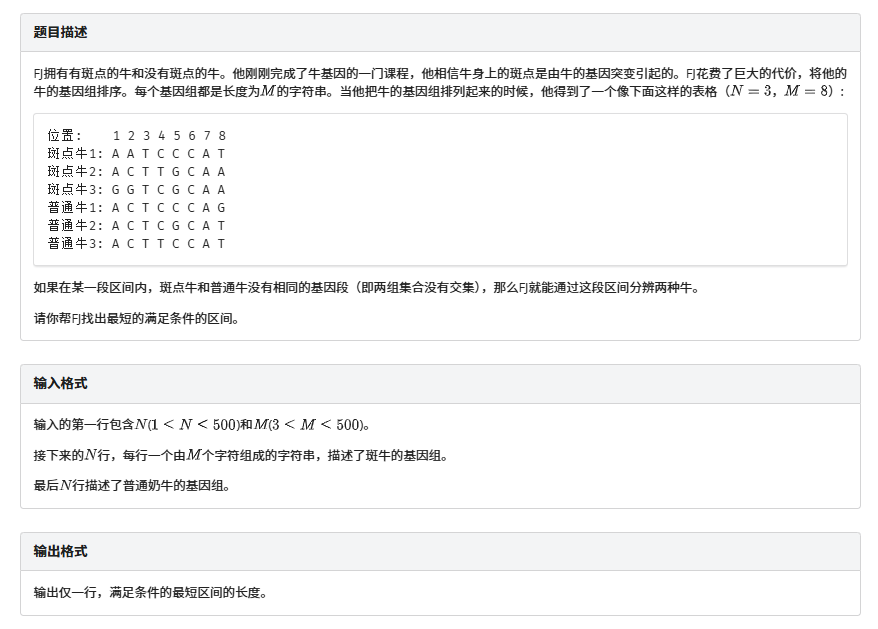
思路
\(O(n^2)\)找区间,然后对于每个区间对于普通和斑点的都跑一遍hush,排序,双指针找就行了。 -
friends
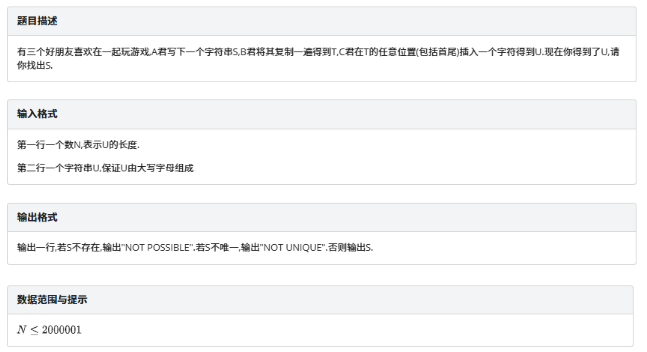
思路
枚举插入节点,然后hush判断左右两边


 浙公网安备 33010602011771号
浙公网安备 33010602011771号