20241021

今天的模拟赛打的比较舒服。
但是还要早起跑操+早读+升旗就不太好。
去升旗之前做了第一题，简单的模拟，感觉这很符合cspsT1的难度啊，之前的感觉都有点难了。

• 【贪吃蛇】
  题意：
  思路：直接用桶记录蛇的位置，考虑怎么记录加和减操作，可以考虑用STL，但是直接维护两个指针也可以。
  代码：

#include <iostream>
#include <cstdio>

using namespace std;
const int N = 110;

int n, m, t, q, x, y, op;
int head, tail = 1, ans;
int a[N][N];
bool b[N][N];
bool flag = 0;
char c;
struct Snake { int x, y; } s[N * N];

void work () {
	if(c == 'U') --x;
	if(c == 'D') ++x;
	if(c == 'L') --y;
	if(c == 'R') ++y;
} 

int main () {
	freopen("snake.in", "r", stdin);
	freopen("snake.out", "w", stdout);
	scanf("%d%d%d%d", &n, &m, &t, &q);
	while(t--) {
		scanf("%d%d", &x, &y);
		b[x][y] = 1;
	}
	scanf("%d%d", &x, &y);
	b[x][y] = 1, s[++head] = {x, y};
	while(q--) {
		++ans;
		scanf("%d", &op);
		if(op == 1) {
			scanf("%s", &c);
			x = s[head].x, y = s[head].y;
			work();
			if(b[x][y] || x < 1 || x > n || y < 1 || y > m) {
				flag = 1; break;
			}
			s[++head] = {x, y}, b[x][y] = 1;
		} else {
			x = s[tail].x, y = s[tail].y;
			b[x][y] = 0;
			++tail;
		}
	}
	if(flag) printf("%d\n", ans);
	else puts("-1");
	return 0;
}

• 【分糖果】
  题意：参考 皇后游戏
  思路：考场上没推出来具有传递性的，只推出来 $\min(a_i, b_j) \leq \min(a_j, b_i) $，然后就打上去交了，没想到过了，应该是数据比较水吧。具体思路可以直接看题解，因为markdown太长了我不想打就不写了。
  代码：

#include <iostream>
#include <algorithm>

using namespace std;
typedef long long ll;
const int N = 2e4 + 10;

int T, n;
ll c[N];
struct zx {
	int x, y, d;
	bool operator < (zx a) const {
		if(a.d != d) return d < a.d;
		if(d <= 0) return x < a.x;
		else return y > a.y;
	}
} a[N];

int main() {
	cin >> T;
	while(T--) {
		cin >> n;
		for(int i = 1; i <= n; ++i) {
			cin >> a[i].x >> a[i].y;
			if(a[i].x == a[i].y) a[i].d = 0;
			if(a[i].x < a[i].y) a[i].d = -1;
			else a[i].d = 1;
		}
		sort(a + 1, a + n + 1);
		ll s = 0;
		for(int i = 1; i <= n; ++i) {
			s += a[i].x;
			c[i] = max(s, c[i - 1]) + a[i].y;
		}
		cout << c[n] << endl;
	}
	return 0;
}

• 【排序】
  题意：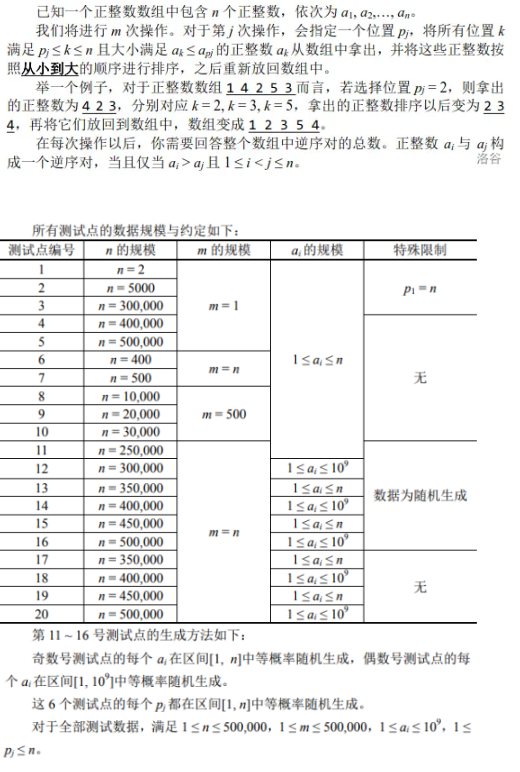
  思路：考场上没时间想这道题了，所以就直接写了个归并拿了点分，本来预计有50的，结果没开long long挂了15。正解应该是线段树。考虑每次操作完之后以被排序过的数为一个数的话它的后面就没有比他小的了，很显然，因为排完序了小的都在它前面了。所以每次的排序操作其实就是在原数列上把\(p_j\)之后的大于等于它的数的逆序对值改成零就行了。那就可以考虑维护一下他有没有被排过序，再维护一个区间最小值来判断更新是否需要进入这个区间更改是否排序状态，再维护一个区间逆序对和就行了。
  代码：

#include <cstdio>
#include <iostream>
#include <algorithm>
#define ls (x << 1)
#define rs (x << 1 | 1)

using namespace std;
typedef long long ll;
const int N = 5e5 + 10;
const ll inf = 1e9 + 7;

int n, m, x;
ll a[N], b[N], c[N], ans[N], vis[N];
struct S { ll l, r, s, mn; } t[N << 2];

int lowbit (int x) {
    return x & -x;
}

void update (int k) {
    for(int i = k ;i <= n ;i += lowbit(i))
        c[i] += 1;
}

ll sum (int k) {
    ll res = 0;
    for (int i = k; i >= 1 ;i -= lowbit(i))
        res += c[i];
    return res;
}

void pushup (int x) {
	t[x].s = t[ls].s + t[rs].s;
	t[x].mn = min(t[ls].mn, t[rs].mn);
}

void build (int x, int l, int r) {
	t[x].l = l, t[x].r = r;
	if(l == r) {
		t[x].s = ans[l], t[x].mn = a[l];
		return;
	}
	int mid = (l + r) >> 1;
	build(ls, l, mid), build(rs, mid + 1, r);
	pushup(x);
}

ll modify (int x, int k) {
	if(!t[x].l) return 0;
	int l = t[x].l, r = t[x].r, mid = (l + r) >> 1;
	if(l == r) 
		return t[x].mn;
	if(k <= mid) return modify(ls, k);
	else return modify(rs, k);
}

void change (int x, int L, int R, int k) {
	if(!t[x].l||t[x].mn>k) return;
	int l = t[x].l, r = t[x].r, mid = (l + r) >> 1;
	if(l >= L && r <= R) {
		if(t[x].mn <= k) {
			if(l == r) {
				t[x].mn = inf, t[x].s = 0;
			} else {
				change(ls, L, R, k), change(rs, L, R, k);
				pushup(x);
			}
			
		} else return;
	} else {
		if(L <= mid) change(ls, L, R, k);
		if(R > mid) change(rs, L, R, k);
		pushup(x);
	}
}

int main () {
	freopen("sort.in", "r", stdin);
	freopen("sort.out", "w", stdout);
    scanf("%d%d", &n, &m);
    for(int i = 1; i <= n; ++i)
        scanf("%d", &a[i]), b[i] = a[i];
    sort(b + 1, b + n + 1);
    int cnt = unique(b + 1, b + 1 + n) - b - 1;
    for (int i = 1; i <= n; ++i)
        a[i] = lower_bound(b + 1, b + 1 + cnt, a[i]) - b;
    for(int i = n; i >= 1; --i) {
        update(a[i]);
		ans[i] = sum(a[i]) - 1;
    	ans[i] -= vis[a[i]], vis[a[i]]++;
    }
    build(1, 1, n);
    while(m--) {
    	cin >> x;
    	ll sum = modify(1, x);
    	if(sum != inf) 
    		change(1, x, n, sum);
    	printf("%lld\n", t[1].s);
	}
	return 0;
}