matlab矩阵基础

矩阵的建立

（1）一般矩阵

>> [1,2,3;4,5,6;7,8,9]

ans =

     1     2     3
     4     5     6
     7     8     9

（2）分块矩阵

>> A = [1,2,3;4,5,6;7,8,9];
>> B = [-1,-2,-3;-4,-5,-6;-7,-8,-9];
>> C=[A,B;B,A];

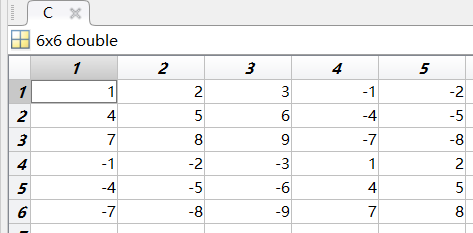
（3）复数矩阵

>> C=[A,B;B,A];
>> B = [1,2,3;4,5,6];
>> C = [6,7,8;9,10,11];
>> A = B + i*C;

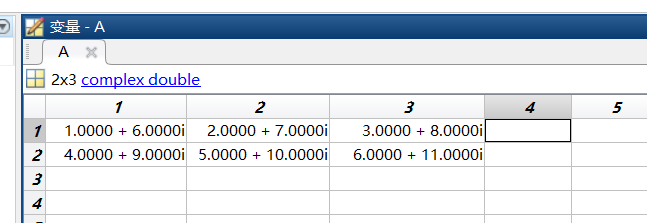
结构矩阵和单元矩阵

（1）结构矩阵

格式为：结构矩阵元素.成员名 = 表达式;

原理同C语言还是一样的！

>> a(1).x1 = 10;a(1).x2 = 'liu';a(1).x3 = [11,21;34,78];
>> a(2).x1 = 12;a(2).x2 = 'wang';a(2).x3 = [34,191;27,578];
>> a(3).x1 = 14;a(3).x2 = 'cai';a(3).x3 = [13,890;67,231];

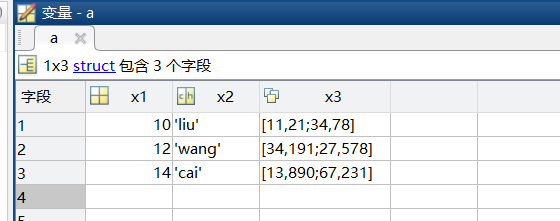
（2）单元矩阵

和一般矩阵相似，直接输入就行，然后用大括号括起来；

>> b = {10,'liu',[11,21;34,78];12,'wang',[34,191;27,578];14,'cai',[13,890;67,231]}

b =

  3×3 cell 数组

    {[10]}    {'liu' }    {2×2 double}
    {[12]}    {'wang'}    {2×2 double}
    {[14]}    {'cai' }    {2×2 double}

冒号表达式

e1 : e2 : e3

e1为初始值，e2为等差，e3为终止值；

>> t = 0:1:5
t =
     0     1     2     3     4     5
>> t = 0:5
t =
     0     1     2     3     4     5

linspace(a,b,n)函数

a为初始值，b为终止值，n为数组总长度；

>> t = linspace(0,pi,6)
t =
         0    0.6283    1.2566    1.8850    2.5133    3.1416

　　

　　

矩阵元素的引用

（1）直接通过下标来引用矩阵的元素

>> A = [1,2,3;4,5,6];
>> A(4,5) = 10;//这里4，5明显超出了原数组大小，自动把A矩阵定义成4行5列；

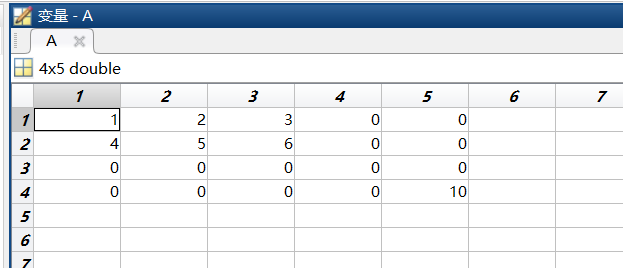
（2）通过序号引用

>> A = [1,2,3;4,5,6];
>> A(3)
ans =
     2

其中A(1) = 1,A(2) = 4, A(3) = 2；//不是平常的先从左往右而是从上往下；

sub2ind()函数：

>> A = [1:3;4:6];
>> D = sub2ind(size(A),[1,2;2,2],[1,1;3,2])//后面两个矩阵分布代表了矩阵 D 的行，列；

D =

     1     2  //A(1,1) = 1;A(2,1) = 2;
     6     4  //A(2,3) = 6;A(2,2) = 4;

 

ind2sub函数：

>> [I,J] = ind2sub([3,3],[1,3,5])

I =
     1     3     2
J =
     1     1     2

I，J  就是在一个 [ 3, 3] 矩阵中序列号分别为1，3，5下标的 行和列；

利用冒号表达式获得子矩阵：

>> A=[1,2,3,4,5;6,7,8,9,10;11,12,13,14,15];
>> A(1 : 2,:)//获得第1至2行的所有元素
ans =
     1     2     3     4     5
     6     7     8     9    10
>> A(2:3,1:2:5)//获得第2至3行的，1到5之间等差为2的元素
ans =
     6     8    10
    11    13    15

end运算符：

>> A=[1,2,3,4,5;6,7,8,9,10;11,12,13,14,15;16,17,18,19,20];
>> A(end,:)
ans =
    16    17    18    19    20
>> A([1,4],3:end)//引用第一行和第三行
ans =
     3     4     5
    18    19    20

删除矩阵中元素的值：

>> A=[1,2,3,0,0;7,0,9,2,6;1,4,-1,1,8]
A =
     1     2     3     0     0
     7     0     9     2     6
     1     4    -1     1     8
>> A(:,[2,4]) = []//让他等于空矩阵，必然删除的是某一行某一列
A =
     1     3     0
     7     9     6
     1    -1     8

矩阵转置：

>>  x = 1:12
x =
     1     2     3     4     5     6     7     8     9    10    11    12
>> y = reshape(x,4,3)
y =
     1     5     9
     2     6    10
     3     7    11
     4     8    12
>> x = reshape(y,3,4)
x =
     1     4     7    10
     2     5     8    11
     3     6     9    12
>> y = x(:)//x(:) == reshape(x,12,1);
y =
     1
     2
     3
     4
     5
     6
     7
     8
     9
    10
    11
    12