Lua练习题 第三章

2021-07-05

本文部分内容来自  https://blog.csdn.net/qq_44800780/article/details/101060427
实践与网上学习结合

3.1

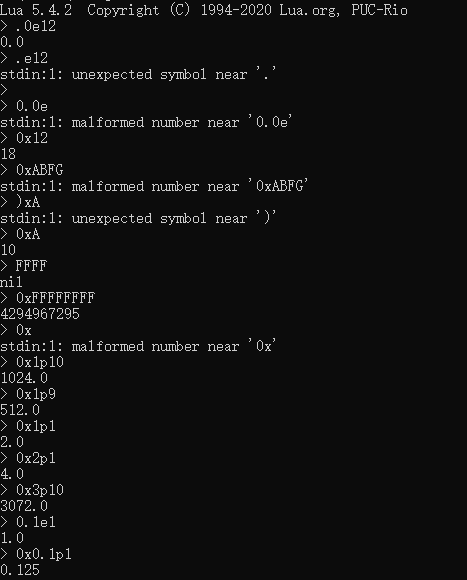
3.2

练习3.2
math.maxinterger *2 左移一位 0x1111…变成1111…10 对应的值就是-2
math.mininteger * 2 左移 10000…00 左移 000000 对应的值为0
math.maxinteger * math.maxinteger 0x1111 * 0x1111 进位后变成0x0000001结果为1
math.mininteger * math.mininteger 0x100000… * 0x10000… 最高位进位 最后变成0x000… 结果位0

3.3

• a % b == a - ((a // b) * b)
• a // b得到的商向负无穷取整

　　

> for i =-10,10 do
>> print(i,i%3);end
-10     2
-9      0
-8      1
-7      2
-6      0
-5      1
-4      2
-3      0
-2      1
-1      2
0       0
1       1
2       2
3       0
4       1
5       2
6       0
7       1
8       2
9       0
10      1

3.4

> 2^3^4
2.4178516392293e+024
> 26-3……4
stdin:1: unexpected symbol near '26'
> 2^-3^4
4.1359030627651e-025
> 2^81
2.4178516392293e+024
>

练习3.5

12.7可以表示为以10为底的幂作为分母的分数，是否可以找到一个整数除以2的n次方得到结果为12.7即 x / 2^n = 12.7 以及 x / 2 ^ n = 5.5 x要求为整数
解决思路 从2的一次方开始 找到整数就返回

function find(num)
    local i = 0
    for j = 1,63 do
        if(math.tointeger(num * 2^j) ~= nil) then
            print(num * 2^j,"/",2^j,"==",num)
        end
    end
end
find(12.7)
find(5.5)

 

练习3.6

v = s* h/ 3
其中S是圆柱的底面积，h是圆柱的高，r是圆柱的底面半径。

function CalConevolume(h,angle)
    return ((math.tan(math.rad(angle)*h)^2.0*math.pi))*h / 3
end

 

练习3.7The Box–Muller transform 把一对均匀分布随机数映射到一对标准正态分布随机数。它有两种形式：
基本形式：用(0,1) (0,1)(0,1)均匀分布随机数，需要计算三角函数sin \sinsin和cos \coscos；
极坐标形式：用(−1,1) (-1,1)(−1,1)均匀分布随机数，且不需要计算三角函数。

function BoxMuller()
    local x = math.random()
    local y = math.random()
    x = (x==0) and 1 or x
    y = (y==0) and 1 or y
    return math.sqrt(-2*(math.log(x))) * math.sin(2*math.pi*y)
end

print(BoxMuller())