查找——数据结构与算法学习

查找算法

二分查找（初始二分查找）

算法原理：就是一个分治的思想：分而治之，不断划分数据的查找范围，就可以提高查找效率，效率达到了O(logn)

前提：必须对应的是有序列表

//手写二分法，需求是返回索引
    public static int binarySearch3(int[] arr,int left,int right,int findVal){
        if(left > right){
            return -1;//这是退出索引的条件，说明没有返回数据
        }
        int mid = (left + right)/2;//中间的索引
        int midVal = arr[mid];
        if(findVal > midVal){
            return  binarySearch3(arr,mid + 1,right,findVal);//向右递归
        }else if(findVal < midVal){
            return binarySearch3(arr,left,mid - 1,findVal);//向左递归
        }else{
            return mid;//相当于此时midVal = arr[mid],现在只是找回索引而已。
        }
    }

——二分查找法（非递归）

---

 public static int binarySearch(int arr[],int target){
        int left = 0;
        int right = arr.length - 1;
        while(left <= right){
            int mid = (left + right)/2;
            if(arr[mid] == target){
                return mid;
            }else if(arr[mid] < target){
                left = mid + 1;//注意这里是mid，而不是left
            }else{
                right = mid - 1;
            }
        }
        return -1;
    }

——但是遇到如果查询的数字有多个的怎么办呢？这时就要引入数组的思想来进行优化。

//优化版的查找算法，能够完全查找出全部的数据
    public static List<Integer> binarySearch2(int arr[],int left,int right,int findVal){
        if(left > right){
            return new ArrayList<Integer>();
        }
        int mid = (left + right)/2;
        int midVal = arr[mid];

        if(findVal > midVal){
            return binarySearch2(arr,mid + 1,right,findVal);
        }else if(findVal < midVal){
            return binarySearch2(arr,left,mid - 1,findVal);
        }else{
            ArrayList<Integer> integers = new ArrayList<>();
            //向左扫描，满足1000的元素加入集合ArrayList
            int temp = mid - 1;
            while(true){
                if(temp < 0 || arr[temp] != findVal){
                    break;
                }
                integers.add(temp);
                temp --;
            }
            integers.add(temp);
            //向右扫描，满足1000的元素加入集合ArrayList
            temp = mid + 1;
            while(true){
                if(temp > arr.length - 1 || arr[temp] != findVal){
                    break;
                }
                integers.add(temp);
                temp ++;
            }
            return integers;
        }
    }

思考：加入了使用while(true)结构进行扫描，真的很有才。

插值查找（插值二分查找）

算法原理：就是在二分查找的基础上补充了一个自适应索引

对应的代码公式：

int mid = left + (right – left) * (findVal – arr[left]) / (arr[right] – arr[left])

适用于数据量较大，关键字分布比较均匀的查找表中。

斐波那契查找（黄金分割法二分查找）

算法原理：就是在二分查找的基础上引入黄金分割的思想

关键：为什么 mid=low+F(k-1)-1，F(k-1)-1区间是为什么？

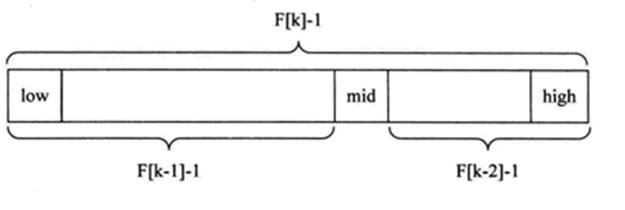
通过设计该算法：使正好该数列中空出一个mid位置

public static int[] fib(){
        int[] f = new int[maxSize];
        f[0] = 1;
        f[1] = 1;
        for (int i = 2; i < maxSize ; i++) {
            f[i] = f[i - 1] + f[i - 2];
        }
        return f;
    }

    public static int fibSearch(int a[],int key){
        int low = 0;
        int high = a.length - 1;
        int k = 0;
        int mid = 0;
        int f[] = fib();
        while(high > f[k] - 1){
            k++;
        }
        int[] temp = Arrays.copyOf(a, f[k]);
        for(int i = high + 1; i < temp.length; i++) {
            temp[i] = a[high];
        }
        while(low <= high){
            mid = low + f[k - 1] - 1;
            if(key < temp[mid]){
                high = mid - 1;
                k--;//这个是由斐波那契数列所拆开来的
            }else if(key > temp[mid]){
                low = mid + 1;
                k -= 2;//这个是由斐波那契数列所拆开来的
            }else{
                if(mid <= high){
                    return mid;
                }else{
                    return high;
                }
            }
        }
        return -1;
    }