CF 2138F Ode to the Bridge Builder

非常好几何题。
最后一部分参考了 Milmon 大神的代码，非常感谢！

首先能够发现 \(m = \left\lceil2|AC|\right\rceil\)。
又因为题目要求了 \(0.5\le l\le 1\)，这说明即使每条边都贴在 \(AC\) 上至少也需要 \(\lceil|AC|\rceil\) 个三角形。
并且每一步都能加一个贴着 \(AC\) 三角形是不太现实的，于是我们尝试构造使得每 \(2\) 个三角形能够让与 \(C\) 的距离减掉 \(1\)。

那么尝试让第一个三角形就贴着 \(AC\)，能够构造出如下的平行四边形式的构造（按字典序为构造顺序）：

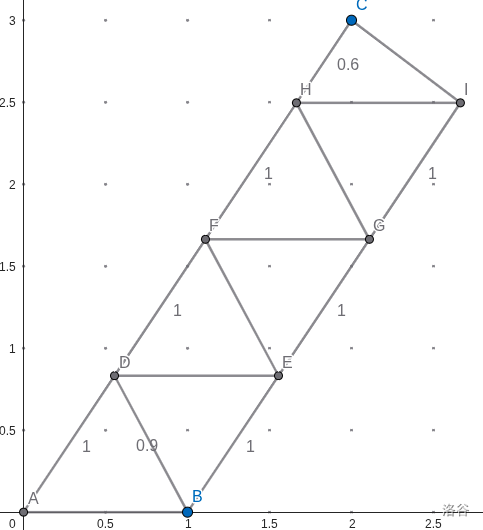
不过这样有个问题就是当 \(|CF| < 1.5\) 时，分割出来的 \(|CH| < 0.5\) 不合法。

对此，因为 \(1 < |CF|\le 2\)，可以考虑把最后一步的点改为 \(CF\) 中点，即：

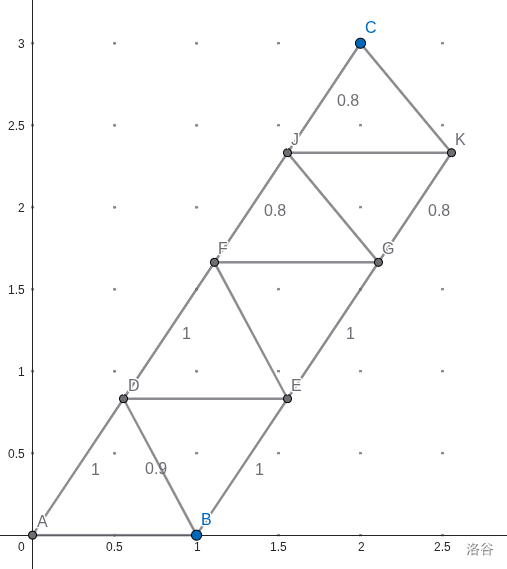
分析对应的步数，能够发现只需要 \(2\lceil|AC|\rceil - 1\) 步，当 \(0 < \{|AC|\} < 0.5(\{x\} = x - \lfloor x\rfloor)\) 时会恰好等于 \(\lceil 2|AC|\rceil\)，否则能够多出来一步。

不过这个构造方法肯定不是通用的，现在只保证了 \(AC, BK\) 上的线段和 \(AB\) 的平行线段的长度，还有 \(BD, CK\) 没有考虑。

记 \(\theta = \angle CAB\)。

首先来考虑 \(BD\)：
使用余弦定理：\(|BD|^2 = |AB|^2 + |AD|^2 - 2|AB||AD|\cos \theta = 2(1 - \cos \theta)\)。
结合 \(0.5\le |BD|\le 1\)，可以得到 \(\frac{1}{2}\le \cos\theta \le \frac{7}{8}\)。

尝试代入常用角，会发现 \(30\degree, 60 \degree\) 都合法，于是至少 \([30\degree, 60\degree]\) 内的角都合法。
于是应当要有 \(30\degree\le \theta\le 60\degree\)。

接下来考虑 \(CK\)：
依然是余弦定理：\(|CK|^2 = |CJ|^2 + |JK|^2 - 2|CJ||JK|\cos \theta = 1 + |JK|^2 - 2|JK|\cos \theta\)。

首先因为 \(1 + |JK|^2 - 2|JK|\cos \theta = 1 + |JK|(|JK| - 2\cos \theta) \le 1 + |JK|\times 0 = 1\)，所以 \(|JK|\not > 1\)。
接下来把 \(|JK|\) 视作自变量，该二次函数最小值在 \(|JK| = \cos \theta\) 取到，又因为 \(\frac{1}{2}\le \cos \theta \le \frac{7}{8}\) 所以可以取到，此时最小值为 \(1 - \cos^2 \theta\ge \frac{1}{4}\)（注意此处代入的就是 \(\theta = 60\degree\) 了），于是 \(|CK|^2\ge \frac{1}{4}\) 合法。

于是只要 \(30\degree\le \theta \le 60\degree\)，这个构造就是合法的。

那么如果 \(\theta < 30\degree \lor \theta > 60\degree\) 怎么办呢？
刚刚的构造其实已经非常好了，我们尝试继续复用这个结构。

因为这个结构只需要满足 \(30\degree \le \theta\le 60\degree\)，于是我们考虑构造一个合法的 \(\theta'\) 出来。
具体来说，发现当 \(\theta < 30\degree\) 时，可以考虑构造 \(\theta = \alpha - \theta'(30\degree \le \alpha, \theta' \le 60\degree)\)；当 \(\theta > 60\degree\) 时，可以考虑构造 \(\theta = \beta + \theta'(30\degree\le \beta, \theta'\le 60\degree)\)。

如图：

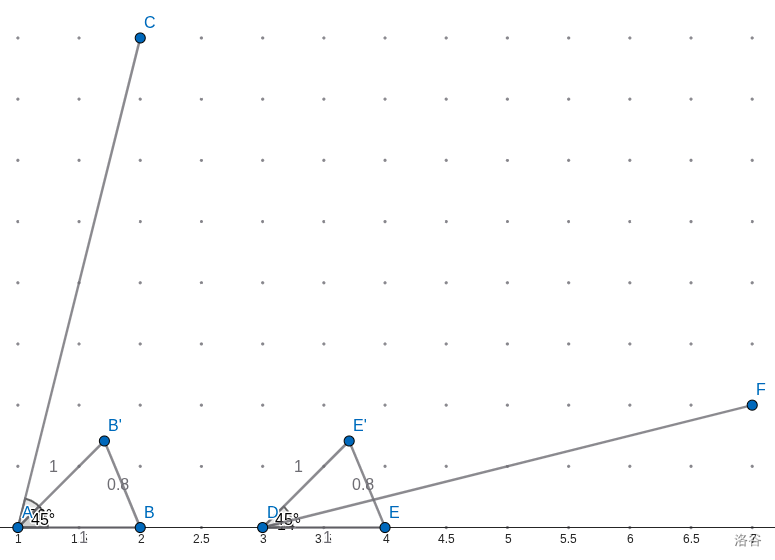
对于 \(\angle CAB\)，接下来就可以考虑把 \(x\) 轴变为 \(AB'\) 直线；对于 \(\angle EDF\)。接下来就可以考虑把 \(x\) 轴变为 \(DE'\) 直线。
在变化之后，\(AC, DF\) 于其对应的 \(x\) 轴的夹角就满足了限制。

不过此时有一个问题是，我们多引入了一个三角形。
当 \(\{|CA|\} = 0\lor \{|CA|\} > 0.5\) 时，刚好前面的构造还剩了一个可以用上。
不过当 \(0 < \{|CA|\} \le 0.5\) 时，就会多出一次步数。

第一次显然是省不了的，那就只能省掉后面平行四边形的步数了。
不过在叠加的过程，平行四边形的 \(2\) 个三角形看起来是必须的。
那么最后也只能尝试在最后 \(3\) 个三角形进行一些优化了。

也就是说，当剩下的 \(|AC|\) 在 \(1\) 到 \(1.5\) 之间时，我们需要尝试使用 \(2\) 个三角形进行构造。
首先因为长度 \(> 1\)，所以两个三角形肯定都需要有一条边贴着 \(|AC|\)。

但是这个时候若 \(\theta'\) 近似于 \(60 \degree\)，似乎不管怎么都构造不出来，好像倒闭了？（我就在这里倒闭了。）
此时回归 \(\theta'\) 的定义，会发现 \(\theta'\) 并不会是个定值，而是会根据 \(\theta\) 有着不同的取值区间，于是直接认为 \(\theta'\) 是个定值是不正确的。

那还是继续考虑什么情况 \(\theta'\) 会合法吧。

确定的是，最后一定会有 \(|BC|\) 这条边，并且对于 \(AC\) 上选出的第一个三角形的端点 \(D\)，一定有 \(|BD|\le \max\{|BA|, |BC|\} = \max\{1, |BC|\}\)。
于是对于上界，我们只需要考虑 \(|BC|\le 1\)。

还是余弦定理：\(|BC|^2 = |AB|^2 + |AC|^2 - 2|AB||AC|\cos \theta' = 1 + |AC|^2 - 2|AC|\cos \theta'\le 1\)。
所以这说明 \(|AC|\le 2\cos \theta'\)，推出 \(\cos\theta'\ge \frac{3}{4}\)。

那么会发现取 \(\theta'\) 一定满足条件，并且很惊喜的一点是，能够发现 \(\theta' = 30\degree\) 一定时能被构造出的。
当 \(\theta < 30\degree\) 时，可以取 \(\alpha = \theta + 30\degree\)；当 \(\theta > 60\degree\) 时，可以取 \(\beta = \theta - 30\degree\)。

接下来就需要考虑一下 \(D\) 的问题了，因为 \(|AD|,|CD|\) 的长度都需要合法，所以考虑 \(|AC|\) 长度趋近于 \(1\) 的情况，此时只能选择 \(D\) 为 \(AC\) 的中点。

接下来只需要考虑下界的问题了。

• 对于 \(BC\)：\(|BC|^2 = 1 + |AC|^2 - \sqrt{3}|AC|\)，对称轴为 \(\frac{\sqrt{3}}{2}\)，结合定义域，当 \(|AC| = 1\) 时取到最小值 \(2 - \sqrt{3} \approx 0.26 \ge \frac{1}{4}\)。
• 对于 \(BD\)：\(|BD|^2 = 1 + \frac{1}{4}|AC|^2 - \frac{\sqrt{3}}{2}|AC|\)，对称轴为 \(\sqrt{3}\)，结合定义域，当 \(|AC| = \sqrt{3}\) 时取到最小值 \(1 + \frac{3}{4} - \frac{3}{2} = \frac{1}{4}\)，甚至刚刚好。

于是对于上述的情况，只需要取 \(AC\) 中点，第一步扩展 \(\triangle ABD\)，第二步扩展 \(\triangle BCD\)，就解决了这个情况。

时间复杂度为 \(\mathcal{O}(m)\)，代码非常好写。

#include <bits/stdc++.h>

const double pi = acos(-1);
constexpr int N = 3e5 + 10;

int u[N], v[N];
double sx[N], sy[N];

inline void solve() {
    int x, y;
    scanf("%d%d%*d", &x, &y);
    double d = hypot(x, y);
    double th = atan2(y, x);
    double sint = 1.0 * y / d;
    double cost = 1.0 * x / d;

    int a = 1, b = 2, m = 2;
    sx[1] = 0.0, sy[1] = 0.0;
    sx[2] = 1.0, sy[2] = 0.0;
    auto add = [&](double x_, double y_) {
        m++;
        u[m] = a, v[m] = b;
        sx[m] = x_, sy[m] = y_;
        return m;
    };

    if (th > pi / 3) {
        b = add(cos(th - pi / 6), sin(th - pi / 6));
    }
    if (th < pi / 6) {
        b = add(cos(th + pi / 6), sin(th + pi / 6));
    }

    while (d > 2) {
        a = add(sx[a] + cost, sy[a] + sint);
        b = add(sx[b] + cost, sy[b] + sint);
        d -= 1;
    }

    a = add(sx[a] + d / 2.0 * cost, sy[a] + d / 2.0 * sint);
    if ((pi / 6 <= th && th <= pi / 3) || d > 1.5) {
        b = add(sx[b] + d / 2.0 * cost, sy[b] + d / 2.0 * sint);
    }
    a = add(x, y);

    printf("%d\n", m - 2);
    for (int i = 3; i <= m; i++) {
        printf("%d %d %.10lf %.10lf\n", u[i], v[i], sx[i], sy[i]);
    }
}

int main() {
    int t;
    scanf("%d", &t);
    while (t--) {
        solve();
    }
    return 0;
}