剑指offer11_二进制中1的个数_题解

二进制中1的个数

题目描述

输入一个整数，输出该数32位二进制表示中1的个数。其中负数用补码表示。

示例1

输入

10

返回值

2

分析

方案一：二进制移位法

将整数看成二进制，让掩码mask从右往左与n的每一位进行&操作，若与操作结果为1，则n的当前位为1，bits加1，否则当前位为0，继续左移mask。

/**
时间复杂度:O(32)
空间复杂度:O(1)
**/
class Solution
{
public:
    int NumberOf1(int n){
        int bits = 0;
        int mask = 1;
        for(int i = 0; i < 32; i++){
            if((n & mask) != 0){
                bits++;
            }
            mask <<= 1;
        }
        return bits;
    }
};

思考

• 为什么不采用从左往右移位？
  • 如果n本身为负数（负数在计算机中用补码表示）向右移位最高位补1。程序会产生死循环

class Solution
{
    int NumberOf1(int n)
    {
        int bits = 0;
        while (n != 0)
        {
            if ((n & 1) != 0)
            {
                bits++;
            }
            n >>= 1;
            cout << n << endl;
        }
        return bits;
    }
};

栗子：假设 \(n=-1\) ，则\(n\) 的原码和补码表示分别为

\[1000,0001\tag{原码} \]

\[1111,1111\tag{补码} \]

-1的补码右移结果还是\(1111,1111\)，也就是说-1右移的结果还是-1

故n无法减为0，产生死循环

方案二：巧用 \(n\&(n-1)\)

\(n\&(n-1)\) 解析： 二进制数字 \(n\) 最右边的 \(1\) 变成 \(0\) ，其余不变。

/**
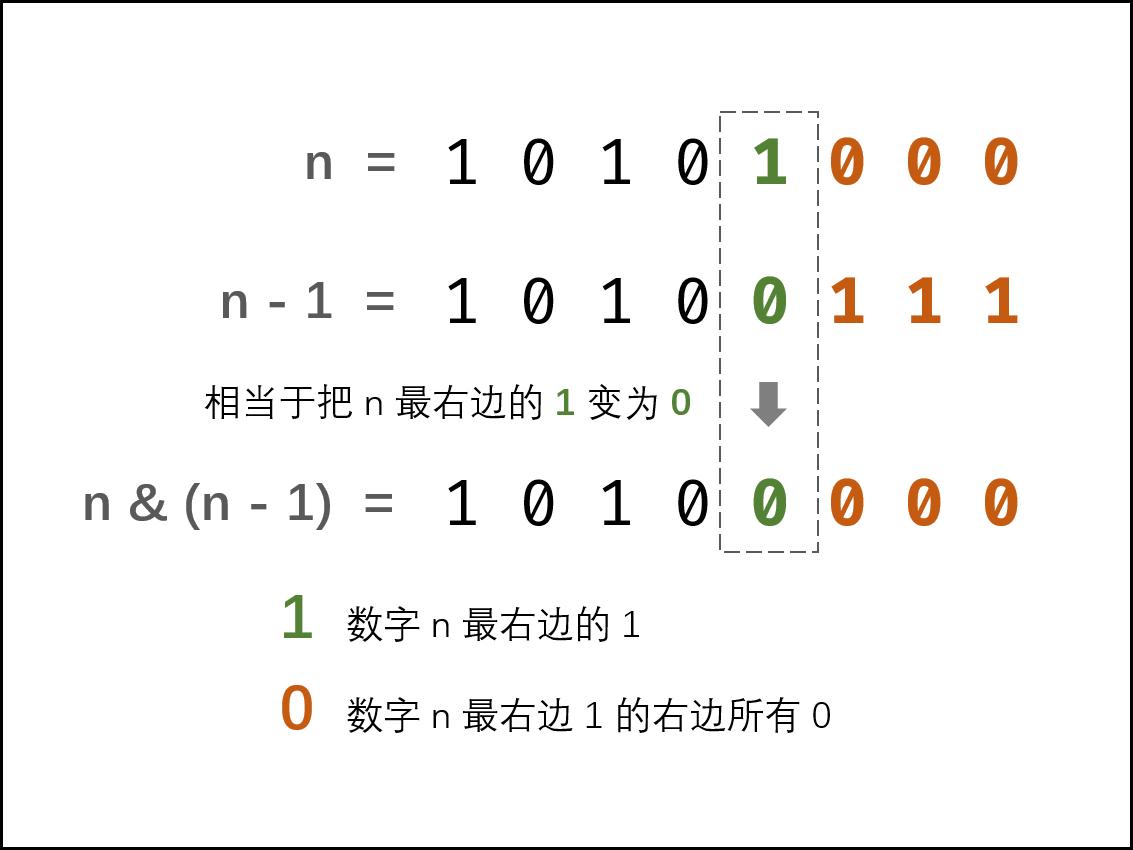
时间复杂度:O(n)
设 M 为二进制数字 n 中 1 的个数，则需循环 M 次（每轮消去一个 1 ），占用 O(M)。
空间复杂度:O(1)
**/
class Solution
{
public:
    int NumberOf1(int n){
        int sum = 0;
        while (n != 0){
            sum++;
            n &= (n - 1);
        }
        return sum;
    }
};

方案三：bitset

C++的 bitset 在 STL 的 bitset 头文件中，它是一种类似数组的结构，它的每一个元素只能是０或１，每个元素仅占用１bit 空间。

class Solution
{
public:
    int NumberOf1(int n){
        bitset<32> bs(n);
        return bs.count();// 返回1的个数
    }
};