AtCoder Beginner Contest 229(F,G)

AtCoder Beginner Contest 229(F,G)

F(二部图,dp)

F

这个题大致是给你\(n+1\)个点，为\(0\)到\(n\),然后\(n\)条边是点\(0\)到\(1...n\)这些点的\(n\)条边，后面还有\(n\)条边，连接点\(i\)和\(i+1\)(其中\(i\)为\(1\)到\(n\),其中\(n\)是和\(1\)连接的)

前\(n\)条边的价值是\(a_i\),后面\(n\)条边的价值是\(b_i\),我们需要删除一些边，使得这个图变成一个二部图，其中删除每一条边的价值如上，问得到一个二部图的最小价值为多少

对于二部图，我的理解就是可以把一个图的点分成两个集合，两个集合的不同点可以互相相连，但是同一集合里面的点一定是不连通的

那么，对于这些点，我们也可以分成两个集合

设两个集合，编号为\(0\)和\(1\),我们先让点\(0\)在集合\(0\)，然后对于其他的点，我们需要判断是否在一个集合，如果在同一个集合，那么需要删除相连的边，取较小的

我们可以从\(1\)到\(n\)一个一个的选择，但是，假如此时选择的是\(i\)的分配，我们只需要按照上一个进行判断即可了，但是还有一个边，就是点\(n\)和\(1\),那么第\(n\)的点的选择要删除的边不仅仅和\(n-1\)个点的关系，还需要和\(1\)的点的关系，所以，我们不仅需要知道最新点的选择，还需要知道第一个点的选择

\(dp[i] [x] [y]\)其中\(i\)是我们1到\(i\)的点都已经分配好了，其中点\(i\)在集合\(x\),而点\(1\)在集合\(y\)

#include <iostream>
#include <algorithm>
#include <vector>
#include <string>
#include <map>
#include <set>
#include <queue>
#include <stack>
#include<cmath>
#include <unordered_map>
#include <array>
#include <cstring>
#include <bitset>
#include <numeric>
using namespace std;
#define int long long 
#define LL long long
#define ios  ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define inf 1e18
#define INF 1e18
#define eps 1e-6
#define mem(a,b) memset((a),(b),sizeof(a))
const int maxn=2e5+10;
const int mod=1e9+7;
int dp[maxn][2][2];
int n;
int a[maxn],b[maxn];
signed main ()
{
  cin>>n;
  for (int i=1;i<=n;i++)
  {
    cin>>a[i];
  }
  for (int i=1;i<=n;i++)
  {
    cin>>b[i];
  }
  for (int i=0;i<=n;i++)
  {
    for (int x=0;x<=1;x++)
    {
      for (int y=0;y<=1;y++)
      {
        dp[i][x][y]=inf;
      }
    }
  }
  dp[1][1][1]=0;
  dp[1][0][0]=a[1];
  for (int i=2;i<=n;i++)
  {
    dp[i][1][0]=min(dp[i-1][1][0]+b[i-1],dp[i-1][0][0]);//点i和点i-1在同一个集合，需要删除边
    dp[i][1][1]=min(dp[i-1][1][1]+b[i-1],dp[i-1][0][1]);
    dp[i][0][0]=min(dp[i-1][0][0]+b[i-1]+a[i],dp[i-1][1][0]+a[i]);//还要记得防止i和0在同一个集合
    dp[i][0][1]=min(dp[i-1][0][1]+b[i-1]+a[i],dp[i-1][1][1]+a[i]);
  }
  int ans=inf;
  for (int i=0;i<=1;i++)
  {
    for (int j=0;j<=1;j++)
    {
      if(i==j)
      {
        ans=min(ans,dp[n][i][j]+b[n]);
      }
      else 
      {
        ans=min(ans,dp[n][i][j]);
      }
    }
  }
  cout<<ans<<"\n";
  system ("pause");
  return 0;
}

G(字符串，二分)

G

这个题大意是给出一个字符串，里面的字符只有\(Y\)和\(.\)两种，我们最多可以交换位置\(i\)和\(i+1\)的字符\(k\)次，问我们可以得到的最长连续\(k\)的长度

类似于学校校赛的一道题

我们可以把每一个我们需要的\(Y\)按顺序排起来需要交换的次数，记录在\(g\)数组里面

我们按照第一个\(Y\)在位置\(0\),第二个在位置\(1\),以此类推

我们每次选择让\(l\)到\(r\)这一区间的\(Y\)都放在一起，但是由于这些都可能没有在一起，贪心的想，可以让中间的那一个\(Y\)不需要动，它左边的往右边移动，它右边的往左边移动。

但是我们需要移动多少次呢

其实，我前面记录的每一个\(Y\)到相应位置的交换次数都是相对的，如果已经固定了一个应该要到的位置，不管到了哪个位置，最后相邻的都是\(Y\)，那么要让\(x\)和\(y\)个\(Y\)距离合适（要么为\(1\),要么为\(2\)...),为\(g[y]-g[x]\)

然后对以区间\(l\)到\(r\)之间的\(Y\)都连在一起了，我们贪心的想，让中间位置的\(Y\)不动，按照前面的想法，在慢慢来写

具体可以这样计算

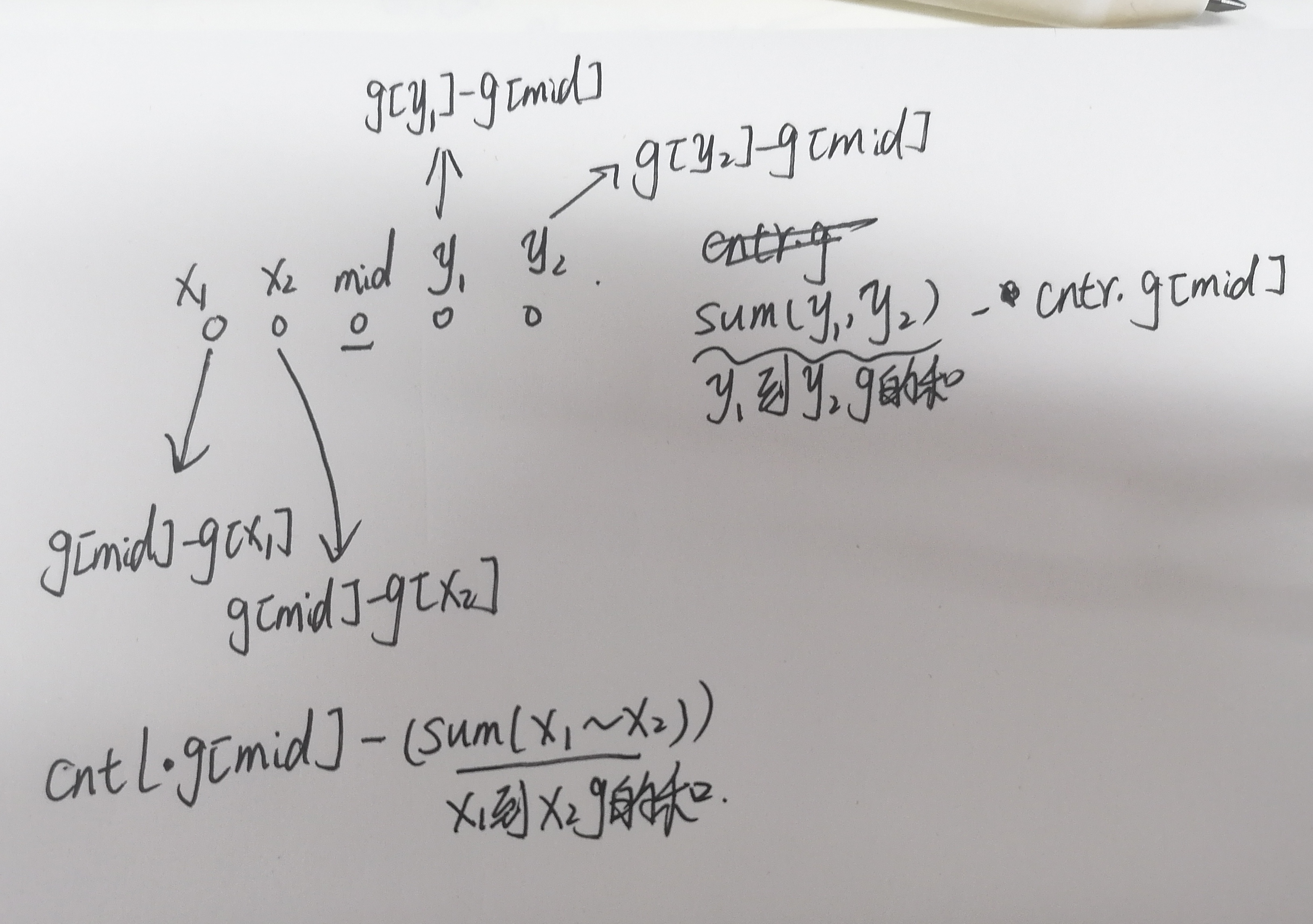
所以，我们还需要记录一下\(g\)的前缀和，然后再按照不同的长度进行二分，只要该长度每一个可以在\(k\)个操作内可以得到，那么就是可以

#include <iostream>
#include <algorithm>
#include <vector>
#include <string>
#include <map>
#include <set>
#include <queue>
#include <stack>
#include<cmath>
#include <unordered_map>
#include <array>
#include <cstring>
#include <bitset>
#include <numeric>
using namespace std;
#define int long long 
#define LL long long
#define ios  ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define inf 1e18
#define INF 1e18
#define eps 1e-6
#define mem(a,b) memset((a),(b),sizeof(a))
const int maxn=2e5+10;
const int mod=1e9+7;
int g[maxn],sum[maxn];
int n,k;
string s;
int cnt;
int fun(int l,int r)
{
  int mid=(l+r)>>1;
  int cntl=mid-l;
  int cntr=r-mid;
  int ll=cntl*(g[mid])-(sum[mid]-sum[l]);//l到mid-1
  int rr=sum[r+1]-sum[mid+1]-cntr*g[mid];
  int res=ll+rr;
  return res;
}
bool check(int len)
{
  for (int i=0,j;i+len-1<cnt;i++)
  {
    int l=i;
    int r=l+len-1;
    if(r>=cnt) break;
    int now=fun(l,r);
    if(now<=k) return true;
  }
  return false;
}
signed main ()
{
  cin>>s>>k;
  n=s.size();
  s=" "+s;
  for (int i=1;i<=n;i++)
  {
    if(s[i]=='Y')
    {
      g[cnt]=i-cnt;
      cnt++;
    }
  }
  for (int i=1;i<=cnt;i++)
  {
    sum[i]=sum[i-1]+g[i-1];
  }
  int l=1,r=cnt;
  int ans=0;
  while (l<=r)
  {
    int mid=(l+r)>>1;
    if(check(mid))
    {
      ans=mid;
      l=mid+1;
    }
    else 
    {
      r=mid-1;
    }
  }
  cout<<ans<<"\n";
  system ("pause");
  return 0;
}