AtCoder Beginner Contest 248(D,E,F)
AtCoder Beginner Contest 248(D,E,F)
D (思维,二分)
这个题大意就是给你\(n\)个数,然后有\(q\)次询问,问\(l\)到\(r\)这个区间等于\(x\)的数有多少个
这个我之前想过用树状数组,每一个数都会建一颗数,但是我发现这不现实
后来看了题解,发现一个了一个的很好的办法
它也是为每一个数都创建一个东西,但不是数,而是一个\(vector\),里面存的是这个数的位置,因为我们是正序遍历的,那么这个数组里面的数也是有序的,然后我们要求这个范围里面的这个数有多少个,不妨转化为这一个数有多少个位置是在这个范围里面的,刚好,每一个数我们都把他的位置有序的保存下来了,所以我们就直接可以\(upper__bound-lower__bound\)了
#include <iostream>
#include <algorithm>
#include <vector>
#include <string>
#include <map>
#include <set>
#include <queue>
#include <stack>
#include<cmath>
#include <unordered_map>
#include <array>
#include <cstring>
using namespace std;
#define int long long
#define LL long long
#define ios ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define inf 1e18
#define INF 1e18
#define mem(a,b) memset((a),(b),sizeof(a))
const double eps=1e-9;
const int maxn=2e5+10;
int n,q;
vector<int>x[maxn];
signed main()
{
cin>>n;
for (int i=1;i<=n;i++)
{
int num;
cin>>num;
x[num].push_back(i);
}
cin>>q;
while (q--)
{
int l,r,num;
cin>>l>>r>>num;
int ans=upper_bound(x[num].begin(),x[num].end(),r)-lower_bound(x[num].begin(),x[num].end(),l);
cout<<ans<<"\n";
}
system ("pause");
return 0;
}
E (几何,组合问题,容斥)
这个题大意就是给你\(n\)个点,任意\(k\)个点可以组成多少条直线
但是这个题我们还要特判一下,如果\(k\)是\(1\)的话,那么就有无限个点了,直接输出
首先我们要知道两点之间一定有一条直线,我们可以先固定这一条直线,然后再来寻找这一条直线里面还有多少其实的点
但是对于一条直线上的,如果存在\(cnt\)个点,那么它就会用来计算\(\frac{cnt\times (cnt-1)}{2}\)次,当实际上我们只要计算一次即可,所以,对于我们记录已有的答案\(cnt\)时,还需要除去那些多计算的次数
还有,我们需要知道怎么判断这三个点是否在一条直线上
假设点\(a\)为\((x1,y1)\),点\(b\)为\((x2,y2)\),点\(c\)为\((x3,y3)\)
如果上面这个\(flag\)等于\(0\),那么这三个点共线
#include <iostream>
#include <algorithm>
#include <vector>
#include <string>
#include <map>
#include <set>
#include <queue>
#include <stack>
#include<cmath>
#include <unordered_map>
#include <array>
#include <cstring>
using namespace std;
#define int long long
#define LL long long
#define ios ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define inf 1e18
#define INF 1e18
#define mem(a,b) memset((a),(b),sizeof(a))
const double eps=1e-9;
const int maxn=2e5+10;
int n,k;
int cnt[maxn];
struct node
{
int x,y;
}a[maxn];
bool check(int i,int j,int k)
{
int tx1=a[i].x-a[j].x,tx2=a[i].x-a[k].x;
int ty1=a[i].y-a[j].y,ty2=a[i].y-a[k].y;
if(tx1*ty2==tx2*ty1) return true;
return false;
}
signed main()
{
cin>>n>>k;
for (int i=1;i<=n;i++)
{
cin>>a[i].x>>a[i].y;
}
if(k==1)
{
cout<<"Infinity\n";
system ("pause");
return 0;
}
for (int i=1;i<=n;i++)
{
for (int j=i+1;j<=n;j++)
{
int res=2;
for (int k=1;k<=n;k++)
{
if(i==k||j==k) continue;
if(check(i,j,k))
{
res++;
}
}
cnt[res]++;
}
}
int ans=0;
for (int i=k;i<=n;i++)
{
int tmp=i*(i-1)/2;
ans=ans+cnt[i]/tmp;
}
cout<<ans<<"\n";
system ("pause");
return 0;
}
F(dp)
这个题题我是这样理解的,给你\(n\),然后会有一个\(2\times n\)的点,这些点最开始都会和他们相邻的点连接,问有多少个方式删除\(i\)个边后,这些点都还是连通的
对于这一个题,我们可以设计一个状态\(dp[i] [j] [k]\),代表前\(i\)个点,删除了\(j\)个点,其连通性是\(k\).(\(0\)是非连通,\(1\)是连通)
然后对于状态之间的转移,我们有以下规律
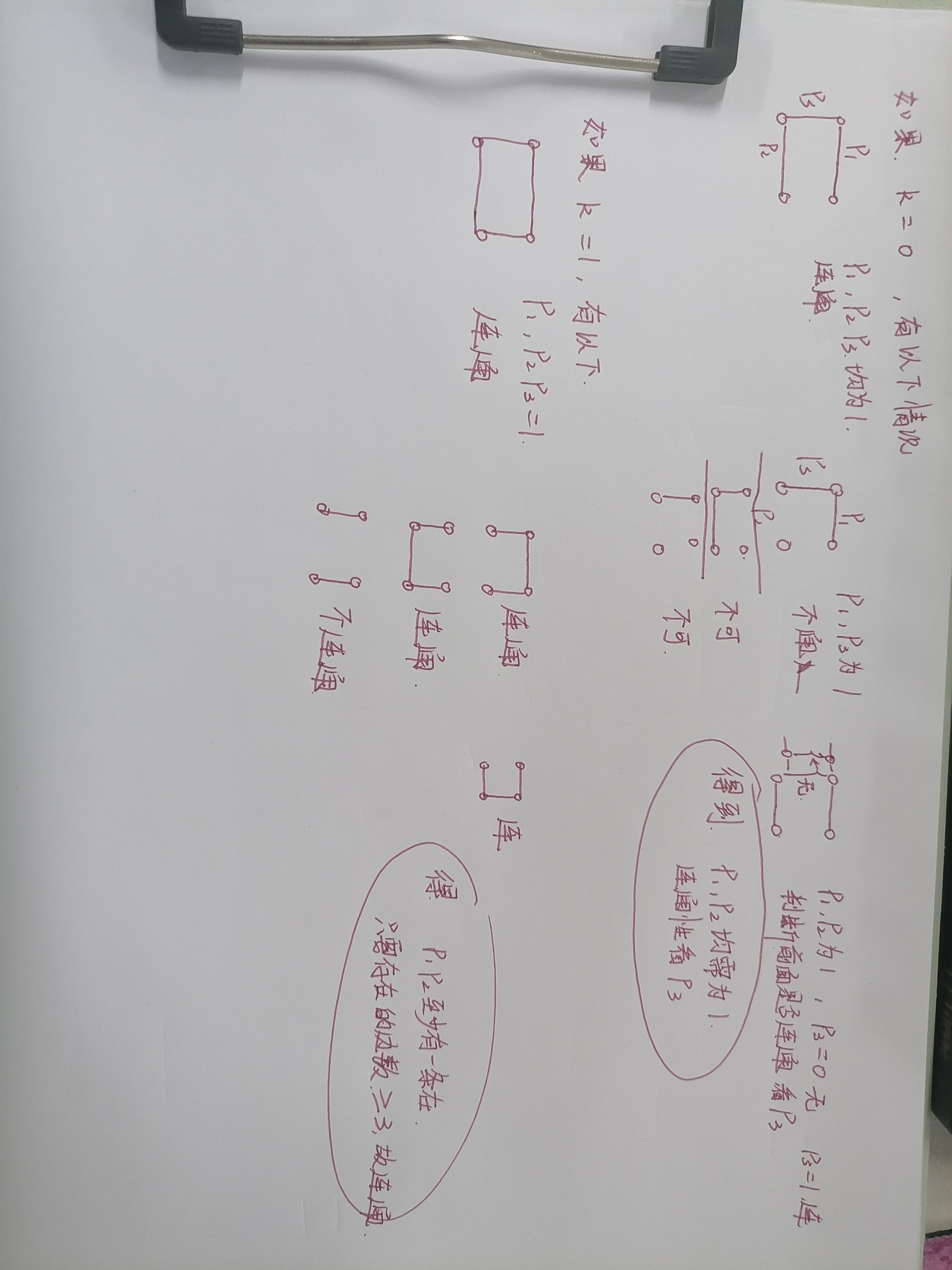
然后我们就可以很轻松的得到状态转移方程
for (int p1=0;p1<2;p1++)
{
for (int p2=0;p2<2;p2++)
{
for (int p3=0;p3<2;p3++)
{
if(k==0)//p1,p2是邻边,p3是对边,如果这一条边没有连接,要想保持连通性,两个邻边必须都存在
{
if(p1==0||p2==0) continue;
int nxtj=j+1-p3;
add(dp[i+1][nxtj][p3],dp[i][j][k]);
}
else if(k==1)//p1,p2至少有一个,要连通
{
if(p1==0&&p2==0) continue;
int nxtj=j+3-(p1+p2+p3);
int nxtk=(p1+p2+p3)>=2;
add(dp[i+1][nxtj][nxtk],dp[i][j][k]);
}
}
}
}
然后在这一道题的初状态我还有了一个更新理解(我之前可能还是一知半解),对于初状态,并不意味它一定是我们可以选择的,但是一定可以存在的
如这个题的初状态,\(dp [0] [1] [0]\),对于删除了一条边之后,它一定是不连通的,这个状态是存在的,\(dp [0] [0] [1]\),对于没有删除了一条边,它一定是连通的,这个状态是存在的,而且都只有一种方式
感觉说了又好像没说,感觉这个看个人的理解吧
而且,我在这里第一次使用了\(add\),我发现取模运算比起加减运算,时间效率不高,反正,取模的时间效率比起其他一般的运算都比较低。难怪好多次看到其他人的代码里面有这个,还有之前求奇偶数也不是用取模,而是且运算,看来是这样的
#include <iostream>
#include <algorithm>
#include <vector>
#include <string>
#include <map>
#include <set>
#include <queue>
#include <stack>
#include<cmath>
#include <unordered_map>
#include <array>
#include <cstring>
using namespace std;
#define int long long
#define LL long long
#define ios ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define inf 1e18
#define INF 1e18
#define mem(a,b) memset((a),(b),sizeof(a))
const double eps=1e-9;
const int maxn=3000+10;
int n,mod;
int dp[maxn][maxn][2];
void add(int &x,int v)
{
x+=v;
if(x>mod)
{
x-=mod;
}
return ;
}
signed main()
{
cin>>n>>mod;
dp[0][1][0]=1;
dp[0][0][1]=1;
for (int i=0;i<n;i++)
{
for (int j=0;j<n;j++)
{
for (int k=0;k<2;k++)
{
if(dp[i][j][k]==0) continue;
for (int p1=0;p1<2;p1++)
{
for (int p2=0;p2<2;p2++)
{
for (int p3=0;p3<2;p3++)
{
if(k==0)//p1,p2是邻边,p3是对边,如果这一条边没有连接,要想保持连通性,两个邻边必须都存在
{
if(p1==0||p2==0) continue;
int nxtj=j+1-p3;
add(dp[i+1][nxtj][p3],dp[i][j][k]);
}
else if(k==1)//p1,p2至少有一个,要连通
{
if(p1==0&&p2==0) continue;
int nxtj=j+3-(p1+p2+p3);
int nxtk=(p1+p2+p3)>=2;
add(dp[i+1][nxtj][nxtk],dp[i][j][k]);
}
}
}
}
}
}
}
for (int i=1;i<n;i++)
{
cout<<dp[n-1][i][1]<<" ";
}
system ("pause");
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号