Codeforces Round 752 (Div. 2)（C，D，E）

Codeforces Round 752 (Div. 2)（C，D，E）

C

C

这道题的大意就是给你\(n\)个数，然后我们可以选择第\(i\)个数，如果\(a_i%(i+1)!=0\),我们就可以删除这一个数，每次删除之后每一个数的下标都会更新，然后问我们是否可以把这\(n\)个数都删除

对于每一个数，我们可能有这些数成为他们的下标，对于\(i\),从\(2\)到\(i+1\)都可能成为这个数的下标，然后我一开始觉得直接模拟就会爆掉，其实不然，因为\(lcm(2,3,4,5...32)>1e9\)，所以我们最多枚举到\(30\)多就可以了

然后我们就直接判断从\(2\)到\(i+1\)是否存在不可整除的数，如不存在就一定删除不了

#include <iostream>
#include <algorithm>
using namespace std;
#define int long long 
const int maxn=1e5+10;
int t,n;
int a[maxn];
void solve()
{
    cin>>n;
    bool can=true;
    for (int i=1;i<=n;i++)
    {
        cin>>a[i];
        bool yes=false;
        for (int j=2;j<=i+1;j++)
        {
            if (a[i]%j)
            {
                yes=true;
                break;
            }
        }
        if (!yes) can=false;
    }
    if (can)
    {
        cout<<"YES\n";
    }
    else cout<<"NO\n";
    return ;
}
signed main ()
{
    cin>>t;
    while (t--)
    {
        solve();
    }
    system ("pause");
    return 0;
}

D

D

这个虽然做出来了，但是还想记录一下

题目给我们两个数，\(x\)和\(y\),求找到一个\(n\)，满足\(n%x=y%n\)

这个可以分类讨论

如果\(x==y\),\(n=x\),那么\(n%x=y%n=0\)

如果\(x>y\),那么\(n=x+y\),那么\(n%x=y\),\(y%(x+y)=y\)

如果\(x<y\)

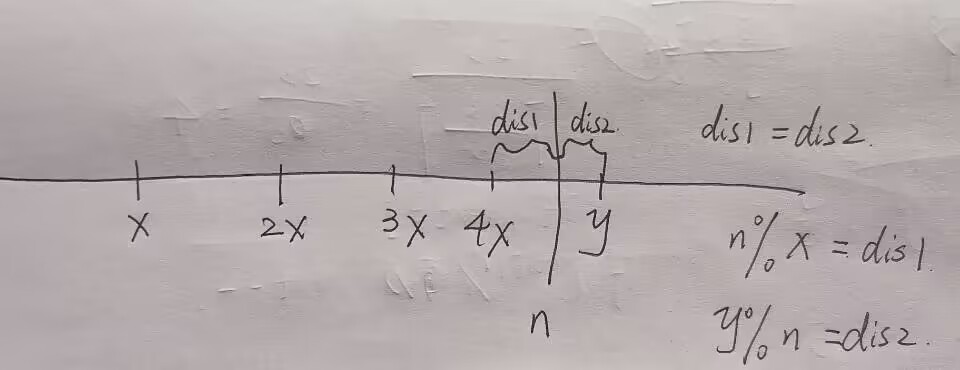
然后我们就可以写代码了

#include <iostream>
#include <algorithm>
using namespace std;
#define int long long 
int t,n;
void solve()
{
    int x,y;
    cin>>x>>y;
    int ans;
    if (x==y)
    {
        ans=x;
    }
    else if (x>y)
    {
        ans=x+y;
    }
    else 
    {
        int p=x;
        x=y/x;
        x=x*p;
        ans=(x+y)/2;
    }
    cout<<ans<<'\n';
    return ;
}
signed main ()
{
    cin>>t;
    while (t--)
    {
        solve();
    }
    system ("pause");
    return 0;
}

E

E

这个题大意是给你\(n\)个数，然后我们我们选择这\(n\)个数里面的子数组，可以选择一个数\(k\),把\(a_k\)变成\(x\)和\(y\),满足\(x+y=a_k\),使得这个子数组变成非递减的数组，每一个最后得到的非递减数组经历了\(x\)次操作，然后就得到一个价值\(x\)，问这\(n\)个数可以得到多少价值

因为我们要满足是非递减数组，所以我们可以根据后面的，得到前面的

对于此时的\(a_i\),然后我们可以根据以\(a_i\)这个位置可以得到前面一个位置的数可以是什么

比如此时以\(a_{i+1}\)为结尾的，那么我们选择在这个\(a_{i+1}\)的前面的那一项的大小可以是多少

我们要满足这个数是满足小于等于\(a_{i+1}\)，那么它前面的那些数比\(a_{i+1}\)小的

我们可以得到此时的\(cur\)，我们还可以得到上一轮的得到最前面的值为\(cur\)的分配方法\(dp[i-1] [cur]\),然后\(i\)的使用程度是\(i\)次，（如对于\((1,i+1),(2,i+1)...(i,i+1)\)),然后我们还需要把\(a_i\)分成\(v\)堆的操作数（\(v-1\)),

我们要求的是满足要求的子数组的价值和

所以我们对于分开\(a_i\)的贡献为到达这一种子数组的子数组数量乘以这一实现这一个子数组的操作数然后乘以他们每一个位置的使用程度

那么

我们可以得到每一种分开方式的贡献

\[ans=ans+i\times dp[i-1][cur]\times(v-1) \]

然后这些数组的转移还需要考虑

对于此时的\(a_i\)变成若干个\(cur\)，但是\(a_i%cur\)不一定能整除

所以对于在\(a_{i+1}\)的前面的那些数的排列可能是\(cur-1 ,cur-1,cur,cur\)这种的

所以我们还需要判断在这种分配方式的最前面的那一个数是\(a[i]/v\)

可以得到状态转移方程为

\[dp[i][next]+=dp[i-1][cur] \]

但是由于这个题的\(n\)有点大，开二维空间不够

所以我们这里使用了二进制的变化来代表此时的\(dp\)和前一轮的\(dp\)值，实际上我们也只需要这两个\(dp\)值

然后具体看代码

#include <iostream>
#include <algorithm>
using namespace std;
#define int long long 
const int maxn=1e5+10;
const int mod=998244353;
int t,n;
int a[maxn];
int dp[2][maxn];
void solve()
{
    cin>>n;
    for (int i=1;i<=n;i++)
    {
        cin>>a[i];
    }
    int ans=0;
    dp[n&1][a[n]]=1;//初始条件a[n]
    int now=n&1;
    for (int i=n-1;i>=1;i--)//a[n]是不需要变化的，（变化就变小了），往前遍历
    {
        for (int j=1;j<=a[i+1];)//cur a[i+1]，cur有多少种，这个是从最大的往小的来
        {
            int cur=a[i+1]/j;//cur a[i+1]这样的排列
            int u=dp[now][cur];//到达cur有多少种办法
            int v=(a[i]+cur-1)/cur;//v是最后分成了多少堆，那么我们需要v-1次操作
            int next=a[i]/v;// next next ,cur cur，next是最左边的状态
            ans=(ans+i*u%mod*(v-1)%mod)%mod;//对于cur a[i+1]，有i种组合，(1,i+1),(2,i+1)....(i,i+1)
            dp[now^1][next]+=u;//cur到next的方式又加多了u种
            dp[now][cur]=0;
            j=a[i+1]/cur+1;//下一种cur，cur递降
        }
        dp[now^1][a[i]]++;//以a[i]直接作为结尾
        now^=1;
    }
    cout<<ans<<'\n';
    for (int i=1;i<maxn;i++)//记得重新变成0，下一轮才不会出错
    {
        dp[0][i]=dp[1][i]=0;
    }
    return ;
}
signed main ()
{
    cin>>t;
    while (t--)
    {
        solve();
    }
    system ("pause");
    return 0;
}