【题解】CF1852 合集
CF1852A Ntarsis' Set
考虑我们先手模一下样例：
???一脸疑惑，有什么规律吗？真有，但是很难看出来捏。
正难则反，我们考虑如果知道操作一次后一个数的位置，我们可以很容易推出，操作之前它的位置：
你考虑如果最后的答案比较小的话还可以用一个数组存下每次操作前的位置。
但是，显然最后的答案很大，我们必须找到规律。
我们假设在操作后的序列中是第 \(i\) 个，操作前是第 \(j\) 个，那么一定满足 \(\forall k\leq j-i,a_k \leq j\) 在这个情况下每次让 \(j\) 最大即可，具体方法可以看 e.g / code。
e.g.
以第二个测试点为例:最后一次操作时，操作数组为 \([1, 3, 5, 6, 7]\)，\(ans\) 的位置为 \(1\)。遍历操作数组，操作数组中第一个元素 \(1 = 1\)，所以将 \(ans\) 的位置向后移动，变为 \(2\)。继续遍历，发现操作数组中第二个元素 \(3 > 2\)，已经不能继续将 \(ans\) 往后移动，那么第二次操作后在第 \(1\) 个位置的数，第二次操作前在第 \(2\) 个位置
倒推倒数第二次操作时，\(ans\) 的位置为 \(2\)。遍历操作数组，操作数组中第一个元素为 \(1 < 2\)，将 \(ans\) 位置后移至 \(3\)。继续遍历，操作数组中第二个元素为 \(3 = 3\)，将 \(ans\) 位置后移至 \(4\)。继续遍历，操作数组中第三个元素为 \(5 > 4\)，那么第一次操作后在第 \(2\) 个位置的数，操作前在第 \(4\) 个位置
倒推倒数第三次操作的方法相同，最后 \(ans\) 的位置变为 \(9\)，即为答案。
具体可以看code（代码中二分没有必要）：
#include<bits/stdc++.h> using namespace std; typedef long long ll; const int NN = 2e5 + 8; int T; int n,k; ll lft; int a[NN]; ll erf(ll x){ ll l = lft,r = n,ans = lft; while(l <= r){ int mid = (l + r) / 2; if(a[mid] <= x) ans = mid,l = mid + 1; else r = mid - 1; } return ans; } int main(){ scanf("%d",&T); while(T--){ scanf("%d%d",&n,&k); for(int i = 1; i <= n; ++i) scanf("%d",&a[i]); ll now = 1,get = 0,pre = 0; lft = 0; for(int i = 1; i <= k; ++i){ get = pre = 0; while(pre != (get = erf(now + get))) pre = get,lft = max(lft,get); now += pre; } printf("%lld\n",now); } }
CF1852B Imbalanced Arrays
标签：思维题 \(B\)
我们假设当前出长度为 \(len\)，那么我们在序列中一定有一个 \(len/0\)，因为一定有一个绝对值最大的数，如果这个数是正数在原序列中就是 \(len\)，是负数在原序列中即为 \(0\)。
由上文，我们可以得到，一定不能有 \(len\) 和 \(0\) 同时出现的情况，也一定不能有 \(len\) 和 \(now\) 都不能出现的情况。
通过这个性质，我们就可以得到下面的解法：
- 如果序列中有一个值为 \(len\) 的数，那么它一定和所有数的和都为正数，我们可以直接将它去掉，然后其它数 \(-1\)，这样我们就可以得到一个长度为 \(len-1\) 的序列。
- 如果序列中有一个值为 \(0\) 的数，那么它一定和所有数的和都为负数，我们可以直接将它去掉，这样我们也可以得到一个长度为 \(len-1\) 的序列。
- 而若序列中既没有 \(len\) 也没有 \(0\)，或 \(len\) 和 \(0\) 都有，那么一定是无解的
通过这种方法我们就可以判断能否构造出一种解。
而构造解的方法也很简单：
- 数值：让删的数的绝对值，从大到小即可（\(n \to 1\)）
- 符号：如果删的是 \(len\)，则为正数；如果删的是 \(0\)，则为负数。
code：
#include<bits/stdc++.h> using namespace std; const int NN = 1e5 + 8; typedef long long ll; struct Num{ int val,pos; bool operator < (const Num &x){ return val > x.val; } }a[NN]; int T,n,hf; int ans[NN]; ll pre[NN]; bool check(){ int head = 1, tail = n; int cnt = 0; for(int i = 1; i <= n; ++i){ if(a[tail].val == cnt && (n-i+1) - a[head].val + cnt == 0) return false; if(a[tail].val == cnt) { ans[a[tail].pos] = - (n-i+1); --tail; } else if((n-i+1) - a[head].val + cnt == 0){ ans[a[head].pos] = (n-i+1); ++head,++cnt; } else return false; } return true; } int main(){ scanf("%d",&T); while(T--){ scanf("%d",&n); for(int i = 1; i <= n; ++i) scanf("%d",&a[i].val),a[i].pos = i; sort(a+1,a+1+n); hf = -1; for(int i = 1; i <= n; ++i) pre[i] = pre[i-1] + a[i].val; if(!check()){puts("NO");continue;} puts("YES"); for(int i = 1; i <= n; ++i) printf("%d ",ans[i]); puts(""); } }
CF1852C Ina of the Mountain
标签：思维题 \(B^+\)
我们先从题目的一部分入手。
如果说，我们没有当一个数为 \(0\) 时，让这个数变成 \(k\) 的性质，我们如何求答案呢？
很简单，在图上就是：
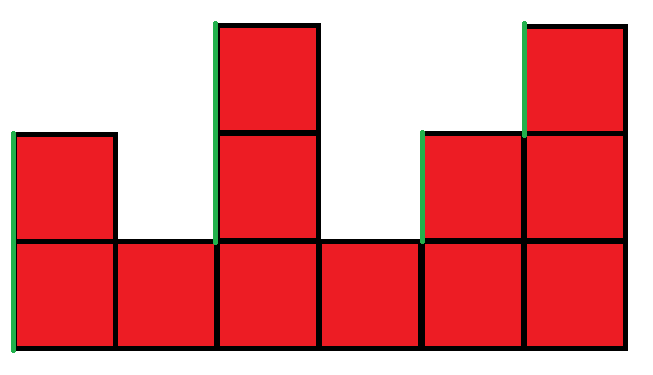
绿色线段的长度加起来即为答案（本图中是 \(6\)）
我们考虑很显然地，将一个数从 \(0\) 变为 \(k\) 即为将一个数一开始加上 \(k\)
我们如果要让第 \(i\) 列格子前面的数的代价减小，那么一定会在 \(i\) 前面找一个 \(j\) 让 \([j,i-1]\) 的区间内的所有数都加上 \(k\)，而代价为 \(a_j+k - a_{j-1}\) 我们只需要将所有的 \(a_j+k-a_{j-1}\) 放进优先队列里面，每次取最小的，和现在的\(a_i-a_{i-1}\) 取 \(\min\) 即可。
code：
#include<bits/stdc++.h> using namespace std; typedef long long ll; const int NN = 2e5 + 8; int n,k; ll a[NN]; void solve(){ scanf("%d%d",&n,&k); for(int i = 1; i <= n; ++i) scanf("%lld",&a[i]),a[i] %= k; a[n+1] = 0; priority_queue<ll, vector<ll>, greater<ll> > q; while(!q.empty()) q.pop(); ll ans = 0; for(int i = 1; i <= n + 1; ++i){ if(a[i - 1] == a[i]) continue; if(a[i - 1] > a[i]) q.push(a[i] + k - a[i - 1]); else{ q.push(a[i] - a[i - 1]); ans += q.top(); q.pop(); } } printf("%lld\n",ans); } int T; int main(){ scanf("%d",&T); while(T--) solve(); }
CF1852D Miriany and Matchstick
考虑 dp，设 \(f_{i,0/1}\) 表示考虑到前 \(i\) 位，且第 \(i\) 位填入 A/B 可能的答案集合，显然地朴素转移时间复杂度 \(O(n^2)\)。
试分析 dp 性质，观察发现所有 dp 中得到的集合为区间内抠去至多一个点。
证明
我们首先来观察转移过程是怎样的。第一种是第二行中 $i-1$ 填入的字母与第一行中 $i$ 填入的字母相同的情况，此时根据我们填入的字母与其相同与否，集合会整体平移 $0$ 或 $2$；第二种是不同的情况，此时无论我们如何填入字母，集合都会整体平移 $1$。由于我们只关心集合的相对位置关系，我们可以将转移视为将 $f_{i-1,0/1}$ 固定不动，将 $f_{i-1,1/0}$ 平移 $1$ 以及 $-1$，分别进行取或操作，得到 $f_{i}$。首先容易发现，\(f_i\) 的两个集合两侧端点的差的绝对值分别不超过 \(2\)。这是由于这两个集合是由一个固定的集合或上另外一个集合平移 \(1/-1\) 得到的。现在，我们可以归纳说明一个更强的结论：\(f_i\) 的两个集合中至多存在一个集合中存在且恰存在一个空位。
显然 \(1\) 满足条件。假设 \(i-1\) 满足此条件。由于区间过小时的情况比较神秘，我们在此只讨论 \(r-l+1\ge5\) 的情况。对于区间更小的情况打表可证。在这种情况下，最坏是 \(f_{i-1,x}\) 为 \([l,r]\) 抠去 \(p(p\in(l,r))\)，\(f_{i-1,1-x}\) 为 \([l+2,r-2]\)。此时，若 \(i\) 不满足此条件，则存在一个 \(p\) 使得 \([l+2,r-2]\) 无论平移 \(1\) 还是 \(-1\) 都无法覆盖到，而这显然无解。
故证毕。证得比原结论更强的结论，故原结论也证毕。
褐自落谷题解
所以说对于每个 \(f_{i,0/1}\) 只需要维护 \((l,r,p)\)，即（左端点，右端点，中间挖去的点）
时间复杂度 \(O(n)\)。
code：
#include<bits/stdc++.h> using namespace std; const int NN = 2e5 + 8; int T; int n,k; char s[NN],S[NN]; struct Node{ int l,r,p; Node operator + (int x){ return {l+x,r+x,p==-1?-1:p+x}; } bool ckin(int x){ return l <= x && x <= r && x != p; } }f[NN][2]; Node operator ^ (Node a, Node b){ if(a.l > b.l) swap(a,b); Node res = {min(a.l,b.l),max(a.r,b.r),-1}; if(a.r + 2 == b.l) res.p = a.r + 1; else{ if(a.p != -1 && !b.ckin(a.p)) res.p = a.p; if(b.p != -1 && !a.ckin(b.p)) res.p = b.p; } return res; } int main(){ scanf("%d",&T); while(T--){ scanf("%d%d",&n,&k); scanf("%s",s+1); for(int i = 1; i < n; ++i) k -= (s[i]!=s[i+1]); if(k < 0){puts("NO");continue;}//判第一行 int type = s[1] - 'A'; f[1][type^1] = {1,1,-1}; f[1][type] = {0,0,-1}; int ty; for(int i = 2; i <= n; ++i){ ty = s[i]-'A'; f[i][ty] = f[i-1][ty] ^ f[i-1][ty^1]+1; f[i][ty^1] = f[i-1][ty]+2 ^ f[i-1][ty^1]+1; } ty = -1; if(f[n][0].ckin(k)) ty = 0; if(f[n][1].ckin(k)) ty = 1; if(ty == -1) {puts("NO");continue;} puts("YES"); for(int i = n; i; --i){ S[i] = 'A' + ty; if(i == 1) break; k -= (S[i]!=s[i]); if(f[i-1][ty].ckin(k)) continue;//只要有答案就走 ty ^= 1, --k; } printf("%s\n",S+1);//ans collecting for(int i = 1; i <= n; ++i) S[i] = '\000'; } }
本文来自博客园，作者：ricky_lin，转载请注明原文链接：https://www.cnblogs.com/rickylin/p/CF1852.html
【推荐】国内首个AI IDE，深度理解中文开发场景，立即下载体验Trae
【推荐】编程新体验，更懂你的AI，立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包，你的智能百科全书，全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell：AI 加持，快人一步
· 阿里最新开源QwQ-32B，效果媲美deepseek-r1满血版，部署成本又又又降低了！
· 开源Multi-agent AI智能体框架aevatar.ai，欢迎大家贡献代码
· Manus重磅发布：全球首款通用AI代理技术深度解析与实战指南
· 被坑几百块钱后，我竟然真的恢复了删除的微信聊天记录！
· AI技术革命，工作效率10个最佳AI工具