【题解】CF1817 合集

CF1817A Almost Increasing Subsequence

标签：思维题 \(C\)

考虑几乎上升的序列的长度，就是我们的区间长度减去 \(a_{i-2} \geq a_{i-1} \geq a_i\) 的对数，然后维护即可，当然个人感觉自己的代码有点长，可以考虑看洛谷题解代码

code:

#include<bits/stdc++.h>
using namespace std;
const int NN = 2e5 + 8;
int n,q;
int a[NN];
int pre[NN],cnt[NN],ck[NN];
int main(){
//	freopen("1.out","w",stdout);
	scanf("%d%d",&n,&q);
	for(int i = 1; i <= n; ++i) scanf("%d",&a[i]);
	for(int i = 1; i <= n; ++i){
		if(i < n && a[i] >= a[i+1]) pre[i] = 1,ck[i] = 1;
		if(i < n && a[i] >= a[i+1] && a[i-1] < a[i]) cnt[i] = 1;
		pre[i] += pre[i-1];
		cnt[i] += cnt[i-1];
	}
//	for(int i = 1; i <= n; ++i) printf("%d ",pre[i]);puts("");
//	for(int i = 1; i <= n; ++i) printf("%d ",cnt[i]);puts("");
	while(q--){
		int l,r;
		scanf("%d%d",&l,&r);
		if(l == r){puts("1");continue;}
		if(l == r-1){puts("2");continue;}
		printf("%d\n",(r-l+1) - (pre[r-1] - pre[l-1]) + (cnt[r-1] - cnt[l] + ck[l]));
	}
}

CF1817B Fish Graph

标签：图论 \(B^-\) | 思维题 \(B^-\)

我们的目的就是找到一个环，且环上的其中一个点至少和环外两个的点有边相连。

我们考虑我们肯定不能把所有的环都找一遍，这样一定会 TLE。

那么我们该怎么做呢？

我们可以发现一个性质，就是一个环上如果有度数大于等于 \(4\) 的点，那么这个点一定包含在满足要求的环内。（显然很容易证明）

我们就可以从度数大于等于 \(4\) 的点开始搜索（那么我们会有两种情况）：

  • 我们搜到了一条连向当前搜索树的根的返祖边，那么我们一定能找到一个环上只包含。时间复杂度 \(O(n^2)\)
  • 我们搜不到一条连向当前搜索树的根的返祖边，那么这个点就不在任意一条环上。时间复杂度 \(O(n)\)

因为我们只需要找到一个满足要求的环即可，所以总的时间复杂度为 \(O(n^2\times 1 + n\times n)\)，即 \(O(n^2)\)

code:

#include<bits/stdc++.h>
using namespace std;
const int NN = 2e3 + 8;
int t,n,m;
int sta[NN],top,gt;
bool vis[NN],col[NN];
int du[NN];
 
struct Edge{
	int to,next;
}edge[NN << 1];
int head[NN],cnt;
void init(){
	for(int i = 0; i <= n; ++i) head[i] = -1,vis[i] = 0,du[i] = 0;
	cnt = 1;top = 0;gt = 0;
}
void add_edge(int u,int v){
	edge[++cnt] = {v,head[u]};
	head[u] = cnt;
}
int nowu,nowv;
int eu[4],ev[4];
bool check(int u,int v){
	nowu = u;nowv = v;
	bool res = 0;
	int tp = top;
	while(sta[tp] != u) col[sta[tp--]] = 1;
	col[sta[tp]] = 1;
	tp = top;
	while(sta[tp+1] != u){
		int fm = sta[tp--],cnt = 0;
		for(int i = head[fm]; i != -1 && cnt <= 2; i = edge[i].next){
			int to = edge[i].to;
			if(!col[to]){eu[cnt] = fm;ev[cnt++] = to;}
		}
		if(cnt >= 2) {res = 1;break;}
	}
	tp = top;
	while(sta[tp] != u) col[sta[tp--]] = 0;
	col[sta[tp]] = 0;
	return res;
}
void dfs(int u,int fae,int rt){
	sta[++top] = u;vis[u] = 1;
	for(int i = head[u]; i != -1; i = edge[i].next){
		int v = edge[i].to;
		if((i^1) == fae) continue;
		if(v == rt){
			if(check(v,u)) gt = 1;
		}
		else if(!vis[v])dfs(v,i,rt);
		if(gt) {vis[u] = 0;return;}
	}
	--top;vis[u] = 0;
}
 
int main(){
	scanf("%d",&t);
	while(t--){
		scanf("%d%d",&n,&m);init();
		int rt;
		for(int i = 1,u,v; i <= m; ++i){
			scanf("%d%d",&u,&v);add_edge(u,v);add_edge(v,u);
			++du[u];++du[v];
		}
		for(int i = 1; i <= n; ++i,top = 0) {
			if(du[i] >= 4) dfs(i,-1,i);
			if(gt) break;
		} 
		if(gt){
			puts("YES");
			int tp = top,ans = 0;
			while(sta[tp] != nowu) ++ans,tp--;
			ans += 3;
			printf("%d\n",ans);
			for(int i = tp; i < top; ++i)
				printf("%d %d\n",sta[i],sta[i+1]);
			printf("%d %d\n",sta[top],sta[tp]);
			printf("%d %d\n%d %d\n",eu[0],ev[0],eu[1],ev[1]);
		}
		else puts("NO");
	}
}

CF1817C Similar Polynomials

标签：数学 \(B^+\)

多项式次数太高了，不好处理。考虑 “求导” 降次。离散意义下就是差分。

我们知道，对函数做形如 \(f'(x) \gets f(x + 1) - f(x)\) 的差分，则 \(\deg f' = \deg f - 1\)。所以将 \(d + 1\) 个点值差分 \(d - 1\) 次，\(A\) 从 \(d\) 次变成 \(1\) 次，也就是直线 \(A' = kx + b\)。

\(A(0\sim d)\) 的 \(d - 1\) 阶差分 \(a_0, a_1\) 分别等于 \(A'(0), A'(1)\)，相当于 \(kx + b\) 在 \(x = 0\) 和 \(x = 1\) 处的点值。

\(B(0\sim d)\) 即 \(A(s\sim s + d)\) 的 \(d - 1\) 阶差分 \(b_0, b_1\) 分别等于 \(A'(s), A'(s + 1)\)，相当于 \(kx + b\) 在 \(x = s\) 和 \(x = s + 1\) 处的点值。

显然，根据 \(a_0\) 和 \(a_1\) 可以直接确定直线，再代入 \((s, b_0)\) 或 \((s + 1, b_1)\) 即可。答案即 \(\frac {b_1 - a_1} {a_1 - a_0}\) 或 \(\frac {b_0 - a_0} {a_1 - a_0}\)。

至于 \(k\) 阶差分怎么求：

你考虑多项式差分的定义为：

\[\Delta f(x) = f(x+1)-f(x) \]

\[\Delta^kf(x) = \Delta^{k-1}f(x+1) - \Delta^{k-1}f(x) \]

我们可以从生成函数的角度考虑，一次差分本质上就是乘上了 \((x-1)\)，\(k\) 阶差分就是乘上了 \((x-1)^k\) 即可推出下面的式子：

\[\Delta ^ k f(x) = \sum_{i = 0} ^ k \binom k i(-1) ^ {k - i} f(x +i) \]

时间复杂度 \(\mathcal{O}(d)\)。

code:

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int NN = 3e6 + 8,MOD = 1e9 + 7; 
ll d;
ll A[NN],B[NN];
ll fac[NN],inv[NN];

ll ksm(ll x,ll k){
	ll res = 1;
	while(k){
		if(k&1) res = res * x % MOD;
		x = x * x % MOD;
		k >>= 1;
	}
	return res;
}
ll binom(ll n,ll m){
	return fac[n] * inv[m] % MOD * inv[n-m] % MOD;
}
int main(){
	scanf("%lld",&d);
	fac[0] = 1;
	for(int i = 1; i <= d; ++i) fac[i] = fac[i-1] * i % MOD;
	inv[d] = ksm(fac[d],MOD - 2);
	for(int i = d; i >= 1; --i) inv[i-1] = inv[i] * i % MOD;
	
	for(int i = 0; i <= d; ++i) scanf("%lld",&A[i]);
	for(int i = 0; i <= d; ++i) scanf("%lld",&B[i]);
	
	ll k,b,res = 0;
	for(int i = 0; i <= d-1; ++i)
		res = (res + binom(d-1,i) * ((d-1-i)&1?-1:1) * A[i]) % MOD;
	b = res;res = 0;
	for(int i = 0; i <= d-1; ++i)
		res = (res + binom(d-1,i) * ((d-1-i)&1?-1:1) * A[i+1]) % MOD;
	k = res - b;res = 0;
	for(int i = 0; i <= d-1; ++i)
		res = (res + binom(d-1,i) * ((d-1-i)&1?-1:1) * B[i]) % MOD;
	ll s = (res - b) * ksm(k,MOD - 2) % MOD;
	printf("%lld",(s+MOD) % MOD);
}

CF1817D Toy Machine

标签：思维题 \(B\)

一道很好玩的游戏题。

题目也非常良心，给了一个可以操作的网页：

2

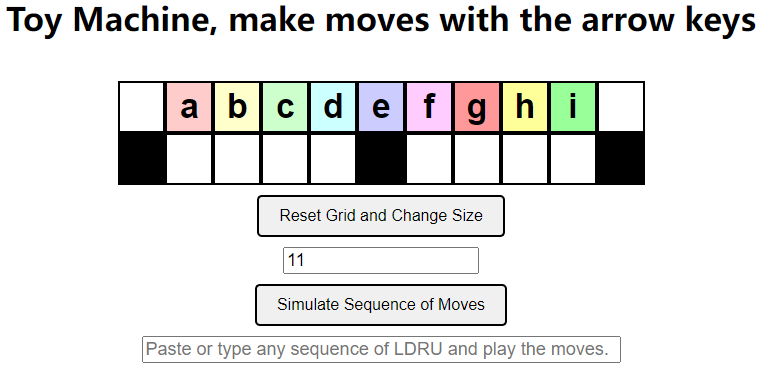
option 1：我们考虑手玩一下可以发现左半部分很简单，就是 LDRU 即可，然后最后接一个 L（下图为将 d 挪到最左边）。

2

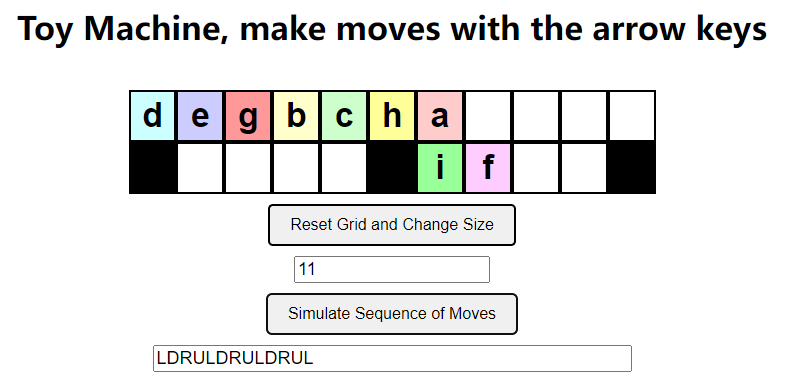
关键是右半部分怎么挪动到左边？

option 2：我们发现我们可以使用 RDRU 将所有玩具都挪到最右边，然后再用一个 L 将最右边的玩具挪到最左边

1

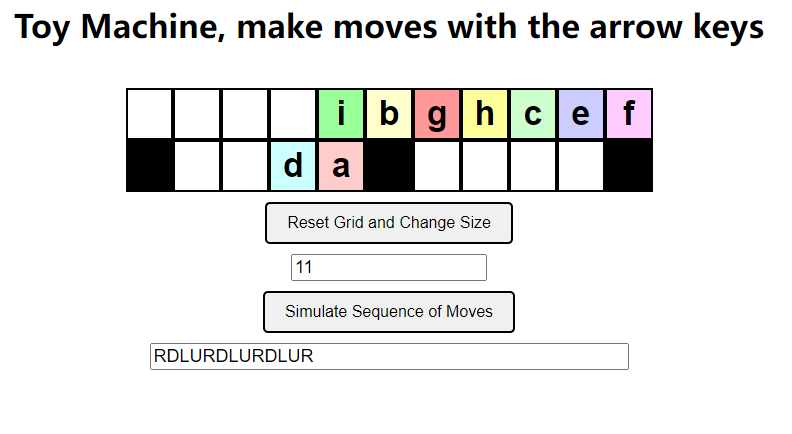
option 3：现在我们就需要将右半部分的玩具挪到最右边，可以模仿挪到最右边的方法 RDLU 即可，然后最后接一个 R（下图为将 f 挪到最右边）

1

我们的右边的玩具的挪动方法便出来了，就是先用该玩具通过 option 3 挪到最右边，再使用 option 2 将其挪到左半部分，最后使用 option 1 将其挪到最左边。

code:

#include<bits/stdc++.h>
using namespace std;
int n,k;
int main(){
	scanf("%d%d",&n,&k);
	if(k == n/2) return puts("DL"),0;
	if(k < n/2){
		for(int i = 1; i < k; ++i) printf("LDRU");//operation 1
		printf("L\n");
	}//左半边
	else{
		for(int i = k; i < n-2; ++i) printf("RDLU");//operation 3
		for(int i = 1; i <= n/2+10; ++i) printf("RDRU");//operation 2
		for(int i = 1; i < n/2; ++i) printf("LDRU");//operation 1
		printf("L");
	}//右半边
}
posted @ 2023-09-19 21:13  ricky_lin  阅读(74)  评论(0)    收藏  举报