时间复杂度相关

一，时间复杂度

 

　　

#引入问题 ！ 如何a+b+c=1000,且 a^2+b^2=c^2,（a,b,c为自然数） 则a,b,c可能的组合！
import time
'''
枚举法解决
'''
# strat_time=time.time()
# for a in range(1001):
#     for b in range(1001):
#         for c in range(1001):
#             if a+b+c==1000 and a**2+b**2 == c**2:
#                 print(a,b,c)
# end_time = time.time()
# print(end_time-strat_time)
#改进
strat_time=time.time()
for a in range(1001):
    for b in range(1001):
        c=1000-a-b
        if  a**2+b**2 == c**2:
            print(a,b,c)

end_time = time.time()
print(end_time-strat_time)

#时间复杂度 T(n)
'''
推导步骤
     x =（具体的运算步骤） 系数不影响函数的走势
     T =1000*1000*1000* x
     T=2000*2000*2000* x   n（代表的是 解决问题的规模）
     T=N*N*N*x
     T(n) = n^3*x
     T(n) = g(n)  渐近函数  忽略系数x
     T（n）= O（g（n））
     T(n)=O(f(n)), 称 O(f(n))
 严格定义：
        "大0记法”：对于单调的蝥数函数f，如果存在一个S数函致g和实常数〇0,使得对于充分大的n总有f(n） <=c*g(n>,
        就说函数g是f的一个渐近函数（忽輅常数），
        记为f(n)=0(g(n))。也就是说，在趋向无穷的极限* 义下，
        函数f的增长速度受到函数g的约束，亦即函数f与函数g的特征相似。
        
        时间S杂度：假设存在函数g,使得篝法A处理规播为n的问應示例所用时间为T(n)=0(g〇J),则称0(g(n))为 *法A的渐近吋间复杂度，简称时间复杂度，记为T<nJ

　　

二 最坏时间复杂度

　　

#引入问题 ！ 如何a+b+c=1000,且 a^2+b^2=c^2,（a,b,c为自然数） 则a,b,c可能的组合！

'''
 分析算法时.存在几种可能的考虑:
    •算法宪成工作最少需要多少基本操作，即最优时间复杂度
    •算法宪成工作最多需要多少墨本操作，即最坏时间复杂度
    •算法完成工作平均需要多少基本操作.即平均时间复杂度

    对于最优时间复杂度，其价值不大，因为它没有提供什么有用倌息.其反映的只ft最乐观最理想的情况，没 有参考价值，
    对于最坏时间霣杂度，提供了一种保证，表明算法在此种程度的®本操作中一定能完成工作，
    对于平均时间复杂度.是对算法的一个全面评价，因此它完螯全面的反映了这个算法的性质#
    但另一方面. 这种衡屋并没有保证，不*每个计算都能在这个基本操作内完成。
    而且，对于平均情况的计算，也会因为应 用算法的实例分布可能并不均匀而难以计算》
    因此，我们主要关注算法的嚴坏悄况，亦即最坏时间复杂度_

时间复杂度的几条基本计算规则
    1.	基本操作.即只有常数项，认为其时间复杂度为O(1}
    2.	顺序结构，时间复杂度按加法进行计算
    3.	循环结构（循环结构），时间复杂度按算法进行计算
    4.  分支结构（条件语句），时间复杂度取最大值	\
    5.	判断一个算法的效率时，往往只需要关注操作数量的B高次项.其它次要项和常数项可以忽略
    6.	在没有特殊说明时.我们所分析的算法的时间复杂度都是指 ‘最坏时间复杂度’
'''


import time

strat_time=time.time()
for a in range(1001):
    for b in range(1001):
        c=1000-a-b
        if a+b+c==1000 and a**2+b**2 == c**2:
            print(a,b,c)

end_time = time.time()
print(end_time-strat_time)
#计算改进后的时间复杂度
'''
T(n) =n*n*(1+max(1,0))
     = n^2*2
     =O(n^2)
'''

　　

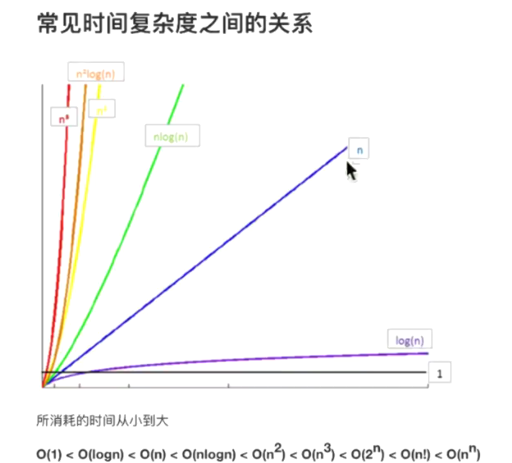
三，常见的时间复杂度与大小关系

 

　　

'''
常见时间复杂度
执行次数函数举例   阶	      非正式术语
12	               0(1)	        常数阶
2n+3	           O(n)	        线性阶
3n2+2n+1	       O(n^2)	    平方阶
5log2n+20	       O(logn)	    对数阶
2n+3nlog2n+19	   O(nlogn)	    nlogn 阶
6n3+2n2+3n+4	   O(n^3)	    立方阶
2n	               0(2^n)	    指数阶

"注意，经常将log2n (以2为底的对数）简写成logn"

'''

　　

图解：

 

 

本文作者：rianley cheng

作者QQ：2855132411

转载请注明出处！