Codeforces 766 Div.2题解
Codeforces 766 Div.2题解
A
题意:给你一个矩阵,每一次操作你可以选择一个字符为B的位置(x , y),可以使得x行字符都变为B,或者是让y行字符都变成B
现在问你什么情况下可以使 (x1,y1) 所在的位置字符为B
简单分析一下:
①当(x1,y1)就是B的时候操作次数是0次
②当矩阵中不存在B的时候,不存在答案,为-1
③当x1行或者y1列存在B,那么操作次数是1次
④否则,就需要两次,从非x1行,非y1列的地方随便操作一个B,可以使得x1行 or y1列中出现一个B,那么就变成了③的情况,答案是2
查看代码
#include<iostream>
#include <vector>
#include <cstring>
#include <map>
#include <algorithm>
using namespace std;
typedef long long ll;
const int MAXN = 55;
char a[MAXN][MAXN];
/*
4 10 1
0 3 4 8
5 8 3 6
*/
void solve()
{
int n,m,x,y;
scanf("%d %d %d %d",&n,&m,&x,&y);
int f = 0;
for(int i = 1;i <= n;++i) scanf("%s",a[i] + 1);
for(int i = 1;i <= n;++i)
for(int j = 1;j <= m;++j)
{
if(a[i][j] == 'B') {
f = 1;
break;
}
}
if(!f) {
puts("-1");
return ;
}
if(a[x][y] == 'B')
{
puts("0");
return ;
}
for(int i = 1;i <= n;++i)
if(a[i][y] == 'B') {
puts("1");
return ;
}
for(int i = 1;i <= m;++i)
{
if(a[x][i] == 'B') {
puts("1");
return ;
}
}
puts("2");
}
int main()
{
int t = 1;
scanf("%d",&t);
while(t--)
solve();
return 0;
}B
题意:
给你一个N * M的矩阵,Tina可以选择其中的k个位置(k∈[0,n * m - 1]),使得这k个位置染色成为粉色,Rahul不会坐在粉色的位置,而Tina可以坐在任何的位置上。然后Rahul和Tina轮流选择位置,Rahul想要最后同Tina坐的尽可能近,而Tina想要和他坐的尽可能远,问你若他们两个都非常聪明,k∈[0 , n * m - 1]这时候的最远距离分别是多少
分析:
①由于k是在 0 ~ n * m - 1范围之内的,那么Rahul会将所有的位置都坐一遍
②由于Tina要坐的和Rahul尽可能的远,那么最优的情况就是选择矩阵的四个角落(很简单的贪心吧)
③K越大,Tina和Rahul的距离会尽可能的远,也就是说答案是递增的
那么我们就可以将所有的位置都遍历一遍,然后和四个角的哈密顿距离进行对比,取最大的那个,最后将数组排序,输出前n * m个数字即可
查看代码
#include<iostream>
#include <vector>
#include <cstring>
#include <map>
#include <algorithm>
using namespace std;
typedef long long ll;
const int MAXN = 55;
char a[MAXN][MAXN];
/*
4 10 1
0 3 4 8
5 8 3 6
*/
vector<int> ans;
int dis(int x,int y,int x1,int y1)
{return abs(x - x1) + abs(y - y1);}
void solve()
{
ans.clear();
int n,m;
scanf("%d %d",&n,&m);
for(int i = 1;i <= n;++i)
for(int j = 1;j <= m;++j)
{
ans.push_back(max(max(dis(i,j,1,1),dis(i,j,n,m)),max(dis(i,j,1,m),dis(i,j,n,1))));
}
sort(ans.begin(),ans.end());
int siz = n * m - 1;
for(int i = 0;i <= siz;++i)
printf("%d%c",ans[i], " \n"[i == siz]);
}
int main()
{
int t = 1;
scanf("%d",&t);
while(t--)
solve();
return 0;
}C
题意:
给你一棵树,你要给所有的边添加一个权值,使得每一个长度 <= 2的路径权值和都是一个质数
分析:
我们可以直接看到第三个样例,它为什么不能够构成一个Prime树。
①分析可知,两个非2的素数进行相加操作,得到的数字一定不是质数
②如果一个节点的度为3,那么势必需要存在两个2,才可以使得其中的两条边和为质数,但是那两条2的边形成的不是质数,因此存在节点度数 >= 3的树就直接输出-1
③可以知道这颗树是一个链,我们只需要从度数为0的点开始,依次对各条边进行赋值即可(2,5,2,5,2,5,2....依次)
代码有点乱,可以看看正解的代码
查看代码
#include<iostream>
#include <vector>
#include <cstring>
#include <map>
#include <algorithm>
using namespace std;
typedef long long ll;
const int MAXN = 1e5 + 7;
bool prime[MAXN * 16 + 1];
int p[MAXN],top = 0;
/*
4 10 1
0 3 4 8
5 8 3 6
*/
vector<int> ans,tmp;
void ini()
{
top = 0;
int MAX = 1e6;
for(int i = 2;i < MAX;++i)
{
if(!prime[i]) p[++top] = i;
for(int j = 1;j <= top && 1ll * p[j] * i < MAX;++j)
{
prime[p[j] * i] = 1;
if(i % p[j] == 0) break;
}
}
}
struct node{
int x,id;
node(int x = 0,int id = 0):x(x),id(id){}
};
int deg[MAXN],a[MAXN];
vector<node> g[MAXN];
/*
1
6
3 4
4 5
5 6
2 1
2 3
*/
struct no{
int x,y,id;
}all[MAXN];
void dfs(int x,int fa,int ls)
{
for(int i = 0;i < g[x].size();++i)
{
node t = g[x][i];
if(t.x == fa) continue;
if(ls == 2)
a[t.id] = 5;
else
a[t.id] = 2;
dfs(t.x,x,a[t.id]);
}
}
void solve()
{
int n;
scanf("%d",&n);
for(int i = 1;i <= n;++i) deg[i] = 0,g[i].clear();
int f = 0;
for(int i = 1;i < n;++i)
{
int x,y;
scanf("%d %d",&x,&y);
deg[x] += 1;
deg[y] += 1;
g[x].push_back(node(y,i)),g[y].push_back(node(x,i));
all[i].id = i;
all[i].x = x,all[i].y = y;
if(deg[x] >= 3 || deg[y] >= 3) f = 1;
}
if(f)
{
puts("-1");
return ;
}
for(int i = 1;i <= n;++i)
{
if(deg[i] == 1)
{
for(int j = 1;j < n;++j)
{
if(all[j].x == i || all[j].y == i)
{
a[all[j].id] = 2;
dfs(i,0,2);
for(int j = 1;j < n;++j)
printf("%d%c",a[j]," \n"[j == n - 1]);
return ;
}
}
}
}
puts("-1");
}
int main()
{
// ini();
int t = 1;
scanf("%d",&t);
while(t--)
solve();
return 0;
}D
题意:
n个数,每一次操作你可以选择其中的两个数进行GCD,然后将得到的数字加入到序列的末尾,当然这个数字不能出现在原序列当中,问你最多操作几次。
分析:
①看到a的最值是1e6我们可以发现这里面一定有猫腻,那么我们可以每次对数字i进行判定,看看它能不能加入到我们的序列当中
②如果一个数能够加入进来,那么所有在序列中的数字能被这个数取余为0的,进行GCD操作一定会得到这个数,具体来说就是:
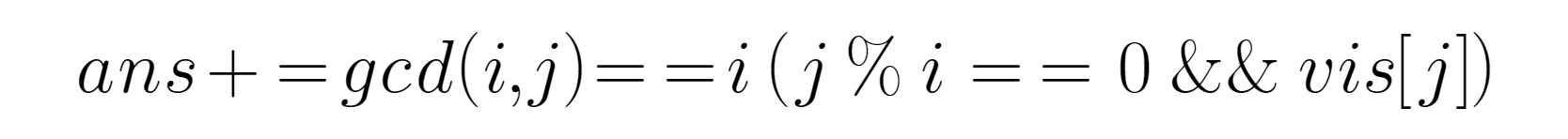
最终的答案就是ans - n
查看代码
#include <iostream>
#include <vector>
#include <cstring>
#include <map>
#include <algorithm>
using namespace std;
typedef long long ll;
const int MAXN = 1e6 + 7;
bool vis[MAXN];
bool prime[MAXN];
int p[MAXN],top = 0;
void ini()
{
for(int i = 2;i < MAXN;++i)
{
if(!prime[i]) p[++top] = i;
for(int j = 1;j <= top && 1ll * p[j] * i < MAXN;++j)
{
prime[p[j] * i] = 1;
if(i % p[j] == 0) break;
}
}
}
/*
2
4 16
*/
int gcd[MAXN];
void solve()
{
int n;
scanf("%d",&n);
for(int i = 1;i <= n;++i) {
int x;
scanf("%d",&x);
vis[x] = 1;
}
int ans = 0;
for(int i = 1;i <= 1e6;++i)
{
for(int j = i;j <= 1e6;j += i)
if(vis[j]) gcd[i] = __gcd(gcd[i],j);
ans += gcd[i] == i;
}
printf("%d\n",ans - n);
}
int main()
{
// ini();
int t = 1;
// scanf("%d",&t);
while(t--)
solve();
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号