二、 扩散模型（Diffusion Model）的训练过程

目录

• 1. 前向过程与反向过程
• 2. 扩散模型的训练过程
  • 训练过程第2步
  • 训练过程第3，4步
  • 训练过程第5步
  • 训练过程伪代码
• 3. 为什么可以从0时刻的图片\(\mathbf{x}_0\)直接生成t时刻的图片\(\mathbf{x}_t\)?
  • 从 \(\mathbf{x}_{t-1}\) 到 \(\mathbf{x}_t\)
  • 从 $\mathbf{x}_{0} $到 \(\mathbf{x}_t\)
  • 概率密度函数 \(q\left(\mathbf{x}_t \mid \mathbf{x}_{t-1}\right)\) 以及 \(q\left(\mathbf{x}_t \mid \mathbf{x}_0\right)\)

以下内容参考了Lil'Log 和李宏毅老师的课程

对于任何一个模型，都会分为两个过程：这篇文章主要聚焦于扩散模型的训练过程，而后面的文章将会聚焦于扩散模型的测试过程。

1. 前向过程与反向过程

训练过程中，我们需要向不含任何噪音的图片\(\mathbf{x}_0\)中加噪，是从到，再到的过程。这个过程称为前向过程，也叫做扩散过程。

测试过程中，我们需要从一个全是噪音的图片\(\mathbf{x}_T\)开始，逐渐降噪，最终生成想要的图片，是从到，再到的过程。这个过程称为反向过程，也叫做逆扩散过程。

为什么向图片中加噪叫做扩散过程？

想象一滴墨水倒在了水中，这滴墨水会在水中逐渐扩散，最终化在水中。

这个过程也可以理解为墨水从有序变得无序的过程。

同样的，如果我们有一张图片，那么我们可以向图片中添加噪音，使得图片从有序变得无序

就像墨水在水中扩散一样，因此叫做扩散过程。

2. 扩散模型的训练过程

训练过程的目的是：训练出一个可以预测噪音的模型Noise Predicter。训练结束后，使用Noise Predicter，可以生成我们想要的图片。

在论文中，扩散模型的训练过程如下

训练过程第2步

• 目的：

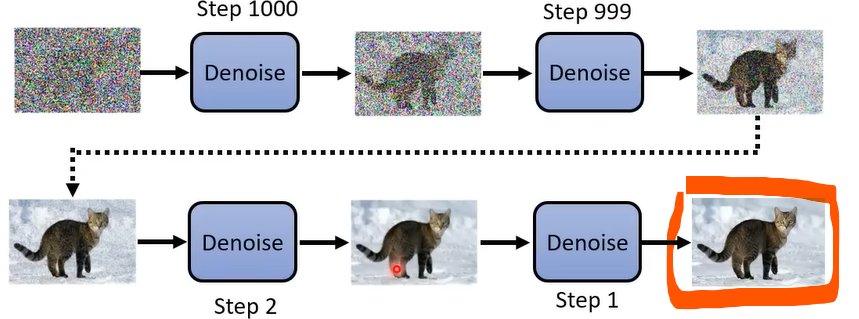
  生成一张不带任何噪音的图片\(\mathbf{x}_0\)。

  例如，下图中，红色框的图片就是不带任何噪音的图片。

  

• 公式讲解：

  \(q(\mathbf{x}_0)\)表示\(\mathbf{x}_0\)的满足的分布为\(q(\mathbf{x}_0)\)，因此\(\mathbf{x}_0\sim q(\mathbf{x}_0)\)表示从分布\(q(\mathbf{x}_0)\)中抽取一张图片\(\mathbf{x}_0\)。

若\(t\)时刻的图片为\(\mathbf{x}_t\)，那么\(\mathbf{x}_0\)是不带任何噪音的图片；\(\mathbf{x}_T\)是完全是噪音的图片，从\(\mathbf{x}_0\)到\(\mathbf{x}_T\)，图片中的噪音逐渐增加

训练过程第3，4步

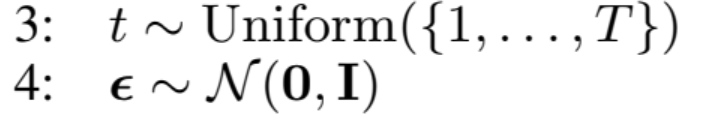
• 目的：

  从\([1,T]\)中随机抽取一个时刻\(t\)；并且从标准正态分布中，采样出噪音\(\boldsymbol {\epsilon}\)

• 公式讲解：

  \(t \sim \operatorname{Uniform}(\{1, \ldots, T\})\)表示从1到\(T\)的均匀分布中采样出一个\(t\)；\(\boldsymbol{\epsilon} \sim \mathcal{N}(\mathbf{0}, \mathbf{I})\)从标准正态分布中，采样出噪音\(\boldsymbol {\epsilon}\)。因为噪音\(\boldsymbol {\epsilon}\)是一个矩阵，所以在公式\(\boldsymbol{\epsilon} \sim \mathcal{N}(\mathbf{0}, \mathbf{I})\)中，\(\mathbf{0}\)表示零矩阵，\(\mathbf{I}\)表示单位矩阵。

训练过程第5步

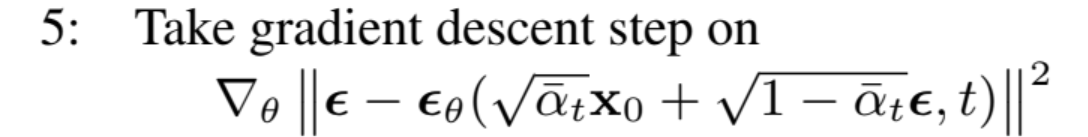
• 目的：

  计算损失函数关于参数\(\theta\)的梯度，从而更新参数参数\(\theta\)

• 公式讲解：

  • \(\sqrt{\bar{\alpha}_t} \mathbf{x}_0+\sqrt{1-\bar{\alpha}_t} \boldsymbol{\epsilon}\)表示\(t\)时刻的图片\(\mathbf{x}_t\)，其中\(\bar{\alpha_t}\)是一个常量。

    可以看到，这和我们上一篇文章中说的不太一样，对于\(\mathbf{x}_t\)的生成，不需要一步一步的从\(\mathbf{x}_0\)是生成\(\mathbf{x}_1\) ,从\(\mathbf{x}_1\)生成\(\mathbf{x}_2\) ...从\(\mathbf{x}_{t-1}\)生成\(\mathbf{x}_t\)，而是可以直接从\(\mathbf{x}_0\)生成\(\mathbf{x}_t\)。

    

  • \(\boldsymbol{\epsilon}_\theta\)就是上一篇文章说的Noise Predicter，即预测噪声的模型。

    它有两个输入：\(t\)时刻的图片\(\mathbf{x}_t\)（\(\mathbf{x_t} = \sqrt{\bar{\alpha}_t} \mathbf{x}_0+\sqrt{1-\bar{\alpha}_t} \boldsymbol{\epsilon}\)），以及时刻\(t\)。

    它的输出是：对噪音\(\boldsymbol{\epsilon }\)的预测值，记作\(\hat{\boldsymbol{\epsilon }}\)。

    Noise Predicter的输出也和上一篇文章不太一样。由于可以从\(\mathbf{x}_0\)直接生成\(\mathbf{x}_t\)，因此Noise Predicter的输出变成了从 0 时刻到 \(t\) 时刻，加入的噪音总和 \(\hat{\boldsymbol{\epsilon }}\) ；而不再是从 \(t-1\) 时刻到 \(t\) 时刻加入的噪音。

  • \(\left\|\boldsymbol{\epsilon}-\boldsymbol{\epsilon}_\theta\left(\sqrt{\bar{\alpha}_t} \mathbf{x}_0+\sqrt{1-\bar{\alpha}_t} \boldsymbol{\epsilon}, t\right)\right\|^2\)，也就是\(||\boldsymbol{\epsilon}-\hat{\boldsymbol{\epsilon}}||^2\)，表示模型的损失函数是均方误差损失，可以记作\(L_t\)。

  • \(\nabla_\theta\left\|\boldsymbol{\epsilon}-\boldsymbol{\epsilon}_\theta\left(\sqrt{\bar{\alpha}_t} \mathbf{x}_0+\sqrt{1-\bar{\alpha}_t} \boldsymbol{\epsilon}, t\right)\right\|^2\)，也就是\(\frac{\partial L_t}{\partial \theta}\)，表示损失函数\(L_t\)对参数\(\theta\)的梯度。

训练过程伪代码

训练过程的伪代码如下：

while True:
	# 第2步
	挑出一张没有噪音的图片x_0
    
	# 第3步
	在[1,T]中，随机选出一个时刻t
    
	# 第4步
	生成一个噪音ε
    
	# 第5步
    生成t时刻的图片x_t
	y_pred = ε_θ(x_t,t) # 预测噪音的模型是ε_θ，y_pred为ε_θ输出的预测值
	y = ε # 真实值是噪音ε
	loss = (y-y_pred)**2
	计算loss关于参数θ的损失
	更新参数θ
    
    # 第6步
    if 模型ε_θ 已经收敛: 
        break

3. 为什么可以从0时刻的图片\(\mathbf{x}_0\)直接生成t时刻的图片\(\mathbf{x}_t\)?

从 \(\mathbf{x}_{t-1}\) 到 \(\mathbf{x}_t\)

设\(t\)时刻的图片为\(\mathbf{x}_t\)，\(t-1\)时刻的图片为\(\mathbf{x}_{t-1}\)，\(t-1\)时刻向\(t\)时刻加入的噪音为\(\boldsymbol{\epsilon}_{t}\)，并且假设\(\boldsymbol{\epsilon}_{t}\sim N(0,1)\)，扩散模型规定，将噪音\(\boldsymbol{\epsilon}_{t}\)加入到图像\(\mathbf{x}_{t-1}\)中的公式为：

\[\mathbf{x}_t = \sqrt{1-\beta_t} \times {\mathbf{x}_{t-1}}+\sqrt{\beta_t} \times \boldsymbol{\epsilon}_{t-1} \tag{1} \]

其中\(\beta_t\)是一个常数，并且从\(t=0\)到\(t=T\)，\(\beta_t\)的值逐渐增大。这代表着，从\(t=0\)到\(t=T\)，向图片中增加的噪音越来越多。

若一开始的清晰的图片为\(\mathbf{x}_0\)，根据公式（1），我们就可以逐步加噪，最终生成充满噪音的图片\(\mathbf{x}_T\)。

从 $\mathbf{x}_{0} $到 \(\mathbf{x}_t\)

考虑这样一个问题，如果逐步迭代：根据\(\mathbf{x}_0\)计算\(\mathbf{x}_1\)，根据\(\mathbf{x}_1\)计算\(\mathbf{x}_2\)，...，这样的速度也太慢了。

所以，我们可以考虑简化一下公式，最好是能够推导出直接从\(\mathbf{x}_0\)生成\(\mathbf{x}_T\)的公式。

我们将常数\(\beta_t\)换一种表达方式，令\(\alpha_t = 1-\beta_t\)，那么根据公式（1），我们可以得到

\[\begin{align} \mathbf{x}_t&=\sqrt{\alpha_t} \times \mathbf{x}_{t-1} + \sqrt{1-\alpha_t} \times \boldsymbol{\epsilon_t} \tag{2}\\ \mathbf{x}_{t-1}&=\sqrt{\alpha_{t-1}} \times \mathbf{x}_{t-2} + \sqrt{1-\alpha_{t-1}} \times \boldsymbol{\epsilon_{t-1}} \tag{3} \end{align} \]

将公式（3）带入到公式（2）中，可以得到

\[\begin{aligned} \mathbf{x}_t&=\sqrt{\alpha_t} \times\left(\sqrt{\alpha_{t-1}} \times \mathbf{x}_{t-2} + \sqrt{1-\alpha_{t-1}} \times \boldsymbol{\epsilon_{t-1}} \right)+\sqrt{1-\alpha_t} \times \boldsymbol\epsilon_t\\ &=\sqrt{\alpha_t \alpha_{t-1}} \times \mathbf{x}_{t-2}+\sqrt{\alpha_t\left(1-\alpha_{t-1}\right)} \boldsymbol{\epsilon}_{t-1}+\sqrt{1-\alpha_t} \times \boldsymbol{\epsilon}_t \end{aligned} \]

因为\(\boldsymbol{\epsilon}_{t}\sim N(0,1)\)，\(\boldsymbol{\epsilon}_{t-1}\sim N(0,1)\)，因此，\(\left[\sqrt{\alpha_t\left(1-\alpha_{t-1}\right)} \boldsymbol{\epsilon}_{t-1}+\sqrt{1-a_t} \times \boldsymbol{\epsilon}_t\right]\sim N\left(0,1-\alpha_t \alpha_{t-1}\right)\)

如果我们另设一个噪音\(\boldsymbol{\epsilon}\sim N(0,1)\)，那么\(\sqrt{1-\alpha_t \alpha_{t-1}} \boldsymbol{\epsilon}\sim N(0,1-\alpha_t \alpha_{t-1})\)

因此，我们可以令\(\left[\sqrt{\alpha_t\left(1-\alpha_{t-1}\right)} \boldsymbol{\epsilon}_{t-1}+\sqrt{1-a_t} \times \boldsymbol{\epsilon}_t\right] = \sqrt{1-\alpha_t \alpha_{t-1}} \boldsymbol{\epsilon}\)​

上面这种改写方式被称为“重参数化技巧”。

于是可以得到从\(\mathbf{x}_{t-2}\)得到\(\mathbf{x}_t\)的公式

\[\mathbf{x}_t=\sqrt{\alpha_t \alpha_{t-1}} \times \mathbf{x}_{t-2}+\sqrt{1-\alpha_t \alpha_{t-1}} \boldsymbol{\epsilon} \]

不断重复上面的过程，最终我们可以得到从\(\mathbf{x}_0\)到\(\mathbf{x}_t\)的公式

\[\mathbf{x}_t=\sqrt{\bar{\alpha}_t} \times \mathbf{x}_0 +\sqrt{1-\bar{\alpha}_t} \times \boldsymbol\epsilon\tag{4} \]

其中，\(\bar{\alpha}_t=\alpha_t \alpha_{t-1} \alpha_{t-2} \alpha_{t-3} \ldots \alpha_2 \alpha_1 = \prod_{i=1}^{t}\alpha_i\)，\(\boldsymbol\epsilon\sim N(0,1)\)。

至此，我们得到前向过程的公式，即公式（4）

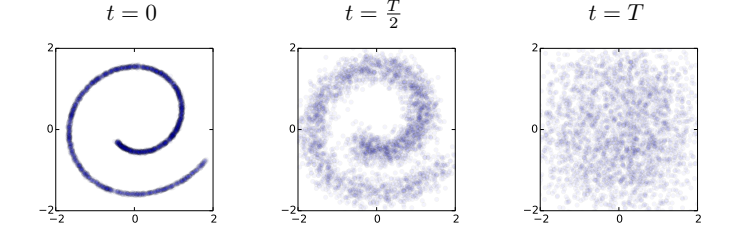
我们前面说过，\(\beta_1<\beta_2<\cdots<\beta_T\),因此\(\bar{\alpha}_1>\cdots>\bar{\alpha}_T\)。当\(t=T\)时，\(\bar{\alpha}_T \approx 0\)，\(\mathbf{x}_T \approx \boldsymbol\epsilon\)，即\(\mathbf{x}_T\)可以近似认为服从标准正态分布。

概率密度函数 \(q\left(\mathbf{x}_t \mid \mathbf{x}_{t-1}\right)\) 以及 \(q\left(\mathbf{x}_t \mid \mathbf{x}_0\right)\)

根据公式（1），我们可以得到，在前向过程中，在已知\(\mathbf{x}_{t-1}\)的条件下，\(\mathbf{x}_t\)的概率密度函数\(q\left(\mathbf{x}_t \mid \mathbf{x}_{t-1}\right)=\mathcal{N}\left(\mathbf{x}_t ; \sqrt{1-\beta_t} \mathbf{x}_{t-1}, \beta_t \mathbf{I}\right)\)

根据公式（4），我们可以得到，在前向过程中，在已知\(\mathbf{x}_{0}\)的条件下，\(\mathbf{x}_t\)的概率密度函数\(q\left(\mathbf{x}_t \mid \mathbf{x}_0\right)=\mathcal{N}\left(\mathbf{x}_t ; \sqrt{\bar{\alpha}_t} \mathbf{x}_0,\left(1-\bar{\alpha}_t\right) \mathbf{I}\right)\)

\(\mathcal{N}\left(\mathbf{x}_t ; \sqrt{\bar{\alpha}_t} \mathbf{x}_0,\left(1-\bar{\alpha}_t\right) \mathbf{I}\right)\)表示随机变量为\(\mathbf{x}_t\)，均值为\(\sqrt{\bar{\alpha}_t} \mathbf{x}_0\)，方差为\(\left(1-\bar{\alpha}_t\right) \mathbf{I}\)的正态分布。