CodeForces 908C. New Year and Curling 解题报告 Java

1. 思路

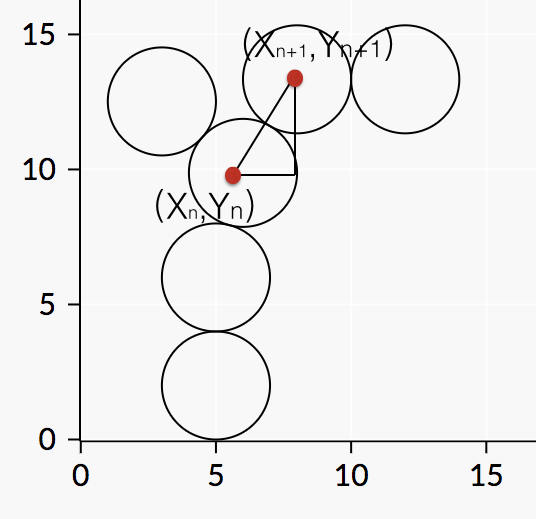
这题实际上是个几何问题——两个外相切的圆，由勾股定理，他们的纵坐标有以下的规律：

则有$$y_{n+1} = y_{n} + \sqrt{(2r)^2 - (x_{n} - x_{n+1})^2}$$

其中x代表横坐标，y代表纵坐标，r代表半径。 简略画了个图：

 

2. 容易错的地方

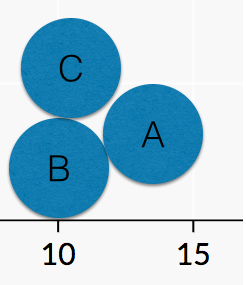
非常直观的想法是，“设有两个圆A、B都在与C相切的直径范围内，那么如果y[A] > y[B], 则 y[A]+ ΔyA > y[B] + ΔyB，所以y[A]+ ΔyA就是C的纵坐标”.但是这是错的，我画了个图：

 

3.代码

   public static void main(String[] args) {
       Scanner in = new Scanner(System.in);
       int n = in.nextInt();
       double r = in.nextDouble();
       int[] x = new int[n];
       double[] y = new double[n];
       for(int i = 0; i < n; ++i) 
           x[i] = in.nextInt();
       for(int i = 0; i < n; ++i) {
           y[i] = r;
           for(int j = 0; j < i; ++j) {
               if(Math.abs(x[i] - x[j]) <= 2*r)
                {
                    double delta = Math.sqrt(4*r*r - (x[i]-x[j])*(x[i]-x[j]));
                    if(delta + y[j] > y[i])
                        y[i] = delta + y[j];
                }
           }
           System.out.print(i==0 ? y[i] : " " + y[i]);
       }       
   }