刷题笔记Day23回溯算法part02
刷题笔记Day23:回溯算法part02
题目:组合总和
给你一个 无重复元素 的整数数组 candidates 和一个目标整数 target ,找出 candidates 中可以使数字和为目标数 target 的 所有 不同组合 ,并以列表形式返回。你可以按 任意顺序 返回这些组合。
candidates 中的 同一个 数字可以 无限制重复被选取 。如果至少一个数字的被选数量不同,则两种组合是不同的。
对于给定的输入,保证和为 target 的不同组合数少于 150 个。
示例 1:
输入:candidates = [2,3,6,7], target = 7
输出:[[2,2,3],[7]]
解释:
2 和 3 可以形成一组候选,2 + 2 + 3 = 7 。注意 2 可以使用多次。
7 也是一个候选, 7 = 7 。
仅有这两种组合。
反思:在写本体的时候我还是按照Day22中的思路去写,发现一个问题就是无法实现代码中的去重逻辑,如果按照之前的逻辑写,每一次for循环都去遍历一遍整个candidates,这样写随让能找到所有的元素但是回碰到找到的元素包含[2,2,3],[2,3,2],[3,2,2]这三种情况,因此为了避免在这种现象的发生,需要进行去重操作,在此处使用的是入下图中的逻辑,在向前递归的过程中增加开始变量让for循环的起始位置在第一次进入递归的位置之后,如下图一样,当从3开始递归时候他在向下递归的过程中只能选择[3,6,7]这几个数字。
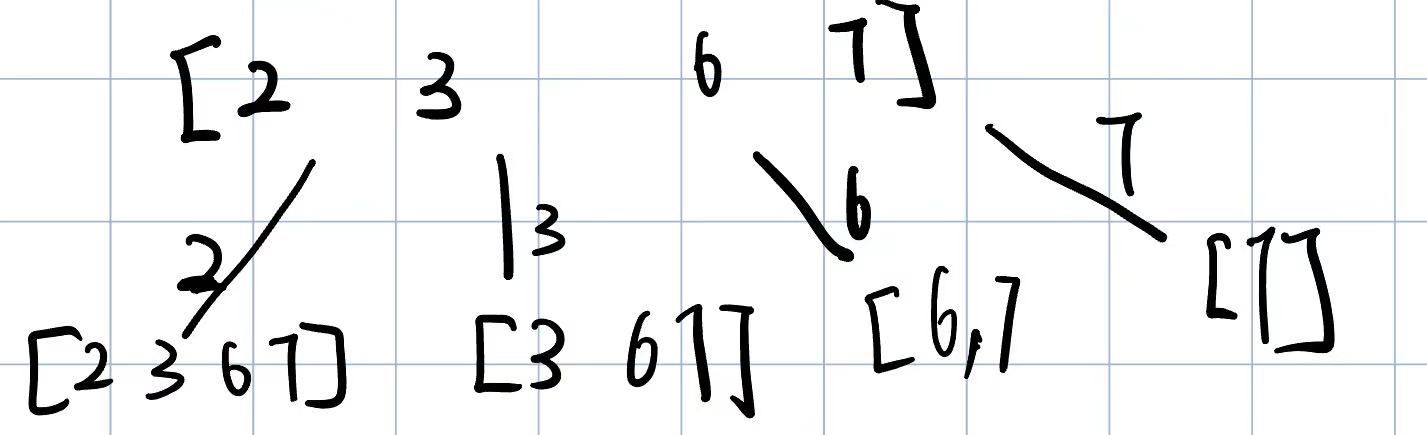
代码:
class Solution {
public:
vector<int> nums;
vector<vector<int>> result;
void backtracking(vector<int>& candidates, int index, int target)
{
//终止条件
int nums_sum = 0;
for(int i = 0; i <nums.size();i++)
{
nums_sum += nums[i];
}
if(nums_sum >= target )
{
if(nums_sum == target)
{
result.push_back(nums);
}
return;
}
//for循环处理横向逻辑
for(int i = index;i<candidates.size();i++)
{
nums.push_back(candidates[i]);
backtracking(candidates,i,target);
nums.pop_back();
}
return;
}
vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
backtracking(candidates,0,target);
return result;
}
};
题目:组合总和 II
给定一个候选人编号的集合 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。
candidates 中的每个数字在每个组合中只能使用 一次 。
注意:解集不能包含重复的组合。
示例 1:
输入: candidates = [10,1,2,7,6,1,5], target = 8,
输出:
[
[1,1,6],
[1,2,5],
[1,7],
[2,6]
]
思路:本体的代码核心和上体一样是去重逻辑,本体要求candidates 中的每个数字在每个组合中只能使用 一次 ,因此像[1,1,6],[1,6,1],[6,1,1]是有问题的。为了实现去重逻辑需要对candidates进行排序,排序后的candidates=[1,1,2,5,6,7,10],为了实现递归横向的逻辑及for循环中的去重逻辑可以看代码中的i>index && candidates[i] == candidates[i-1],首先要确保不是递归后子集的首数字,其次若是前一个数字和当前数字相同说明当前这一个数字就不用进行递,因为在上一个值的递归的过程中已经将这个数字的所有可能都包含了。其逻辑如下图,跳过处即为去重逻辑,第二个1的所有组合可能都被第一个1所包含了。

class Solution {
public:
vector<int> nums;
vector<vector<int>> result;
void backtracking(vector<int>& candidates, int index, int target)
{
//终止条件
int nums_sum = 0;
for(int i = 0; i <nums.size();i++)
{
nums_sum += nums[i];
}
if(nums_sum >= target || nums.size() == candidates.size())
{
if(nums_sum == target)
{
result.push_back(nums);
}
return;
}
//for循环处理横向逻辑
for(int i = index;i<candidates.size();i++)
{
if(i>index && candidates[i] == candidates[i-1])
{
continue;
}
nums.push_back(candidates[i]);
backtracking(candidates,i+1,target);
nums.pop_back();
}
return;
}
vector<vector<int>> combinationSum2(vector<int>& candidates, int target) {
sort(candidates.begin(),candidates.end());
backtracking(candidates,0,target);
return result;
}
};
题目:分割回文串
给你一个字符串 s,请你将 s 分割成一些 子串,使每个子串都是 回文串 。返回 s 所有可能的分割方案。
示例 1:
输入:s = "aab"
输出:[["a","a","b"],["aa","b"]]
示例 2:
输入:s = "a"
输出:[["a"]]
思路:通过递归的方式遍历所有可能子串,在遍历的过程中子串的过程中筛选是否为回文串,遍历的逻辑如下:

代码:(一定要注意切割子串的起始位置和终止位置)
class Solution {
public:
vector<string> one;
vector<vector<string>> result;
void backtracking(string s , int start_index)
{
//判断在递归之前,因此此处仅作为结果的收集
if(start_index == s.size())
{
result.push_back(one);
return;
}
for(int i = start_index;i<= s.size();i++)
{
//切割子串(记住这个start_index,这是起始切割位置,第一遍没做出来就是卡在这里)
string tmp(s.begin()+start_index,s.begin()+i+1);
//翻转子串
string tmp_reverse(tmp.rbegin(),tmp.rend());
//若是回文子串则进入递归
if(tmp == tmp_reverse)
{
one.push_back(tmp);
backtracking(s, i+ 1);
one.pop_back();
}
}
}
vector<vector<string>> partition(string s) {
backtracking(s,0);
return result;
}
};


 浙公网安备 33010602011771号
浙公网安备 33010602011771号