刷题笔记Day22回溯算法part01
刷题笔记Day22:回溯算法part01
回溯算法在之前递归中就有涉及,例如之前的所有可能路径的题目就用到了回溯的思想
回溯出现的位置都是在递归之后,且回溯就是纯的暴力算法。(解决for循环无法暴力破解的方法)
回溯所要解决的问题
- 组合问题
- 切割问题
- 子集问题
- 排列问题
- 棋盘问题
回溯问题都可以看成是一个N叉树的问题,下面引用一张代码随想录中的图片便于理解
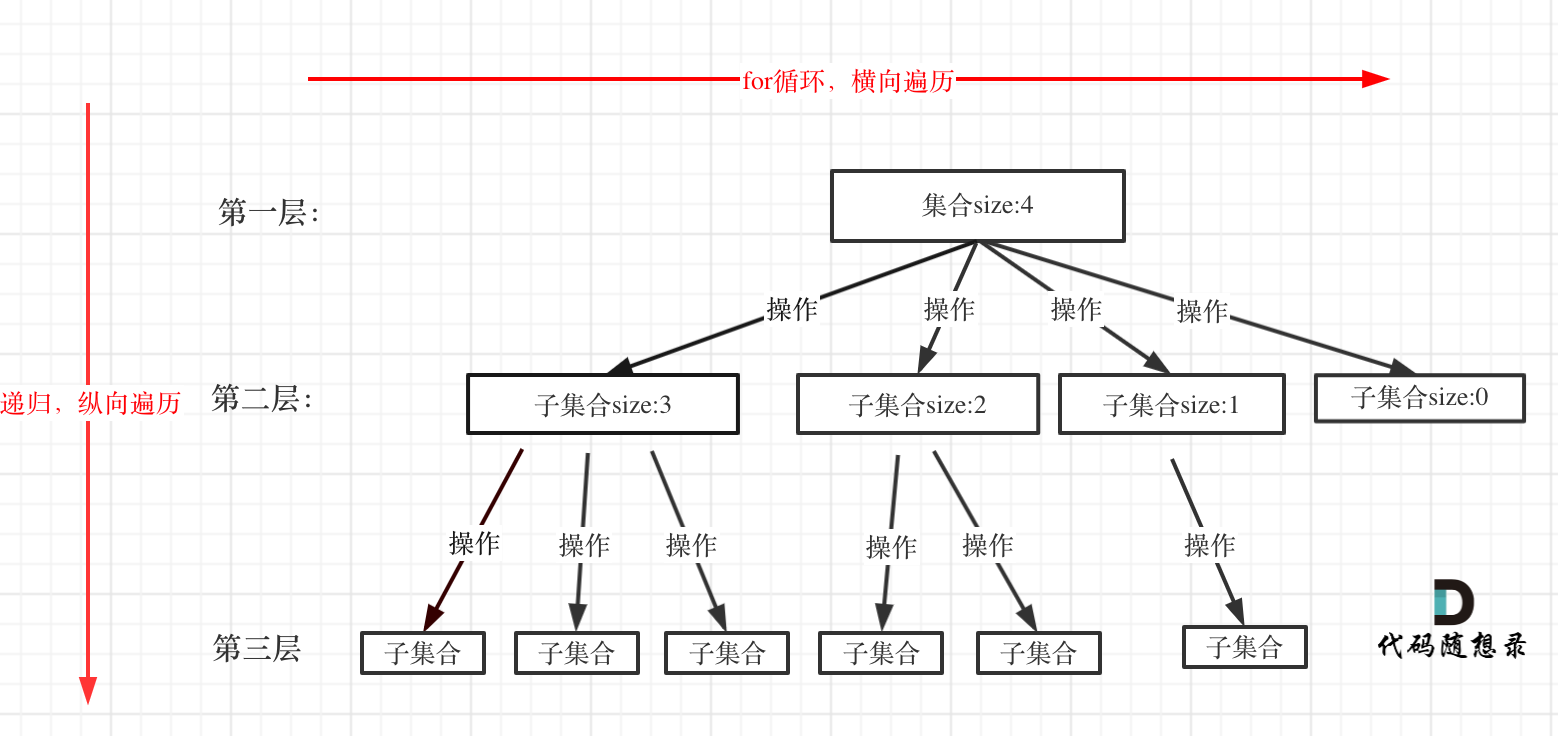
回溯算法模板框架:
void backtracking(参数) {
if (终止条件) {
存放结果;
return;
}
for (选择:本层集合中元素(树中节点孩子的数量就是集合的大小)) {
处理节点;
backtracking(路径,选择列表); // 递归
回溯,撤销处理结果
}
}
题目:77. 组合
组合
给定两个整数 n 和 k,返回范围 [1, n] 中所有可能的 k 个数的组合。
你可以按 任何顺序 返回答案。
思路:可以将整个过程转化为N叉树的模式,横向即为for循环为纵向即为递归逻辑,而终止条件即为我们需要多少层的for循环,在本题中为k个for循环。

代码:如下:
class Solution {
public:
vector<vector<int>> result;
vector<int>tmp;
void backtracking(int start, int end,int k){
if(k == 0){
result.push_back(tmp);
return;
}
for(int i = start;i<= end-k+1;i++)
{
tmp.push_back(i);
backtracking(i+1,end,k-1);
tmp.pop_back();
}
}
vector<vector<int>> combine(int n, int k) {
backtracking(1,n,k);
return result;
}
};
题目:组合总和 III
思路:和上一题相同想办法将其转化为N叉树,代码如下
class Solution {
public:
vector<vector<int>>result;
vector<int> tmp;
void backtracking(int start,int k, int n)
{
if(k == 0)
{
int tmp_sum = 0;
for(int k = 0; k< tmp.size();k++)
{
tmp_sum += tmp[k];
}
if(tmp_sum == n)
{
result.push_back(tmp);
}
return;
}
for(int i = start; i<= 9-k+1;i++)
{
tmp.push_back(i);
int tmp_sum = 0;
//减枝
for(int z = 0; z< tmp.size();z++)
{
tmp_sum += tmp[z];
}
if(tmp_sum > n)
{
tmp.pop_back();
break;
}
backtracking(i+1,k-1,n);
tmp.pop_back();
}
return;
}
vector<vector<int>> combinationSum3(int k, int n) {
backtracking(1,k,n);
return result;
}
};
题目:17. 电话号码的字母组合
17. 电话号码的字母组合
思路:本体的思路和上面略有不同,上面两题的集合都是在同一个集合中取值,而本体的集合是单独的一个个集合,因此每层for循环的逻辑回变得即为的清晰,相较于上面两题而言较为容易,此题直接给出代码
class Solution {
private:
const string letterMap[10] = {
"", // 0
"", // 1
"abc", // 2
"def", // 3
"ghi", // 4
"jkl", // 5
"mno", // 6
"pqrs", // 7
"tuv", // 8
"wxyz", // 9
};
public:
string tmp;
vector<string> result;
void backtracking(const string& digits, int index)
{
if(index == digits.size())
{
result.push_back(tmp);
return;
}
int index_map = digits[index] - '0';
string s = letterMap[index_map];
for(int i = 0; i< s.size();i++)
{
tmp.push_back(s[i]);
backtracking(digits,index+1);
tmp.pop_back();
}
}
vector<string> letterCombinations(string digits) {
tmp.clear();
result.clear();
if(digits.size() == 0){
return result;
}
backtracking(digits,0);
return result;
}
};


 浙公网安备 33010602011771号
浙公网安备 33010602011771号