一元三次方程学习报告
定义
如果一个整式方程经过整理后只有一个未知数,并且未知数的最高次项等于 \(3\),这样的方程称作一元三次方程。
一元三次方程是形如 \(ax^3+bx^2+cx+d=0(a \ne 0)\) 的方程,其中 \(a,b,c,d\) 分别称作三次项系数,二次项系数,一次项系数和常数项。同样地,我们称函数 \(y=ax^3+bx^2+cx+d(a \ne 0)\) 为三次函数。
例 1:观察下列方程,它们是一元三次方程吗?
- \(x^3+\frac{1}{x^2}+\frac{1}{x}-2=0\);
- \(ax^3+bx+c=0\);
- \(\sqrt{a^2+1}x^3+bx^2-cx=0\);
- \((x+1)^4=x^2(x^2+4x)\);
- \(2(x+1)^2=3(x+1)^3\)。
解析:3. 5. 是,1. 2. 4. 不是。因为 1. 不满足整式方程;2. 没有说 \(a \ne 0\);3. 因为 \(\sqrt{a^2+1} \ge 1\),所以隐含了三次项系数不为 \(0\) 的条件;4. 化简后是 \(6x^2+4x+1=0\),最高次项为 \(2\);5. 化简后是 \(3x^3+7x^2+5x+1=0\),是一元三次方程。
求解一元三次方程
研究一个代数问题,可以按照从特殊到一般的方法层层递进。
配立方法
对于一元二次方程,我们可以把它配成 \((x+h)^2=\frac{k}{a}\) 的形式,如果我们可以把一元三次方程配成 \((x+h)^3=\frac{k}{a}\) 的形式,那么问题也就迎刃而解了。
但是所有的一元三次方程都可以使用配立方法吗?
例2:尝试使用配立方法解如下方程:
- \(x^3+6x^2+12x+9=0\);
- \(x^3+3x+1=0\)。
解析:
对于第一个:
\[\begin{aligned} x^3+6x^2+12x+9 &= 0 \\ x^3+3\cdot x^2 \cdot 2+3 \cdot x \cdot 2^2 +8 &= -1 \\ (x+2)^3 &= -1 \\ x &= -3 \end{aligned}\]但是对于第二个方程,无论如何都无法使用配立方法求解。
考虑什么样的方程可以使用配立方法求解?
尝试展开 \((x+h)^3=\frac{k}{a}\),可得 \(ax^3+3ahx^2+3ah^2x+ah^3-k=0\),与方程 \(ax^3+bx^2+cx+d=0\) 做比较,可得
因而得到数量关系 \(b^2-3ac=0\)。因此,只要 \(b^2-3ac=0\),那么这个方程就可以直接使用配立方法求解。
例3:判断如下的方程是否可以直接使用配立方法求解。
- \(x^3-6x^2+11x-6=0\);
- \(8x^3-12x^2+6x-7=0\);
- \(2\sqrt 2x^3+4 \sqrt 3x^2 +4 \sqrt 2x-8=0\)。
解析:分别计算三个方程的 \(b^2-3ac\) 即可。
对于第一个方程,\(b^2-3ac=36-33 \ne 0\),所以不行;
对于第二个方程,\(b^2-3ac=144-144 = 0\),所以可以;
对于第一个方程,\(b^2-3ac=48-48 = 0\),所以可以。
因式分解法
如果我们能够很容易地看出来方程的一个根,那么可以考虑把这个一元三次方程“降次”,变成一元二次方程然后求解。
例4: 在实数范围内解下列方程。
- \(4x^3+9x^2-x-6=0\);
- \(x^3+6x^2+5x-12=0\);
- \(3x^3+2x^2-32=0\)。
解析:
对于第一个方程,代入 \(x=-1\),可得左式 \(=-4+9+x-6=0\),所以 \(x=-1\) 是原方程的一个根,所以原方程必然有一个因式为 \(x+1\)。考虑凑出 \(x+1\),可得 \(4x^3+4x^2+5x^2+5x-6x-6=0\),即 \(4x^2(x+1)+5x(x+1)-6(x+1)=0\),提出公因式 \(x+1\),可得 \((4x^2+5x-6)(x+1)=0\),最终可以因式分解成 \((4x-3)(x+2)(x+1)=0\)。
所以原方程的三个实数根分别为 \(x_1=\frac{3}{4},x_2=-2,x_3=-1\)。
对于第二个方程,可以看出 \(x=1\) 是原方程的根,所以原方程可以因式分解成 \((x^2+7x+12)(x-1)=0\),进而因式分解成 \((x+3)(x+4)(x-1)=0\)。
所以原方程的三个实数根分别为 \(x_1=-4,x_2=-3,x_3=1\)。
对于第三个方程,可以试出 \(x=2\) 是原方程的根,所以原方程可以因式分解成 \((3x^2+8x+16)(x-2)=0\)。该式子不能继续因式分解了。
所以原方程的唯一实数根为 \(x=2\)。
卡尔丹诺公式
先考虑一种特殊形式的三次方程:\(x^3+px+q=0\)。这样的方程缺少二次项。
接下来就是处理这个方程比较神奇的地方:令 \(x=u+v\)。(假设 \(u>v\))
代入可得 \((u+v)^3+p(u+v)+q=0\)。
整理可得 \(u^3+v^3+(3uv+p)(u+v)+q=0\)。
因为 \(u\) 和 \(v\) 到现在只需满足 \(x=u+v\) 这个限制,不妨让它再多满足一个限制 \(3uv+p=0\)。
如果这样可行,我们可以得到这样的方程:\(\begin{cases}u^3+v^3=-q \\ uv=-\frac{p}{3}\end{cases}\)。
第二个式子等式两边同时三次方,可得 \(u^3v^3=-\frac{p^3}{27}\)。
因此可以解得 \(u^3=-\frac{q}{2}+\sqrt{\frac{q^2}{4}+\frac{p^3}{27}},v^3=-\frac{q}{2}-\sqrt{\frac{q^2}{4}+\frac{p^3}{27}}\)。
所以 \(x=u+v=\sqrt[3]{-\frac{q}{2}+\sqrt{\frac{q^2}{4}+\frac{p^3}{27}}}+\sqrt[3]{-\frac{q}{2}-\sqrt{\frac{q^2}{4}+\frac{p^3}{27}}}\)。
一般三次方程的转化
对于一般的一元三次方程 \(ax^3+bx^2+cx+d=0 (a \ne 0)\),都可以转化成以上形式的方程。
考虑令 \(x=y+m\),确定 \(m\) 的取值,可以消去二次项。我们先代入 \(x=y+m\):
\[\begin{aligned} & ax^3+bx^2+cx+d \\= & a(y+m)^3+b(y+m)^2+c(y+m)+d \\= & ay^3+(3am+b)y^2+(3am^2+2bm+c)y+(am^3+bm^2+cm+d) \end{aligned}\]
所以令 \(3am+b=0\),即 \(m=-\frac{b}{3a}\) 是可以令二次项系数化为 \(0\) 的 \(m\)。
例5:运用以上方法解方程 \(x^3-3x^2-9x+27=0\)。
首先把它转化成缺项形式,令 \(m=-\frac{b}{3a}=1\),代入 \(x=y+1\) 可得
\((y+1)^3-3(y+1)^2-9(y+1)+27=0\),化简可得 \(y^3-12y+16=0\)。
所以 \(p=-12,q=16\),代入以上公式,可得
\(u=\sqrt[3]{-\frac{16}{2}+\sqrt{\frac{16^2}{4}+\frac{(-12)^3}{27}}}=-2,v=\sqrt[3]{-\frac{16}{2}-\sqrt{\frac{16^2}{4}+\frac{(-12)^3}{27}}}=-2\)。
所以原方程的一个根为 \(y=u+v=-4\),此时 \(x=y+1=-3\)。
将原方程进行降次,可得 \((x+3)(x^2-6x+9)=0\),即 \((x+3)(x-3)^2=0\),所以原方程有两个根 \(x_1=3,x_2=-3\)。
注意以上的公式不能求出一个一元三次方程的所有根,在求出一个根之后,还需要进行降次得到另外的根。
复数的引入
请尝试解方程 \(x^3-15x-4=0\)。
如果还是使用以上的方法解方程,你会发现这个方程的根是“无意义的”:
但是,对于原方程,容易发现代入 \(x=4\) 是满足条件的。
那么是哪里出问题了呢?
假设我们令 \(i=\sqrt{-1}\),并定义 \(i^2=-1\),那么我们可以进行如下的变形:
神奇!把它展开以后,\(i\) 居然消掉了,并且得出了正确的结果。
这启示我们,可能 \(\sqrt{-1}\) 不是一种无意义的运算,如果能够在解三次方程的时候假设它是 “有意义” 的,也是没有关系的,因为它能够得出正确的结果。
复数范围内的解
卡尔达诺公式不能求出一个缺项的一元三次方程的所有解,那么是否有可能把这个公式“升级”,使得它能够求出所有解呢?
在复数范围内,对一个数 \(a\) 开根,相当于在复数域解方程 \(x^3-a=0\)。
首先在实数域中可以因式分解:\((x-\sqrt[3]{a})(x^2+\sqrt[3]{a}x+{a}^{\frac{2}{3}})=0\)。
然后使用求根公式,\(x^2+\sqrt[3]{a}x+{a}^{\frac{2}{3}}=0\) 的两根为
所以在复数域中,令 \(\omega=\frac{-1+\sqrt{3}i}{2}\),那么 \(x^3-a=0\) 的根为 \(x_1=\sqrt[3]{a},x_2=\omega \sqrt[3]{a},x_3=\omega^2 \sqrt[3]{a}\)。
我们再回顾一下卡尔达诺公式的推导过程,我们实际上是在解方程 \(\begin{cases}u^3+v^3=-q \\ uv=-\frac{p}{3}\end{cases}\),然后第二个式子同时 \(3\) 次方,得到了 \(\begin{cases}u^3+v^3=-q \\ u^3v^3=-\frac{p^3}{27}\end{cases}\),然后得到了
因此得到了 \(u^3=-\frac{q}{2}+\sqrt{\frac{q^2}{4}+\frac{p^3}{27}},v^3=-\frac{q}{2}-\sqrt{\frac{q^2}{4}+\frac{p^3}{27}}\)。
根据以上的推导过程,设 \(u_1=\sqrt[3]{-\frac{q}{2}+\sqrt{\frac{q^2}{4}+\frac{p^3}{27}}},u_2=\omega \sqrt[3]{-\frac{q}{2}+\sqrt{\frac{q^2}{4}+\frac{p^3}{27}}},u_3=\omega^2 \sqrt[3]{-\frac{q}{2}+\sqrt{\frac{q^2}{4}+\frac{p^3}{27}}}\),\(v\) 同理,这些 \(u,v\) 都是满足以上条件的数,那么这个一元三次方程有 \(9\) 个根?这显然不正确。
原来在同时三次方的过程中,会导致最终出现增根。例如 \(u_1,v_2\) 它满足 \(u^3v^3=-\frac{p^3}{27}\),但是不满足 \(uv=-\frac{p}{3}\)。
舍去增根以后,就只有三个根满足条件了。
这样我们就得到了一元三次方程的通解了。
盛金公式
用以上的方法解一元三次方程是非常麻烦的。首先我们需要进行代数变形去除掉二次项,然后代入以上的公式。代入以上的公式会导致解的形式可能出现复数,不是很直观,需要进行化简才能得到最终结果。这样对计算机很不友好。如果三次方程的系数比较奇怪,运用以上的公式以后可能都不知道从何化简。
有没有一些更直观的公式呢?接下来我们介绍盛金公式。
对于一般的一元三次方程 \(ax^3+bx^2+cx+d=0(a \ne 0)\),规定 \(\begin{cases} A=b^2-3ac \\ B=bc-9ad \\ C=c^2-3bd \end{cases}\),判别式 \(\Delta=B^2-4AC\)。
当 \(A=B=0\) 时,方程有三个相等的实根,\(x_1=x_2=x_3=-\frac{b}{3a}=-\frac{c}{b}=-\frac{3d}{c}\)。(盛金公式 \(1\))
当 \(\Delta>0\) 时,方程有一个实根,\(x_1=\frac{-b-(\sqrt[3]{y_1}+\sqrt[3]{y_2})}{3a}\),其中 \(y_{1,2}=Ab+3a(\frac{-B \pm \sqrt{B^2-4AC}}{2})\)。(盛金公式 \(2\))
当 \(\Delta=0\) 时,方程有三个实根,\(x_1=-\frac{b}{a}+K,x_2=x_3=-\frac{K}{2}\),其中 \(K=\frac{B}{A}\)。(盛金公式 \(3\))
当 \(\Delta<0\) 时,方程有三个实根,\(x_1=\frac{-b-2\sqrt{A}\cos{\frac{\theta}{3}}}{3a},x_{2,3}=\frac{-b+\sqrt{A}(\cos{\frac{\theta}{3}}\pm\sqrt 3\sin{\frac{\theta}{3}})}{3a}\),其中 \(\theta=\arccos \frac{2Ab-3aB}{2 \sqrt{A^3}}\)。(盛金公式 \(4\))
例6:解以下方程。
- \(x^3+3x+1=0\);
- \(5\sqrt 2 x^3-18x^2+6\sqrt 2x+4=0\)。
解析:
对于第一个方程:\(a=1,b=0,c=3,d=1\),计算得 \(A=-9,B=-9,C=9\),计算 \(\Delta=405>0\),运用盛金公式 \(2\)。
计算 \(y_{1,2}=\frac{3}{2}(9\pm 9\sqrt{5})\),所以 \(x=\frac{-\sqrt[3]{\frac{3}{2}(9+ 9\sqrt{5})}-\sqrt[3]{\frac{3}{2}(9- 9\sqrt{5})}}{3}\)。对于第二个方程:\(a=5\sqrt 2,b=-18,c=6\sqrt 2,d=4\),计算得 \(A=144,B=-288\sqrt 2,C=288\),计算 \(\Delta=0\),运用盛金公式 \(3\)。
计算 \(K=\frac{B}{A}=-2\sqrt 2\),所以 \(x_1=\frac{18}{5\sqrt 2}-2\sqrt 2=-\frac{\sqrt 2}{5}\),\(x_2=x_3=-\frac{-2\sqrt 2}{2}=\sqrt 2\)。
三次方程韦达定理
用求根公式推韦达定理固然可行,但是我们可以用一种更简单的方法。
设一元三次方程 \(ax^3+bx^2+cx+d\) 的三根分别是 \(x_1,x_2,x_3\),那么原方程可以分解成 \(a(x-x_1)(x-x_2)(x-x_3)=0\)。展开可得 \(ax^3-a(x_1+x_2+x_3)x^2+a(x_1x_2+x_2x_3+x_3x_1)x-ax_1x_2x_3=0\)。
对比系数可知 \(\begin{cases}b=-a(x_1+x_2+x_3) \\ c=a(x_1x_2+x_2x_3+x_3x_1) \\ d=-ax_1x_2x_3\end{cases}\),即 \(\begin{cases}x_1+x_2+x_3=-\frac{b}{a} \\ x_1x_2+x_2x_3+x_3x_1=\frac{c}{a} \\ x_1x_2x_3=-\frac{d}{a} \end{cases}\)。
运用三次方程韦达定理,我们可以快速解决一些代数问题。
例7:已知 \(x_1,x_2,x_3\) 分别为方程 \(x^3-x^2-1=0\) 的根,计算 \(\frac{1+x_1}{1-x_1}+\frac{1+x_2}{1-x_2}+\frac{1+x_3}{1-x_3}\) 的值。
解析:
\[\begin{aligned} &\frac{1+x_1}{1-x_1}+\frac{1+x_2}{1-x_2}+\frac{1+x_3}{1-x_3} \\ =& \frac{2}{1-x_1}-1+\frac{2}{1-x_2}-1+\frac{2}{1-x_3}-1 \\ =& 2\left(\frac{1}{1-x_1}+\frac{1}{1-x_2}+\frac{1}{1-x_3}\right)-3 \\ =& 2\left[\frac{(1-x_2)(1-x_3)+(1-x_1)(1-x_3)+(1-x_1)(1-x_2)}{(1-x_1)(1-x_2)(1-x_3)}\right]-3 \\ =& 2\left[\frac{3+(x_1x_2+x_2x_3+x_3x_1)-2(x_1+x_2+x_3)}{1-x_1x_2x_3+(x_1x_2+x_2x_3+x_3x_1)-(x_1+x_2+x_3)}\right]-3 \end{aligned}\]因为 \(x_1,x_2,x_3\) 分别为方程 \(x^3-x^2-1=0\) 的根,所以
\[\begin{cases}x_1+x_2+x_3=1 \\ x_1x_2+x_2x_3+x_3x_1=0 \\ x_1x_2x_3=1 \end{cases} \]代入原式 \(= 2 \times(\frac{3+0-2}{1-1+0-1})-3=-5\)。
三次函数的图像与性质
形
用几何画板画出 \(f(x)=(x-1)(x-2)(x-3)\) 的图像如图。

能够发现,一个普通的三次函数有最多 \(3\) 个零点(可能有两个或者一个零点),\(2\) 个顶点(可能没有顶点),\(1\) 个对称中心。如果设这个三次函数的两个顶点为 \(A(x_1,y_1)\) 和 \(B(x_2,y_2)\)。
当三次项系数 \(a>0\) 时:
- 该函数在 \((-\infty,x_1]\) 中单调递增;
- 该函数在 \((x_1,x_2]\) 中单调递减;
- 该函数在 \((x_2,+\infty)\) 中单调递增。
当三次项系数 \(a<0\) 时:
- 该函数在 \((-\infty,x_1]\) 中单调递减;
- 该函数在 \((x_1,x_2]\) 中单调递增;
- 该函数在 \((x_2,+\infty)\) 中单调递减。
数
顶点
我们知道三次函数 \(f(x)=ax^3+bx^2+cx+d(a \ne 0)\) 的导数是 \(f'(x)=3ax^2+2bx+c\)。导数反映了一个函数在某一点处的变化率。那么如果一个函数在某一点的变化率等于 \(0\),那么这一点就是原函数的顶点。
那么我们令 \(f'(x)=3ax^2+2bx+c=0\),计算 \(\Delta=(2b)^2-4\times(3a)\times c=4b^2-12ac\)。
也就是说,当 \(\Delta>0\) 时,即 \(b^2-3ac>0\) 时,原函数有 \(2\) 个顶点;当 \(\Delta \leq 0\) 时,即 \(b^2-3ac \leq 0\) 时,原函数没有顶点。
如果 \(\Delta>0\),我们能够求出函数顶点的两个横坐标:
顺便我们也求出来了原函数存在两个顶点的充要条件,就是 \(b^2-3ac>0\)。求出顶点,单调性啥的就很好说了。
对称中心
一个三次函数的对称中心就是两个顶点的中点。如果我们代入公式,计算
看起来和二次函数的对称轴公式很像。把对称中心的横坐标求出来,代入原函数就是对称中心的纵坐标了。
计算一元三次方程的近似根
在计算近似根前的操作
我们计算近似根,首先要知道这个方程的根的分布是什么样的。为了论述简单,我们只考虑三次项系数为正数的情况,如果是负数,那么可以先让等式两边同时乘以 \(-1\) 即可。
我们不妨先把顶点求出来,拿出公式:
-
如果 \(b^2-3ac<0\),那么函数 \(f(x)=ax^3+bx^2+cx+d\) 不存在顶点,也就是说这个函数在 \((-\infty,\infty)\) 是单调的,只能有 \(1\) 个零点;
-
如果 \(b^2-3ac=0\),回顾“配立方法”,这个是这个三次方程能够配立方的情形,因此只有一个实数 \(x\) 满足方程,也只能有 \(1\) 个零点。
-
如果 \(b^2-3ac>0\),也就是原函数有两个顶点 \((x_1,f(x_1)),(x_2,f(x_2))\),根据这种三次函数的单调性有 \(f(x_1)>f(x_2)\)(因为我们钦定三次项系数为正数),这个时候需要讨论两个顶点关于 \(0\) 的大小关系,根据零点存在性定理可得到以下结论:
- 如果 \(f(x_1)>f(x_2)> 0\),那么原函数只有 \(1\) 个零点,在区间 \((-\infty,x_1)\) 中;
- 如果 \(f(x_1)>0=f(x_2)\),那么原函数有 \(2\) 个零点,一个在区间 \((-\infty,x_1)\) 中,另一个为 \(x_2\);
- 如果 \(f(x_1)>0>f(x_2)\),那么原函数有 \(3\) 个零点,分别在区间 \((-\infty,x_1),(x_1,x_2),(x_2,+\infty)\) 中;
- 如果 \(f(x_1)=0>f(x_2)\),那么原函数有 \(2\) 个零点,一个在区间 \((x_2,+\infty)\) 中,另一个为 \(x_1\);
- 如果 \(0>f(x_1)>f(x_2)\),那么原函数有 \(1\) 个零点,在区间 \((x_2,+\infty)\) 中;
零点存在性定理:设函数是 \([a,b]\) 上的连续函数,且存在不等式 \(f(a)f(b)<0\),则在 \((a,b)\) 上,至少存在一个数 \(x\) ,能够使得 \(f(x)=0\) 成立。
至此我们只需要解决在一个区间上有且只有一个零点的情况了。
二分法
二分法是求近似根比较基础的方法,易于理解。
原理:零点存在性定理。
步骤:首先选取一个区间 \([a,b]\),要求函数在区间 \([a,b]\) 已经被确定有且仅有一个零点,并提前预设一个精度 \(\varepsilon\)。
- 取 \([a,b]\) 的中点 \(m=\frac{a+b}{2}\)。
- 如果 \([a,b]\) 的精度已经满足要求(也就是 \(|b-a|<\varepsilon\)),那么 \(m\) 就可以作为我们要求的近似根。否则比较 \(f(a)f(m)\) 与 \(0\) 的大小关系。
- 如果 \(f(a)f(m)>0\),令 \(a \leftarrow m\)。
- 如果 \(f(a)f(m)<0\),令 \(b \leftarrow m\)。
- 重复 1. 2. 的操作即可。
牛顿迭代法
牛顿迭代法是求近似根较为常用的方法,其特点是方法简单,收敛速度快。但前提是能够知道原函数的导数。每迭代计算一次,牛顿迭代法结果的有效数字将增加一倍。
原理
对于一个函数 \(f(x)\),其导数 \(f'(x)\) 的几何意义之一是函数 \(f(x)\) 上的点 \((x,f(x))\) 切线方程的斜率。
所以对于函数上的一个点 \((x_0,f(x_0))\),我们能够写出它的切线方程:\(f'(x_0)=\frac{y-f(x_0)}{x-x_0}\),这个方程与 \(x\) 轴的交点为 \((x_0-\frac{f(x_0)}{f'(x_0)},0)\),如果我们令 \(x_1=x_0-\frac{f(x_0)}{f'(x_0)}\),那么点 \((x_1,f(x_1))\) 相较于 \((x_0,f(x_0))\) 会更接近函数的零点。如图所示。浅蓝色为 \(f(x)\) 的图像。
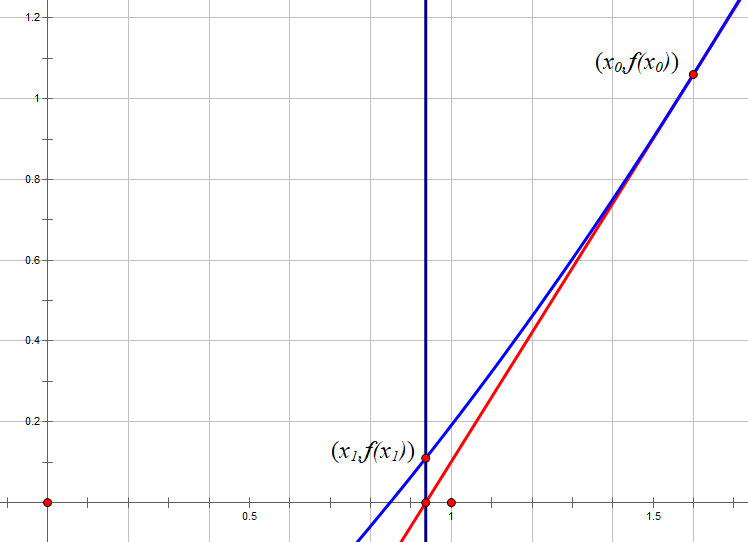
步骤
步骤就很简单了,对于区间 \([a,b]\),取 \(x_0=\frac{a+b}{2}\)(这个 \(x_0\) 只要在区间内且 \(f'(x_0)\) 不为 \(0\) 即可)。
然后每次计算:
一直迭代下去即可得到精确的答案。
例8:分别用二分法、牛顿迭代法求方程 \(x^3-3x+1=0\) 在 \((0,1)\) 之间的近似根。
解析:以下表格是用二分法的过程
迭代次数 \(a\) \(b\) \(m\) \(f(m)\) 新区间 $ 0$ $ 0 $ $1 $ \(0.5\) \(-0.375\) \([0,0.5]\) $1 $ \(0\) $ 0.5$ \(0.25\) \(0.2656\) \([0.25,0.5]\) $ 2 $ $ 0.25$ $0.5 $ \(0.375\) \(-0.0723\) \([0.25,0.375]\) $ 3 $ \(0.25\) \(0.375\) \(0.3125\) \(0.0930\) \([0.3125,0.375]\) 迭代 \(3\) 次只能保证小数点后 \(2\) 位的精度。
在牛顿迭代法中,我们计算 \(f'(x)=3x-3\)。这个是使用牛顿迭代法的结果。
迭代次数 \(x_n\) \(f(x_n)\) \(f'(x_n)\) \(x_{n+1}\) \(0\) \(0.500000\) \(-0.375000\) \(-2.250\) \(0.333333\) \(1\) \(0.333333\) \(0.037037\) \(-2.667\) \(0.347222\) \(2\) \(0.347222\) \(-0.000365\) \(-2.638\) \(0.347296\) \(3\) \(0.347296\) \(-3.7×10^{-8}\) \(-2.638\) \(0.347296\) 迭代 \(3\) 次即能获得小数点后 \(6\) 位的精度。效率较高。




 浙公网安备 33010602011771号
浙公网安备 33010602011771号