2021~2022 上学期水题选做

P2051 [AHOI2009] 中国象棋

同一行或者同一列最多放两个棋子。于是可以设 \(f_{i,j,k}\) 表示前 \(i\) 行有 \(j\) 列放一个棋子，\(k\) 列放两个棋子的答案。

转移时分类讨论：

第 \(i\) 行不放棋子；
第 \(i\) 行放一个棋子；
1. 在原来没有放棋子的列上放棋子；
2. 在原来放了一个棋子的列上放棋子；
第 \(i\) 行放两个棋子；
1. 在原来没有放棋子的列上放两个棋子；
2. 在原来没有放棋子的列上放一个棋子，在原来放了一个棋子的列上放一个棋子；
3. 在原来放了一个棋子的列上放两个棋子。

P2018 消息传递

这个题面好像没说清楚，其实一个时刻最多只能做一次传递。

对于每一个 \(i\)，我们要考虑整个树以 \(i\) 为根的答案。

设 \(f_u\) 表示以 \(u\) 为根的子树的答案，由于我们要考虑每个 \(v\) 被传递的顺序，所以：

\[f_u=\max_{v\in\operatorname{son}(u)}\{f_v+a_v\} \]

\(a_v\) 表示 \(v\) 被选的顺序。

如何确定这个顺序？贪心的让大的 \(f_v\) 匹配小的 \(a_v\) 即可。

P3574 [POI2014] FAR-FarmCraft

和上一道题类似。也是要考虑进入子树顺序的树形 dp。

P4742 [Wind Festival] Running In The Sky

缩点 + DAGdp。

P3622 [APIO2007] 动物园

设 \(f_{i,S}\) 表示前 \(i\) 个围栏，\(\{i,i+1,i+2,i+3,i+4\}\) 是否放动物的集合为 \(S\) 时的答案。

转移时记录 \(cnt_{i,S}\) 表示 \(\{i,i+1,i+2,i+3,i+4\}\) 是否放动物的集合为 \(S\) 时有多少人会满意即可。

但是这是一个环上的问题而且断环为链行不通，怎么处理呢？

先枚举一个 \(S\) 表示第 \(0\sim 4\) 个围栏是否放动物的集合，然后令 \(f_{0,i}=-\infty,f_{0,S}=0\)，并 dp 一遍，最后将 \(f_{n,S}\) 统计进答案。这样一来因为第 \(0\) 个围栏和第 \(n\) 个围栏的状态一样，所以这就相当于变成环了。

P4216 [SCOI2015] 情报传递

转化一下题意：

操作 1：设当前是第 \(i\) 次操作，你要求出 \(u\leftrightarrow v\) 的路径上满足 \(i-a_w\gt c\) 的 \(w\) 的个数。
操作 2：设当前是第 \(i\) 次操作，将点 \(u\) 打上一个时间戳 \(a_u=i\)。

然后我们要找一个能求链上 \(\le x\) 的数的个数的数据结构，使用可持久化权值线段树即可。

CF414C Mashmokh and Reverse Operation

翻转时，每个块对其它块没有影响，块内就是顺序对和逆序对交换。

维护一下每层的顺序对和逆序对即可。

CF522D Closest Equals

记录 \(pre_i\) 表示离 \(a_i\) 最近的 \(a_j=a_i\) 的 \(j\)，\(dis_i=i-pre_i\)。

将询问离线按右端点排序，边扫边维护 \(dis_{pre_i}\)（注意是 \(pre_i\)，这样才能保证询问时询问到的每一对 \([pre_i,i]\) 都在 \([l,r]\) 内）的最小值即可。

P1641 [SCOI2010] 生成字符串

考虑排除法。所有 \(\tt{01}\) 串有 \(\binom{n+m}m\) 个，不符合条件的 \(\tt{01}\) 串有 \(\binom{n+m}{m-1}\) 个，为什么？

对于一个不合法的串，找到第一个不合法的位置（即 \(\tt 1\) 的个数大于 \(\tt 0\) 的个数），把它后面的部分反转，这样就得到了一个 \(n+1\) 个 \(\tt 1\) 和 \(m-1\) 个 \(\tt 0\) 的字符串。

同理，每一个 \(n+1\) 个 \(\tt 1\) 和 \(m-1\) 个 \(\tt 0\) 的字符串都可以对应一个不合法的串。

这样它们之间构成了一一映射，方案数就是 \(\binom{n+m}{m-1}\)。

P4342 [IOI1998] Polygon

断环为链然后区间 dp。设 \(f_{i,j}\) 表示只考虑 \([i,j]\) 这个区间时的答案。

然而由于负负得正，所以我们还要记录一个 \(g_{i,j}\) 表示对 \([i,j]\) 这个区间进行操作得到结果的最小值。

P2532 [AHOI2012] 树屋阶梯

设 \(f_i\) 表示 \(n=i\) 时的答案。我们来证明 \(f_i\) 就是卡特兰数。

首先 \(i\) 个矩形必然各占一个角，否则有一个矩形就会占着两个角，矛盾。

我们考虑那个占着左下角的矩形：

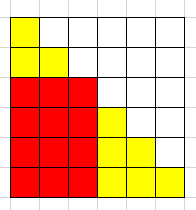
可以看出：

\[f_i=\sum_{j=0}^{i-1}f_jf_{i-j-1} \]

于是 \(f_i\) 是卡特兰数。

P1032 [NOIP2002 提高组] 字串变换

深搜 + 迭代加深。

CF149D Coloring Brackets

设 \(f_{l,r,i,j}\) 表示当 \(s_l\sim s_r\) 是合法括号串，且 \(s_l\) 颜色为 \(i\)，\(s_r\) 颜色为 \(j\) 时的答案。

那么当 \(s_l,s_r\) 刚好配对时，\(f_{l,r}\) 就从 \(f_{l+1,r-1}\) 转移过来。当 \(s_l=\texttt(,s_r=\texttt)\) 时，这个串应该是 \(\texttt(\cdots\texttt)\texttt(\cdots\texttt)\) 这个样子的。\(f_{l,r}\) 就从 \(f_{l,p},f_{p+1,r}\) 转移过来。

UVA1630 串折叠 Folding

区间 dp 模板。

P2400 秘密文件

上一题双倍经验。

CF1144F Graph Without Long Directed Paths

如果有答案，那么这个图一定是一个二分图。

二分图染色即可。

P1126 机器人搬重物

比较难写的 BFS。

P5588 小猪佩奇爬树

分情况讨论：

若颜色 \(i\) 不存在，则答案为 \(\frac{n(n-1)}2\)。
若颜色 \(i\) 在结点 \(u\) 出现了一次，那么答案就是把这个结点所有子树的大小互相乘然后加起来。
若颜色 \(i\) 出现了 \(\ge 2\) 次，那么这些结点必须在一条链上。此时答案为链两端结点子树的大小相乘。

P2491 [SDOI2011] 消防

答案一定在直径上。如果不在，由于绿色部分的长度大于蓝色部分的长度，如果选的是蓝色部分和黑色部分，则答案更劣。

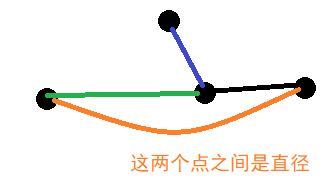
在直径上双指针 \(+\) 单调队列维护 \(\max dis\) 即可。

CF609E Minimum spanning tree for each edge

先求出原图的 MST，然后对于每条边分树边和非树边讨论即可。

CF1096F Inversion Expectation

分类讨论：

已知数与已知数形成的逆序对：树状数组统计。
已知数与未知数形成的逆序对：对于每一个 \(i\)，设未知数数量为 \(m\)，\(\lt a_i\) 的未知数数量为 \(lt_i\)，在 \(i\) 右边的未知数数量为 \(r_i\)，则每一个未知数形成逆序对的概率为 \(\frac{lt_i}m\)，总的期望为 \(\frac{r_ilt_i}m\)。
未知数与已知数形成的逆序对：与 2 类似。
未知数与未知数形成的逆序对：每一对都有 \(\frac12\) 的概率成为逆序对，总的期望为 \(\frac{m(m-1)}2\cdot \frac12=\frac{m(m-1)}4\)。

CF1110F Nearest Leaf

题解

P3644 [APIO2015] 八邻旁之桥

把每个人拆成两个点（起点 \(s_i\) 和终点 \(t_i\)）来考虑，这样一个人走的路程就是两条线段。

\(k=1\) 时显然。

\(k=2\) 时，将所有人按 \(s_i+t_i\) 排序，枚举分界点，位于左边的走左边的桥，右边的走右边的桥，于是就成了两个 \(k=1\) 的问题，用平衡树维护即可。

CF780F Axel and Marston in Bitland

倍增 Floyd。设 \(f_{0/1,j,u,v}\) 表示以 \(0/1\) 为第一条边，路径长度为 \(2^j\)，是否存在 \(u\to v\) 的路径。注意到直接 dp 是 \(\mathcal O(n^3\log 10^{18})\) 的，会超时，所以要 std::bitset 优化。

dp 之后还要贪心的取路径。倒着枚举 \(j=\log 10^{18},\cdots,0\)，如果能取就取。

CF865D Buy Low Sell High

反悔贪心。

一个显然的想法是低价买入高价卖出。但是后面也许有更高价。这时就需要反悔。

P2949 [USACO09OPEN] Work Scheduling G

反悔贪心。

先按规定时间排序，如果有时间就做。如果没时间就反悔：把之前做过的一个价值较小的工作不要了，然后再做这个工作。

P1230 智力大冲浪

上一题双倍经验。

P4053 [JSOI2007] 建筑抢修

现在这个题是时间不一样价值一样。

先按规定时间排序，如果有时间就做。如果没时间就反悔：把之前做过的一个用时较长的工作不要了，然后再做这个工作。

P5410【模板】扩展 KMP（Z 函数）

题解

UVA11475 Extend to Palindrome

让中间红色部分的长度最大即可。

令 \(t=s^R+\texttt{#}+s\)，\(s^R\) 是 \(s\) 翻转后的串。对 \(t\) 使用 Z 算法。那么找到下图中的红色部分即可。

CF432D Prefixes and Suffixes

建出失配树，那么根据失配树的性质，一个长度为 \(p\) 的 border（如果存在）的出现次数就是树上以 \(p\) 为根的子树的大小。

UVA11022 String Factoring

经典区间 dp 题。转移不多说了。

要注意的是判断循环时要用 KMP 做，时间复杂度 \(\mathcal O(n^3)\)。

CF126B Password

跑一遍 KMP，要求的字符串的长度只可能是 \(nxt_n,nxt_{nxt_n},nxt_{nxt_{nxt_{n}}},\cdots\)（这些是字符串所有 border 的长度）。

维护一个桶，记录的是 \(nxt_1,nxt_2,\cdots,nxt_{n-1}\) 的出现次数，那么我们从 \(n\) 开始跳 \(nxt\)，看看这些长度有没有在桶里出现过即可。

UVA455 周期串 Periodic Strings

结论：对于一个 \(i\)，\(n-nxt_i\) 一定是字符串的周期（不一定是完整的，例如 \(\texttt{ab}\) 是 \(\texttt{aba}\) 的周期，但不是 \(\texttt{abc}\) 的周期）。

对于这个题，只需求满足 \(n-nxt_i\mid n\) 即可。

P4556 [Vani有约会] 雨天的尾巴 /【模板】线段树合并

题解

P4197 Peaks

将询问离线，按 \(x\) 排序。那么我们可以一边把 \(\le x\) 的边加进来，一边处理询问。

加边的时候涉及到合并连通块的问题，可以使用权值线段树合并。

P1456 Monkey King

模板题。

P1552 [APIO2012] 派遣

可以发现这个题有子结构。对于一棵树，我们将先算出它所有子树的答案，然后合并。合并的时候，我们要尽可能少的踢人，踢掉工资最大的即可。

用可并堆或者线段树合并实现均可。

P4819 [中山市选] 杀人游戏

先缩点。设缩点后图中入度为 \(0\) 的点有 \(cnt\) 个。

显然，我们只需要问这些连通块里的任意一个人就行了，答案为 \(1-\frac{cnt}{n}\)。

不过还没有完，如果一个连通分量入度为 \(0\) 且里面只有一个点，且去掉该点后与这个点直接相连的点均有入度，那么我们就可以通过得到其它 \(n-1\) 个人的身份而推出这个人的身份，也就是说不用问这个点，答案为 \(1-\frac{cnt-1}{n}\)。

P3899 [湖南集训] 谈笑风生

分两种情况讨论：

如果 \(b\) 是 \(a\) 的祖先，那么 \(b\) 有 \(\min(k,dep_a-1)\) 种选择，\(c\) 有 \(siz_a-1\) 种选择（因为 \(c\) 必须在 \(a\) 的子树里），总共有 \(\min(k,dep_a-1)\cdot (siz_a-1)\) 种选择。
如果 \(b\) 在 \(a\) 的子树里，那么 \(b\) 必须满足 \(1\le dep_b-dep_a\le k\)，\(c\) 在 \(b\) 的子树里。这时可以把它抽象为一个二维数点问题：给定平面上 \(n\) 个点 \((dfn_i,dep_i)\)，权值为 \(siz_i-1\)，求满足 \(dfn_i\in[dfn_a,dfn_a+siz_a-1]\) 且 \(dep_i\in[dep_a+1,dep_a+k]\) 的点的权值和。可以用可持久化权值线段树实现。

CF1000E We Need More Bosses

答案就是缩点后树的直径。

CF1009F Dominant Indices

设 \(f_{u,i}\) 表示以 \(u\) 为根的子树中到 \(u\) 距离为 \(i\) 的点的个数，则：

\[f_{u,i}=\sum_{v\in\operatorname{son}(u)}f_{v,i-1} \]

线段树合并可以用于一些树形 dp 的优化。我们可以考虑线段树合并，此时为了方便我们要改一下状态：\(f_{u,i}\) 表示以 \(u\) 为根的子树中深度为 \(i\) 的点的个数。此时有：

\[f_{u,i}=\sum_{v\in\operatorname{son}(u)}f_{v,i} \]

这样就可以线段树合并了。

CF208E Blood Cousins

可持久化权值线段树模板。

P3521 [POI2011] ROT-Tree Rotations

有一种用线段树合并求逆序对的办法：

随便搞一颗二叉树，使得它的中序遍历为 \(a_1,a_2,\cdots,a_n\)。

一开始我们有 \(n\) 棵值域线段树，第 \(i\) 棵树中把 \(a_i\) 的值设为 \(1\)（即 modify(root,1,n,a[i],1)）。

DFS 这棵树。遍历到一个结点时，我们要做的事情是合并左右子树对应的两棵值域线段树，并统计答案：

Code

int merge(int i,int j,int l,int r){
  if(!i||!j)return i+j;
  if(l==r)return t[i].v+=t[j].v,i;
  int mid=(l+r)>>1;
  ans+=1LL*t[rs(i)].v*t[ls(j)].v; // 为什么？
  ls(i)=merge(ls(i),ls(j),l,mid);
  rs(i)=merge(rs(i),rs(j),mid+1,r);
  pushUp(i);
  return i;
}

对于本题，在线段树合并的时候，统计交换左右子树有对少个逆序对，不交换有多少逆序对，两者取最小值即可。实现与以上代码类似。

P3960 [NOIP2017 提高组] 列队

当我们对一个学生操作后，要改变的只有他原来所在行和最后一列。

那我们可以用 \(n+1\) 棵平衡树来为维护每一行的情况和最后一列的情况。具体操作如下：

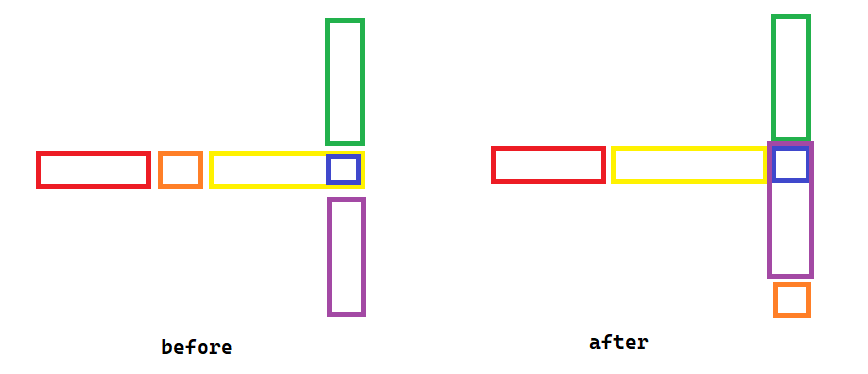
但是还没完！如果真要把所有学生代表的结点开出来，那是不可能的！

我们只能把编号连续的学生作为一段来开点。这样一来，在分裂的时候就会出现将一个点裂成两个点的情况：

Code

struct Node{
  ll l,r,siz; // l, r 即这个结点表示编号为 l 的学生到编号为 r 的学生
  int ls,rs,w;
  Node(){}
  Node(ll _l,ll _r):l(_l),r(_r),siz(_r-_l+1),w(rand()),ls(0),rs(0){}
  inline ll len(){return r-l+1;}
};

void split(int rt,ll k,int &x,int &y){
  if(!rt)return x=y=0,void();
  if(t[ls(rt)].siz+t[rt].len()<=k){
    x=rt;
    split(rs(rt),k-(t[ls(rt)].siz+t[rt].len()),rs(x),y);
    pushUp(rt);
  }else if(t[ls(rt)].siz<k){ // 裂点
    ll L=t[rt].l,M=L+(k-t[ls(rt)].siz)-1,R=t[rt].r;
    x=newNode(L,M),y=newNode(M+1,R);
    ls(x)=ls(rt),rs(y)=rs(rt);
    pushUp(x),pushUp(y);
  }else{
    y=rt;
    split(ls(rt),k,x,ls(y));
    pushUp(rt);
  }
}

CF487E Tourists

相当于把树剖强行上图：建圆方树，在圆方树上树剖。

要注意的是在修改时不能修改一个点周围的所有方点，这样复杂度有问题。应该对于每个方点开一个维护它儿子最小值的 std::multiset，这样修改的时候就只需要修改它父亲的 std::multiset 了。

P1600 [NOIP2016 提高组] 天天爱跑步

考虑每个玩家对观察员的贡献。

分两种情况：

考虑路径 \(s_i\to \operatorname{LCA}(s_i,t_i)\)。此时若一个观察员 \(j\) 满足 \(dep_{s_i}-dep_j=w_j\)，即 \(dep_{s_i}=dep_j+w_j\) 时；则玩家 \(i\) 对观察员 \(j\) 有贡献。
考虑路径 \(\operatorname{LCA}(s_i,t_i)\to t_i\)。此时若一个观察员 \(j\) 满足 \(\operatorname{dist}(s_i,t_i)-(dep_{t_i}-dep_j)=w_j\)，即 \(\operatorname{dist}(s_i,t_i)-dep_{t_i}=w_j-dep_j\) 时；则玩家 \(i\) 对观察员 \(j\) 有贡献。

以情况 1 为例，我们可以将路径 \(s_i\to \operatorname{LCA}(s_i,t_i)\) 上的所有点都放一个编号 \(dep_{s_i}\) 的物品。对整棵树 DFS，每遍历到一个点 \(u\)，就将 \(ans_u\) 加上 \(u\) 上编号 \(dep_j+w_j\) 物品的数量。可以用树上差分 + 桶实现。

P4213 【模板】杜教筛（Sum）

题解

P3768 简单的数学题

先按照套路推式子：

推式子

\[\begin{aligned} &\sum_{i=1}^n\sum_{j=1}^nij\gcd(i,j)\\ =&\sum_{i=1}^n\sum_{j=1}^nij\sum_{d\mid\gcd(i,j)}\varphi(d)\\ =&\sum_{d=1}^n\varphi(d)\sum_{i=1}^{\left\lfloor\frac nd\right\rfloor}\sum_{j=1}^{\left\lfloor\frac nd\right\rfloor}id\cdot jd\\ =&\sum_{d=1}^nd^2\varphi(d)\sum_{i=1}^{\left\lfloor\frac nd\right\rfloor}\sum_{j=1}^{\left\lfloor\frac nd\right\rfloor}ij \end{aligned} \]

于是我们得到，\(\mathrm{original\ formula}=\sum_{d=1}^nd^2\varphi(d)h\left(\left\lfloor\frac nd\right\rfloor\right)\)，其中 \(h(n)=\sum_{i=1}^n\sum_{j=1}^nij=\frac{n^2(n+1)^2}4\)。

\(h\) 的那部分可以用数论分块处理，接下来我们考虑 \(f(n)=n^2\varphi(n)\)，令 \(g(n)=n^2\)，则：

\[(f*g)(n)=\sum_{d\mid n}d^2\varphi(d)\cdot \left(\frac nd\right)^2=n^2\sum_{d\mid n}\varphi(d)=n^3 \]

\[\sum_{i=1}^n(f*g)(i)=\sum_{i=1}^ni^3=\frac{n^2(n+1)^2}4 \]

于是就可以杜教筛了。

P4449 于神之怒加强版

令 \(n\le m\)。

先推式子

\[\begin{aligned}&\sum_{i=1}^n\sum_{j=1}^m\gcd(i,j)^k\\=&\sum_{d_1=1}^nd_1^k\sum_{i=1}^n\sum_{j=1}^m[\gcd(i,j)=d_1]\\=&\sum_{d_1=1}^nd_1^k\sum_{i=1}^{\left\lfloor\frac n{d_1}\right\rfloor}\sum_{j=1}^{\left\lfloor\frac m{d_1}\right\rfloor}[\gcd(i,j)=1]\\=&\sum_{d_1=1}^nd_1^k\sum_{i=1}^{\left\lfloor\frac n{d_1}\right\rfloor}\sum_{j=1}^{\left\lfloor\frac m{d_1}\right\rfloor}\sum_{d_2\mid\gcd(i,j)}\mu(d_2)\\=&\sum_{d_1=1}d_1^k\sum_{d_2=1}^{\left\lfloor\frac n{d_1}\right\rfloor}\mu(d_2)\left\lfloor\frac n{d_1d_2}\right\rfloor\left\lfloor\frac m{d_1d_2}\right\rfloor\end{aligned} \]

根据做题经验，此时我们应该令 \(T=d_1d_2\)，于是：

\[\begin{aligned}&\sum_{i=1}^n\sum_{j=1}^m\gcd(i,j)^k\\=&\sum_{T=1}^n\left\lfloor\frac nT\right\rfloor\left\lfloor\frac mT\right\rfloor\sum_{d\mid T}d^k\mu\left(\frac Td\right)\end{aligned} \]

然后发现前面的那部分可以整除分块。对于右边的部分，令 \(f(n)=\sum_{d\mid n}d^k\mu\left(\frac nd\right)=(id_k*\mu)(n)\)，它是一个积性函数，故可以线性筛：

\[\begin{cases} f(p)=p^k-1,&p\in\mathbb P\\ f(ij)=f(i)\cdot j^k,&j\in \mathbb P,j\mid i\\ f(ij)=f(i)\cdot (j^k-1),&j\in\mathbb P,j\nmid i \end{cases} \]

P3704 [SDOI2017] 数字表格

令 \(n\le m\)。

先推式子

\[\begin{aligned} &\prod_{i=1}^n\prod_{j=1}^mf_{\gcd(i,j)}\\ =&\prod_{d=1}^nf_d^{\sum_{i=1}^n\sum_{j=1}^m[\gcd(i,j)=d]}\\ =&\prod_{d=1}^nf_d^{\sum_{i=1}^{\lfloor n/d\rfloor}\sum_{j=1}^{\lfloor m/d\rfloor}[\gcd(i,j)=1]}\\ =&\prod_{d_1=1}^nf_{d_1}^{\sum_{d_2=1}^n\mu(d_2)\left\lfloor\frac n{d_1d_2}\right\rfloor\left\lfloor\frac m{d_1d_2}\right\rfloor}\\ =&\prod_{T=1}^n\prod_{d\mid T}f_d^{\mu\left(\frac Td\right)\left\lfloor\frac nT\right\rfloor\left\lfloor\frac mT\right\rfloor}\\ =&\prod_{T=1}^n\left(\prod_{d\mid T}f_d^{\mu\left(\frac Td\right)}\right)^{\left\lfloor\frac nT\right\rfloor\left\lfloor\frac mT\right\rfloor} \end{aligned} \]

外面一层 \(\left\lfloor\frac nT\right\rfloor\left\lfloor\frac mT\right\rfloor\) 直接整除分块，里面一层 \(\prod_{d\mid T}f_d^{\mu\left(\frac Td\right)}\) 可以暴力预处理：将每个数乘到它的倍数里。

P3172 [CQOI2015] 选数

First, create an easy problem.
Second, add \(\gcd=k\).
Then you'll get a CQOI.

推式子

\[\begin{aligned}&\sum_{i_1=L}^H\sum_{i_2=L}^H\cdots\sum_{i_N=L}^H[\gcd(i_1,i_2,\cdots,i_N)=K]\\=&\sum_{i_1=\left\lfloor\frac{L-1}K\right\rfloor+1}^{\left\lfloor\frac HK\right\rfloor}\sum_{i_2=\left\lfloor\frac{L-1}K\right\rfloor+1}^{\left\lfloor\frac HK\right\rfloor}\cdots\sum_{i_N=\left\lfloor\frac{L-1}K\right\rfloor+1}^{\left\lfloor\frac HK\right\rfloor}[\gcd(i_1,i_2,\cdots,i_N)=1]\\\end{aligned} \]

令 \(H\gets \left\lfloor\frac HK\right\rfloor\)，\(L\gets\left\lfloor\frac{L-1}K\right\rfloor+1\)，则原式化为：

\[\begin{aligned} =&\sum_{i_1=L}^H\sum_{i_2=L}^H\cdots\sum_{i_N=L}^H[\gcd(i_1,i_2,\cdots,i_N)=1]\\ =&\sum_{i_1=L}^H\sum_{i_2=L}^H\cdots\sum_{i_N=L}^H\sum_{d\mid\gcd(i_1,i_2,\cdots,i_N)}\mu(d)\\ =&\sum_{d=1}^H\mu(d)\left(\left\lfloor\frac Hd\right\rfloor-\left\lfloor\frac{L-1}d\right\rfloor+1\right)^K \end{aligned} \]

整除分块即可。

P3312 [SDOI2014] 数表

先不考虑 \(\le a\) 这个条件：

推式子

设 \(f(n)=\sum_{d\mid n}d\)。并令 \(n\le m\)。

\[\begin{aligned} &\sum_{i=1}^n\sum_{j=1}^mf(\gcd(i,j))\\ =&\sum_{d=1}^nf(d)\sum_{i=1}^n\sum_{j=1}^m[\gcd(i,j)=d]\\ =&\sum_{d=1}^nf(d)\sum_{i=1}^{\left\lfloor\frac nd\right\rfloor}\sum_{j=1}^{\left\lfloor\frac md\right\rfloor}[\gcd(i,j)=1]\\ =&\sum_{d_1=1}^nf(d_1)\sum_{d_2=1}^{\left\lfloor\frac n{d_1}\right\rfloor}\mu(d_2){\left\lfloor\frac n{d_1d_2}\right\rfloor}{\left\lfloor\frac m{d_1d_2}\right\rfloor}\\ =&\sum_{T=1}^n\left\lfloor\frac nT\right\rfloor\left\lfloor\frac mT\right\rfloor\sum_{d\mid T}f(d)\mu\left(\frac Td\right) \end{aligned} \]

然后考虑 \(f(d)\le a\) 这个条件。我们可以先将询问按 \(a\) 排序，然后一个一个将 \(f(d)\le a\) 的 \(f(d)\mu\left(\frac Td\right)\) 加到树状数组里。