AtCoder Beginner Contest 253 题解
二模考完了，打场比赛放松身心。
比赛地址：https://atcoder.jp/contests/abc253。
A
模拟。
Code
void mian(){
int a,b,c;
scanf("%d%d%d",&a,&b,&c);
if(a<=b&&b<=c||c<=b&&b<=a)puts("Yes");
else puts("No");
}
B
还是模拟。
Code
void mian(){
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)
scanf("%s",s[i]+1);
int x1=-1,y1=-1,x2=-1,y2=-1;
for(int i=1;i<=n;i++)
for(int j=1;j<=m;j++)
if(s[i][j]=='o'){
if(x1==-1)x1=i,y1=j;
else x2=i,y2=j;
}
printf("%d\n",std::abs(x1-x2)+std::abs(y1-y2));
}
C
又是模拟。
Code
void mian(){
int m;scanf("%d",&m);
std::multiset<int> s;
while(m--){
int opt,x,y;scanf("%d",&opt);
if(opt==1)scanf("%d",&x),s.insert(x);
if(opt==2){
scanf("%d%d",&x,&y);
for(int i=1;i<=y;i++){
auto it=s.find(x);
if(it==s.end())break;
s.erase(it);
}
}
if(opt==3){
printf("%d\n",*(--s.end())-*(s.begin()));
}
}
}
D
小学奥数容斥原理。
Code
ll sum(ll x){
return 1LL*x*(x+1)/2;
}
void mian(){
ll n,a,b;
scanf("%lld%lld%lld",&n,&a,&b);
ll lcm=a/std::__gcd(a,b)*b;
printf("%lld\n",sum(n)-a*sum(n/a)-b*sum(n/b)+lcm*sum(n/lcm));
}
E
dp。设 \(f_{i,j}\) 表示考虑前 \(i\) 项且 \(a_i=j\) 时的答案。则
\[f_{i,j}=\sum_{|j-l|\ge k}f_{i-1,l}
\]
显然可以通过对于每个 \(i\) 处理 \(f_{i,j}\) 的前缀和来优化。
注意特判 \(k=0\) 的情况！
Code
const int P=998244353;
const int N=5000;
int n,m,k,f[N+10][N+10],sum[N+10][N+10];
void mian(){
scanf("%d%d%d",&n,&m,&k);
for(int i=1;i<=m;i++)f[1][i]=1,sum[1][i]=(sum[1][i-1]+1)%P;
for(int i=2;i<=n;i++){
if(k){
for(int j=1;j<=m;j++){
if(j-k>=1)(f[i][j]+=sum[i-1][j-k])%=P;
if(j+k<=m)(f[i][j]+=(sum[i-1][m]-sum[i-1][j+k-1])%P)%=P;
}
}else{
for(int j=1;j<=m;j++)
(f[i][j]+=sum[i-1][m])%=P;
}
for(int j=1;j<=m;j++)
sum[i][j]=(sum[i][j-1]+f[i][j])%P;
}
int ans=0;
for(int i=1;i<=m;i++)
(ans+=f[n][i])%=P;
printf("%d\n",(ans%P+P)%P);
}
F
这题出的不错。
考虑对于一个询问 \((x,y)\)，什么修改操作对它有贡献。
那显然是离它最近且修改的是第 \(x\) 行的那个操作 \(2\) 和这个操作 \(2\) 之后，所有涉及到第 \(y\) 列的操作 \(1\)。
前者开 \(n\) 个 std::vector 维护即可。
对于后者，本质上是有两个轴：时间轴和列轴。这样一来，我们可以以时间轴为要被可持久化的轴，建一棵可持久化线段树，维护区间加、单点查。注意要开标记永久化。
Code
#include<algorithm>
#include<cstdio>
#include<vector>
typedef long long ll;
const int N=2e5;
struct Node{
ll v,lt;
int ls,rs;
};
int n,m,q;
Node t[N<<6];
int rt[N+10],cnt;
std::vector<std::pair<int,int>> vec[N+10];
#define ls(x) (t[x].ls)
#define rs(x) (t[x].rs)
void pushUp(int i,int l,int r){
int mid=(l+r)>>1;
t[i].v=t[ls(i)].v+t[rs(i)].v+t[ls(i)].lt*(mid-l+1)+t[rs(i)].lt*(r-mid);
}
void modify(int &i,int j,int l,int r,int ml,int mr,int d){
i=++cnt;
t[i].v=t[j].v,t[i].lt=t[j].lt;
ls(i)=ls(j),rs(i)=rs(j);
if(ml<=l&&r<=mr){
t[i].lt+=d;
return;
}
int mid=(l+r)>>1;
if(ml<=mid)modify(ls(i),ls(j),l,mid,ml,mr,d);
if(mr>mid) modify(rs(i),rs(j),mid+1,r,ml,mr,d);
pushUp(i,l,r);
}
ll query(int i,int l,int r,int ql,int qr){
if(ql==l&&r==qr)return t[i].v+t[i].lt*(r-l+1);
int mid=(l+r)>>1;
ll tag=(qr-ql+1)*t[i].lt;
if(ql>mid) return tag+query(rs(i),mid+1,r,ql,qr);
if(qr<=mid)return tag+query(ls(i),l,mid,ql,qr);
return tag+query(ls(i),l,mid,ql,mid)+query(rs(i),mid+1,r,mid+1,qr);
}
#undef ls
#undef rs
int main(){
scanf("%d%d%d",&n,&m,&q);
for(int i=1;i<=n;i++)vec[i].push_back({1,0});
for(int i=1;i<=q;i++){
int opt,l,r,x,y;
scanf("%d",&opt);
if(opt==1){
scanf("%d%d%d",&l,&r,&x);
modify(rt[i],rt[i-1],1,m,l,r,x);
}
if(opt==2){
scanf("%d%d",&l,&x);
rt[i]=rt[i-1];
vec[l].push_back({i,x});
}
if(opt==3){
scanf("%d%d",&x,&y);
rt[i]=rt[i-1];
std::pair<int,int> qwq=vec[x].back();
int t=qwq.first,x0=qwq.second;
ll sum=query(rt[i],1,m,y,y)-query(rt[t-1],1,m,y,y);
printf("%lld\n",x0+sum);
}
}
return 0;
}
G
一个比较直接的想法是把两边的“散块”暴力处理（只有 \(\mathcal O(n)\)，所以不会炸），中间的“整块”一起处理。
对于中间的“整块”，可以找规律，如图（取自 官方题解）：
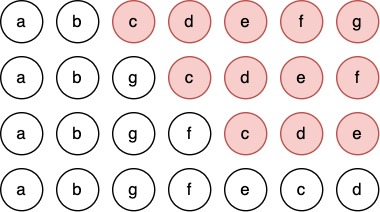
不难发现，设第一次操作交换 \((x_1,y_1)\)，最后一次交换 \((x_2,y_2)\)，这些操作就等价于翻转 \(a_{x_1+1}\sim a_n\) 再翻转 \(a_{x_2}\sim a_n\)。
Code
#include<algorithm>
#include<cstdio>
typedef long long ll;
const int N=2e5;
int n,a[N+10];
ll L,R;
void get(ll t,int &x,int &y){
ll cnt=0;
for(int i=n-1;i>=1;i--){
if(cnt+i>=t){
x=n-i,y=t-cnt+x;
return;
}
cnt+=i;
}
}
int main(){
scanf("%d%lld%lld",&n,&L,&R);
for(int i=1;i<=n;i++)
a[i]=i;
int x1,y1,x2,y2;
get(L,x1,y1);
get(R,x2,y2);
for(int i=y1;i<=n;i++)
std::swap(a[x1],a[i]);
std::reverse(a+x1+1,a+n+1);
std::reverse(a+x2,a+n+1);
for(int i=x2+1;i<=y2;i++)
std::swap(a[x2],a[i]);
for(int i=1;i<=n;i++)
printf("%d%c",a[i]," \n"[i==n]);
return 0;
}
H
状压，设 \(f_{i,S}\) 表示在点集 \(S\) 内连 \(i\) 条边时有多少种森林，则答案就是 \(\frac{f_{i,S}\cdot i!}{m^i}\)。
转移时考虑枚举 \(S\) 的一个子集 \(T\subseteq S\)，让 \(T\) 是一棵树：
\[f_{i,S}=\sum_{T\subseteq S}f_{i-(|T|-1),S\backslash T}\cdot g_T
\]
\(g_S\) 表示仅考虑给集合 \(S\) 中的点连边时有多少种树，这可以用矩阵树定理求。
为了不算重（比如 \(f(\{1\})g(\{2,3\})\) 和 \(f(\{2,3\})g(\{1\})\) 就算重了），我们需要钦定 \(T\) 中必须有某个点 \(v\)（\(v\) 是什么无所谓）。
预处理所有 \(g_S\) 的时间复杂度是 \(\mathcal O(2^nn^3)\)，dp 的时间复杂度是 \(\mathcal O(n3^n)\)，可以通过。
Code
#include<algorithm>
#include<cstdio>
#include<cstring>
#define count(x) __builtin_popcount(x)
const int N=14,M=500;
const int P=998244353;
int n,m,u[M+10],v[M+10];
int a[N+10][N+10],tmpid[N+10];
int f[N+5][1<<N],g[1<<N];
int det(int n){
int res=1;
for(int i=1;i<n;i++)
for(int j=i+1;j<n;j++){
while(a[i][i]){
int r=-a[j][i]/a[i][i];
for(int k=i;k<n;k++)
(a[j][k]+=1LL*r*a[i][k]%P)%=P;
std::swap(a[i],a[j]);res=-res;
}
std::swap(a[i],a[j]);res=-res;
}
for(int i=1;i<n;i++)
res=1LL*res*a[i][i]%P;
return (res%P+P)%P;
}
int qpow(int a,int b){
int res=1;
for(;b;b>>=1,a=1LL*a*a%P)if(b&1)res=1LL*res*a%P;
return res;
}
int inv(int a){
return qpow(a,P-2);
}
int main(){
scanf("%d%d",&n,&m);
for(int i=1;i<=m;i++)
scanf("%d%d",u+i,v+i);
for(int msk=0;msk<(1<<n);msk++){
memset(a,0,sizeof(a));
int cnt=0;
for(int i=1;i<=n;i++)
if((msk>>(i-1))&1)tmpid[i]=++cnt;
for(int i=1;i<=m;i++)
if((msk>>(u[i]-1)&1)&&(msk>>(v[i]-1)&1)){
int uu=tmpid[u[i]],vv=tmpid[v[i]];
a[uu][uu]++,a[vv][vv]++;
a[uu][vv]--,a[vv][uu]--;
}
g[msk]=det(cnt);
}
f[0][0]=1;
for(int msk=0;msk<(1<<n);msk++)
for(int i=0;i<n;i++)
for(int msk2=msk;msk2;msk2=(msk2-1)&msk)
if(msk2&(msk&(-msk))){ // 钦定 msk2 中必须有 lowbit(msk)
int cnt=count(msk2);
if(i-cnt+1>=0)(f[i][msk]+=1LL*f[i-cnt+1][msk^msk2]*g[msk2]%P)%=P;
}
int fac=1,pw=1;
for(int i=1;i<n;i++){
fac=1LL*fac*i%P;
pw=1LL*pw*m%P;
printf("%lld\n",1LL*fac*f[i][(1<<n)-1]%P*inv(pw)%P);
}
return 0;
}
本文来自博客园，作者：registerGen，转载请注明原文链接：https://www.cnblogs.com/registergen/p/abc253_solution.html
浙公网安备 33010602011771号