最大连续子数组--分治法

链接：

给定一个整数数组 nums ，找到一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。

示例:

输入: [-2,1,-3,4,-1,2,1,-5,4],
输出: 6
解释: 连续子数组 [4,-1,2,1] 的和最大，为 6。
进阶:

如果你已经实现复杂度为 O(n) 的解法，尝试使用更为精妙的分治法求解。

 分治解法：

　　对于一个数组 A [ low..high ] , 我们可以将其划分为两个规模相等的子数组A [ low..mid ] 和 A [ mid+1..high ]，其中 mid=(low+high)/2。那么，所有的连续子数组必定位于以下三种位置之一：

　　　　（1）完全位于左子数组中：

　　　　（2）完全位于右子数组中：

　　　　（3）跨越中点：

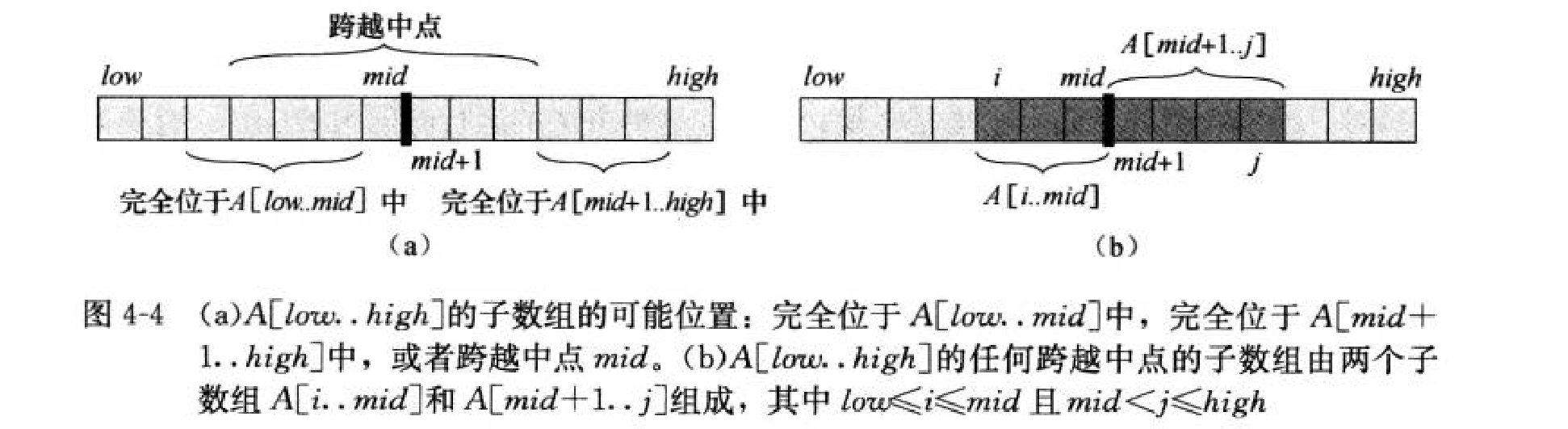
　　因此，我们可以设计一个分治算法来求解这一问题：

　　（1）分解

　　　　如上所述。

　　（2）求解

　　　　当 数组分解到只有一个元素时，那么此时这个必然是最大的连续数组，直接返回这个数组。判断条件便为 low == high。

　　（3）合并

　　　　取 左子数组的最大值、右子数组的最大值、跨越中点的数组的最大值  三者的最大值。

　　　　其中，跨越中点的数组的最大值，需要 O(n) 扫一遍数组。即对每一个递归求解的数组， 先扫一遍中点左边，求出以mid为后缀的 left-max ； 然后扫一遍中点右边，求出以 mid+1 的点为前缀的 right-max，最后返回 （left-max）+（right-max），两者之和即为跨越中点的最大值。

class Solution {
public:
    //分治法
    //合并的部分，注意返回的值是左边加右边的和
    int max_cross_subArray(vector<int> &nums,int low,int mid,int high)
    {
        int left_sum=INT_MIN,right_sum=INT_MIN;
        int sum=0;
        for(int i=mid;i>=low;i--){
            sum+=nums[i];
            left_sum=max(left_sum,sum);
        }
        sum=0;
        for(int i=mid+1;i<=high;i++){
            sum+=nums[i];
            right_sum=max(right_sum,sum);
        }
        return left_sum+right_sum;
    }
    //分治
    int max_subArray(vector<int>&nums,int low,int high)
    {
        if(low==high){
            return nums[low];
        }

        int mid=(low+high)/2;
        
        int left_sum=max_subArray(nums,low,mid);
        int right_sum=max_subArray(nums,mid+1,high);

        int cross_sum=max_cross_subArray(nums,low,mid,high);
        //max
        return max(max(left_sum,right_sum),cross_sum);
    }


    int maxSubArray(vector<int>& nums) {
        int ans=nums[0];
        int left_pos=0,right_pos=0;
        int pre_sum=ans,pre_left=0;

        //分治法
        ans=max_subArray(nums,0,nums.size()-1);
        return ans;
        
    }
};