二分查找技巧---字节跳动2018校招算法方向（第二批）---用户喜好

[编程题]用户喜好

时间限制：3秒

空间限制：262144K

为了不断优化推荐效果，今日头条每天要存储和处理海量数据。假设有这样一种场景：我们对用户按照它们的注册时间先后来标号，对于一类文章，每个用户都有不同的喜好值，我们会想知道某一段时间内注册的用户（标号相连的一批用户）中，有多少用户对这类文章喜好值为k。因为一些特殊的原因，不会出现一个查询的用户区间完全覆盖另一个查询的用户区间(不存在L1<=L2<=R2<=R1)。

输入描述:

输入： 第1行为n代表用户的个数 第2行为n个整数，第i个代表用户标号为i的用户对某类文章的喜好度 第3行为一个正整数q代表查询的组数  第4行到第（3+q）行，每行包含3个整数l,r,k代表一组查询，即标号为l<=i<=r的用户中对这类文章喜好值为k的用户的个数。 数据范围n <= 300000,q<=300000 k是整型

输出描述:

输出：一共q行，每行一个整数代表喜好值为k的用户的个数

输入例子1:

5
1 2 3 3 5
3
1 2 1
2 4 5
3 5 3

输出例子1:

1
0
2

例子说明1:

样例解释:
有5个用户，喜好值为分别为1、2、3、3、5，
第一组询问对于标号[1,2]的用户喜好值为1的用户的个数是1
第二组询问对于标号[2,4]的用户喜好值为5的用户的个数是0
第三组询问对于标号[3,5]的用户喜好值为3的用户的个数是2

解题思路：
刚开始看到题目，觉得是区间查询的题目，于是想线段树、RMQ那些，结果发现查找的k值不能预先存为状态。搜了一下题解发现只是用到二分查找的技巧，看看下图就明白了：

 

 

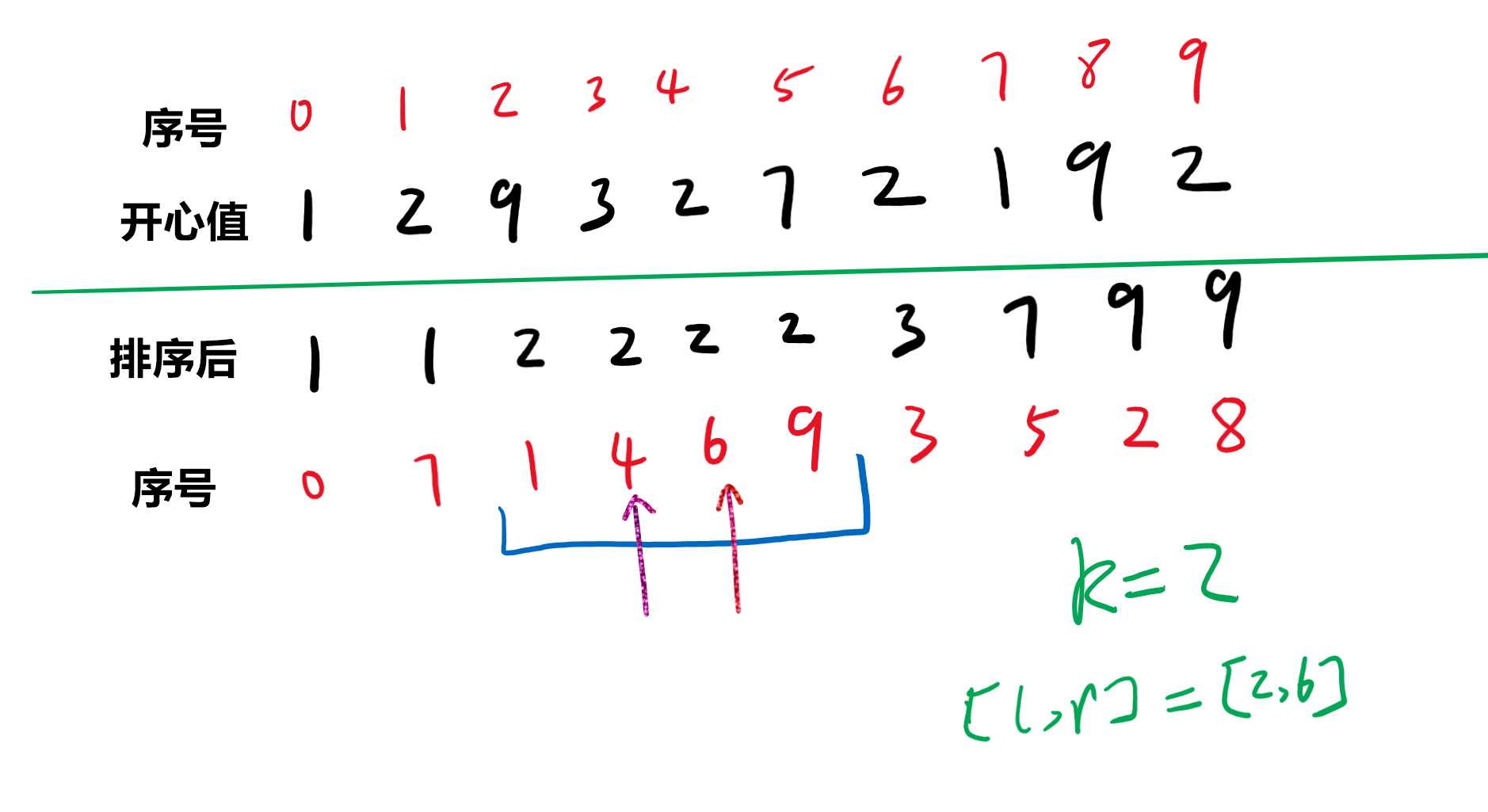
 为了进行二分查找，我们对喜好值进行排序，但是注意到有查询区间，所以标号也必须一起排序。需要注意的是在喜好值相等的片段里标号也要排成递增次序，这个可以写个结构体(记为Num)然后重写比较函数。那么在标号按递增次序后，我们可以发现，如果要查找[2,6]区间里喜好值为2的人数，只需要二分查找k=2,L=2的上界，以及k=2，R=6的下界。

（也可以理解为先二分查找k所在的区间，然后二分查找L和R的位置，然后取其长度，但实际上只需要两次二分查找就行了，毕竟排序函数如果可以用比较函数把数组排好序，那么同样可以只用一次二分查找把边界找出来，因为它们都用到自定义的比较函数）

如图找到下界4和上界6，那么上界与下界之间的长度即为[2,6]之间的喜好值为2的人数，即答案为2。

 

需要用到的是二分查找的函数，这里复习一下：

用lower_bound找到第一个大于或等于左端点的位置，

用upper_bound找到最后一个小于或等于右端点的位置

 

记一次发现：在使用如下比较函数时，用上例查找到的下标为2，4，然后4-2=2，并不是找到3和4的下标。尝试在下标比较后加入等号，然后ansR-ansL+1，但是这样提交的程序是错误的，待发现原因......

 

#include<iostream>
#include<cstdio>
#include<algorithm>
using namespace std;

const int maxn=300000+5;

struct Num{
    int id;
    int val;
     bool operator<(const Num &b)const{
        if(val==b.val)return id<b.id;    //注意，加等号是不对的
        else return val<b.val;
    }
}num[maxn];

int main()
{
    int n;
    scanf("%d",&n);
    for(int i=0;i<n;i++){
        scanf("%d",&num[i].val);
        num[i].id=i;
    }
    sort(num,num+n);
    int q;
    scanf("%d",&q);
    while(q--){
        int l,r,k;
        scanf("%d%d%d",&l,&r,&k);
        l--; r--;
        Num L,R;
        L.id=l;   R.id=r;
        L.val=R.val=k;
        int ansL=lower_bound(num,num+n,L)-num;
        int ansR=upper_bound(num,num+n,R)-num;
        printf("%d\n",ansR-ansL);
    }

    return 0;
}